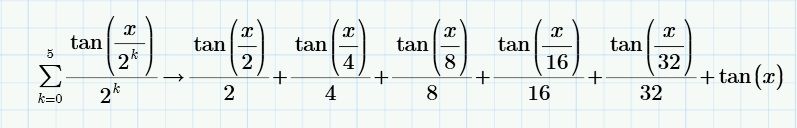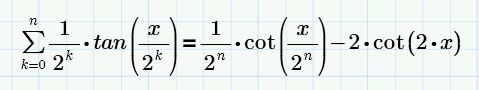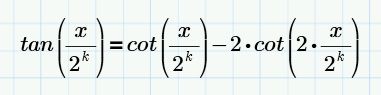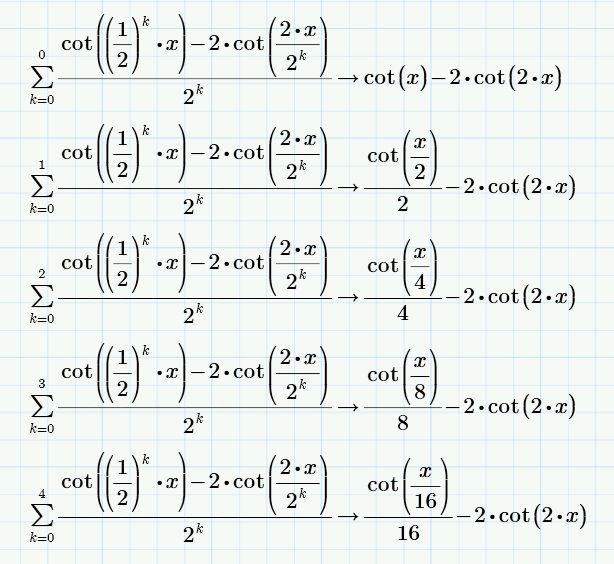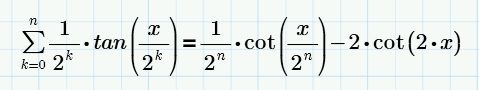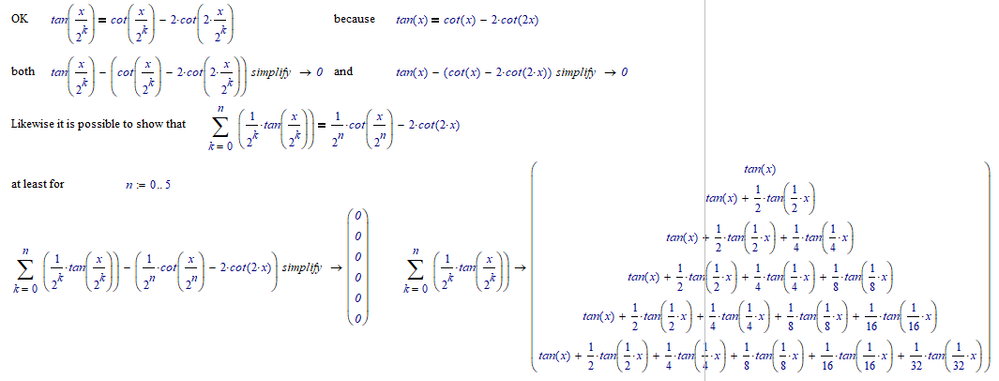Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Help with symbolic calculation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Help with symbolic calculation
I have tried to solve this summation with symbolic calculation but it does not give me an answer:
If I give a value to n, I get an answer:
Which keyword or modifier should I use to get a response without giving a numeric value to n??
Would appreciate any help to solve this problem.
Solved! Go to Solution.
- Labels:
-
Other
- Tags:
- calculation
- symbolic
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
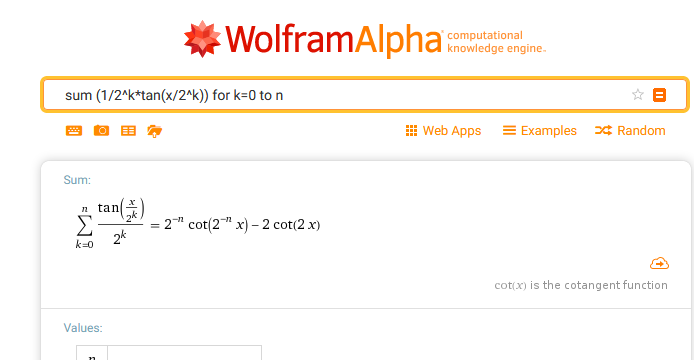
Yes, the simplification is correct but Mathcad's abilities are unfortunately very limited when it comes to symbolic calculations. Especially when compared to more advanced systems like Mathematica or Maple or even whem compared to Uncle Wolfram (limited mathematica engine):
I am surprised that even Luc did not succeed as he is using mathcad 11 which includes an older version of Maple to do the symbolic calculations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What would you want the solver to show for the generic n? This?
tan(x) + tan(x/2)/2 + tan(x/4)/4 + tan(x/8)/8 + ... + tan(x/2^n)/2^n
This is beter shown with the sigma summation -- as in the original equation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're right, but what I want is to come up with a simplified summation result like this:
For this I manually use this property:
How can I implement it to get the desired result??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm afraid you will not succeed.
Where did the summation go to?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
After playing with the two equations provided by rhanet, I believe that the simplification is accurate. I just can't find a way to make Matchad show it. I can't get Mathcad to show that the innequality is true even if I include an assumption that n is an integer >= 0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, the simplification is correct but Mathcad's abilities are unfortunately very limited when it comes to symbolic calculations. Especially when compared to more advanced systems like Mathematica or Maple or even whem compared to Uncle Wolfram (limited mathematica engine):
I am surprised that even Luc did not succeed as he is using mathcad 11 which includes an older version of Maple to do the symbolic calculations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I arrive at the answer giving values to n:
generalizing we have:
As werner says I will have to go to other programs to do this kind of symbolic calculations.
Thanks for the help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah, while the old Mathcad is in many ways more powerful than its successors, it has its limitations.
Exploring a little further:
Apparently the Maple engine runs astray for n=6, but a step-by-step analysis shows it stil should be able to arrive at the correct answers.
What exactly goes wrong for n= 6 and higher eludes me.
Luc