Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to draw a triangle...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to draw a triangle...
Hello everyone,
Someone knows a smarter way to draw an equilateral triangle?
Thank you very much.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, so the goal is not (or not only) drawing, but rather ....??
Do you need a function of some kind which also gives you any point on the sides of the triangle, not just the vertices? Or is Luc's approach already doing what you have in mind?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh! yes nice,
but my version considers the height of the triangle, changing which, for example, I get an isosceles triangle. however, the use of other geometric figures to build the triangle is not welcome.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
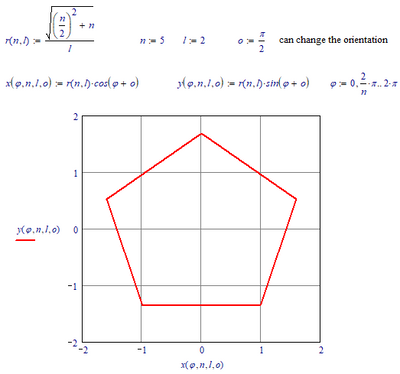
The general case, for an n-angle and orientation o, is:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
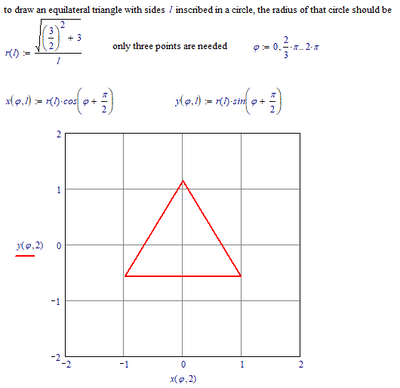
Not sure what exactly you are looking for.
If your goal is to just draw an equilateral triangle dependent on the side length and in the same position in the coordinate system as yours, a simple way would be this:
As Luc wrote, three points are all you need - actually four as you have to duplicate the first one to get a closed figure. You can leave it to Mathcad's 2D plot to connect the points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
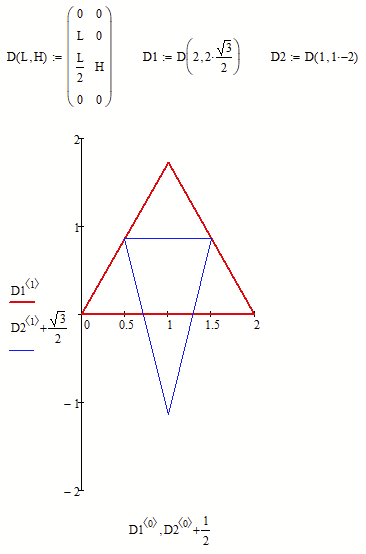
Just read your answer to Luc's post where you say that you also want to draw isosceles triangles depending on the base length and the height.
Here it is:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
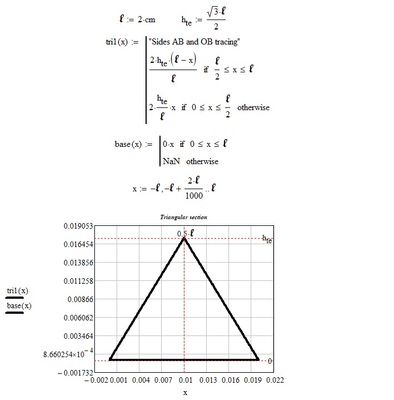
Undoubtedly, I have unclearly posed my question. The fact is that the sides of the triangle are the contour of a hollow metal structure. Within it, there is a physical quantity, solution of a pde, which must vanish on them, so it is not possible to use the matrix, because I can't apply the boundary conditions, even if your solution is very cool.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, so the goal is not (or not only) drawing, but rather ....??
Do you need a function of some kind which also gives you any point on the sides of the triangle, not just the vertices? Or is Luc's approach already doing what you have in mind?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes, that's right, I have to find a function that vanishes on all inner sides of the triangle and satisfies the Helmholtz equation. I think it is beyond your task.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
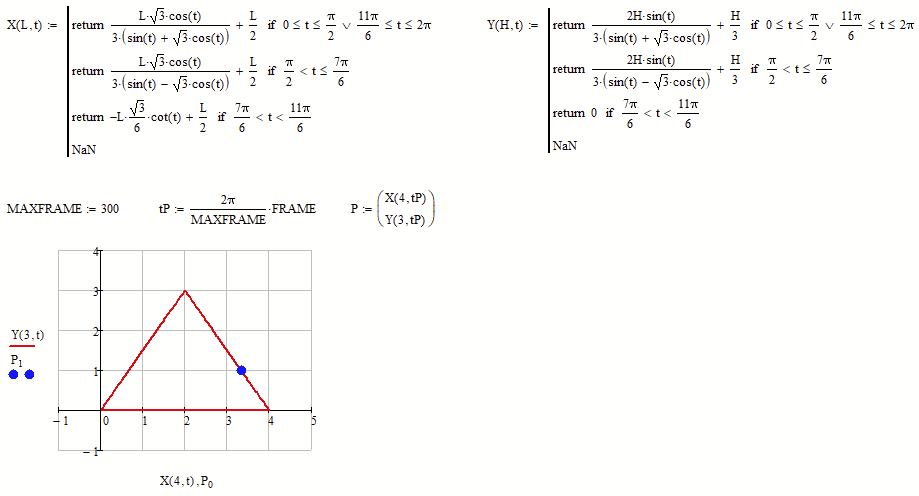
At least here's a parametrized function for the border
And in case Valery is watching ....
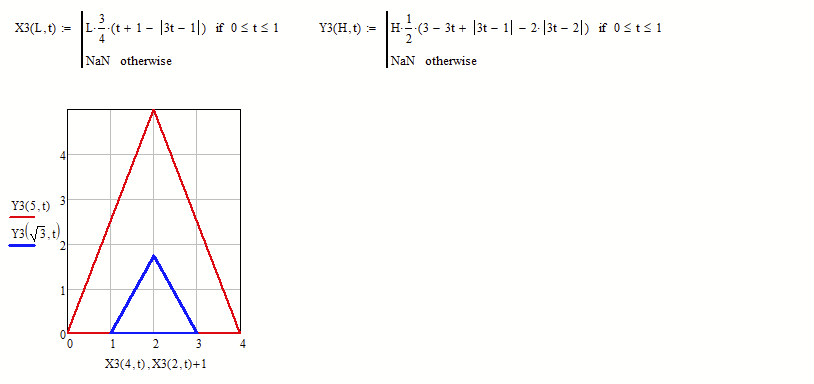
And here a very short parametric representation, using absolute values instead of if-statements:
MC15 file attached