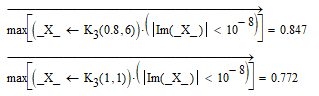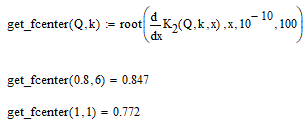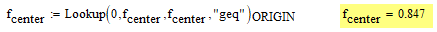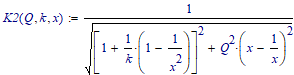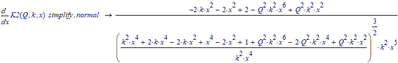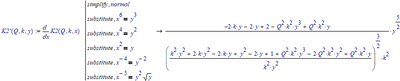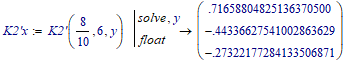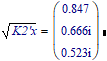- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to only get one value from the answer
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to only get one value from the answer
Hi experts,
I would like to know how to only get one value from my answer.
I mean I only need 0.847, but there are 6 answers in there. does anyone know how to do it.
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
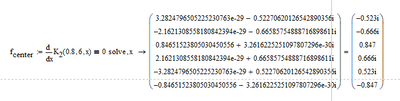
OK. here are two possible solutions to the problem and personally I don't like any of the two.
The first one is based on a strange difference in behaviour between "Lookup" and "Hlookup". I have no idea why "Lookup" returns the non-real values with a positive real part as well, but "Hlookup" only returns the real values.
I don't know if its a bug or if there is a special reason for this difference. But we can take advantage of it and use "Hlookup" to get the largest real solution (and hope that its a positive value, too 😉
Another approach uses the "max" function along with a vectorized evaluation. Because the result vector has to be used twice in this approach and I don't want to call K.3 two times, the function result is stored in a local variable "_X_".
The comparison for "approximate zero" with |....|<10^-8 was necessary because of numerical inaccuracies the real solutions sometimes come along with a very tiny imaginary part.
I guess I already wrote it once or twice that I feel that a pure numeric approach without using the symbolics would be more appropriate and much cleaner and hassle free. I already suggested elsewhere something like
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its always better to attach the worksheet as well, not just a pic.
You may try the modifier "assume" to narrow down the solutions you get. I guess that you are interested in the positive solution only, so you may try "assume,x>0".
Unfortunately the symbolics quite often ignores the"assume" modifier.
You may also consider using one of the two numeric methods. Either a solve block with "find" or one of the two flavors of the "root" function.
Here you can provide an appropriate guess value, add a constraint or provide a range (e.g. from 0 to 5) where Mathcad should look for a solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Simply index the required single answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, terry,
Thanks for your help.
According to your method.
you just need to know where the root is located and then you can use the index to get the answer.
But I would like to use Mathcad to find the positive value in these results, is any possible could do that?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
But I would like to use Mathcad to find the positive value in these results, is any possible could do that?
Use the maximum of real values to get positive result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using max(Re(K.2(Q,k))), how can you be sure that (for different values of Q and k) no non-real solution has a larger real part than the real solution?
Here is an example where the method fails
Possibly k=Q=1 are values which are not of interest or cannot happen in the application @J_power needs the solution for. But then we would need to know which range k and Q can be chosen from and then we would have to prove that in all those cases the non-real solutions always are pure imaginary (real part = 0) or at least have a real part lower than the largest real solution. Nothing that I would like to do.
All I can say is that the equation must have at least one real solution, most of the times even two (one positive, one negative). The reason for this is that the six solutions are the square roots of the roots of a third order equation with real coefficients (so it has at least one real solution, which might be zero).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK. here are two possible solutions to the problem and personally I don't like any of the two.
The first one is based on a strange difference in behaviour between "Lookup" and "Hlookup". I have no idea why "Lookup" returns the non-real values with a positive real part as well, but "Hlookup" only returns the real values.
I don't know if its a bug or if there is a special reason for this difference. But we can take advantage of it and use "Hlookup" to get the largest real solution (and hope that its a positive value, too 😉
Another approach uses the "max" function along with a vectorized evaluation. Because the result vector has to be used twice in this approach and I don't want to call K.3 two times, the function result is stored in a local variable "_X_".
The comparison for "approximate zero" with |....|<10^-8 was necessary because of numerical inaccuracies the real solutions sometimes come along with a very tiny imaginary part.
I guess I already wrote it once or twice that I feel that a pure numeric approach without using the symbolics would be more appropriate and much cleaner and hassle free. I already suggested elsewhere something like
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
Thanks for your answer, it is useful to me.
I prefer to use Hlookup function to get the answer,
by the way, may I know where I can fund the function meaning of Hlookup?
I have never used this before.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
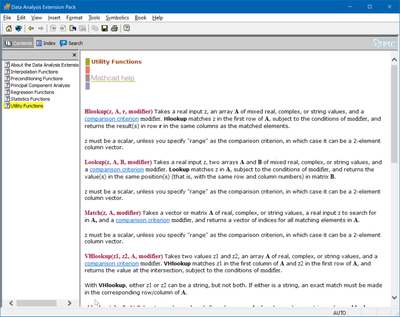
You may just type "Hlookup" anywhere in an empty space (without the quotes) on the worksheet an press F1 while the cursor still is in the just created region. This should fire up the appropriate help page.
The various lookup functions with capital first letter (the ones with a comparison criterion modifier like "geq" are part of the Data Analysis Extension Pack. This was sold separately first but as far as I know the four extension packs were packaged with the main program at no extra costs in version 14 and 15.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hlookup expects vectors as input and if the symbolic thinks there is only one solution, it returns a scalar and not a 1 x 1 matrix (which usually is a good idea).
I already wrote that the "assume" modifier is quite unreliable and I have no idea why "x>0" is not respected with the arguments (0.8, 6) but IS respected with (0.2, 6).
You could work around by using an if statement which return the single value or uses the Hlookup.
Personally I find that the use of the symbolic solve generally is too much of a hassle here.
But it looks like you insist on using the symbolics and do not like my suggestion for a numeric approach using "root".
If symbolics for some reason is a must, my choice still would be
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is another one which does not use the Extension pack function but rather the normal "match" function:
I changed the Zero threshold so we can see that numeric evaluation of K.3 sometimes yields small imaginary parts for what actually should be a pure real number.
Fortunately "match" uses a lower accuracy and assumes those imaginary part as being zero.
We can turn this approach into a compact utility function:
Drawback here is that this function returns the first real value in the vector and does not ensure that this will be a positive value, let alone the largest of all positive values.
Maybe a simple user-written program is more reliable and flexible to change to your needs:
EDIT: Sorry, worked from the sheet @terryhendicott kindly provided but didn't changed its file name.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi @Werner_E,
There are some parts I don't very understand, could you please explain it to me, thanks.
1. Could you please tell me, what R means in your program?
2. Why do you need to use If |Im(Xi)| < 10^-10?
3. What's the purpose of max(R)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@J_power wrote:
Hi @Werner_E,
There are some parts I don't very understand, could you please explain it to me, thanks.
1. Could you please tell me, what R means in your program?
2. Why do you need to use If |Im(Xi)| < 10^-10?
3. What's the purpose of max(R)
1) R is the name of a variable for a vector where I collect the real values of the vector which we get from K.3. "R" like "Result" 😉
2) A real value is a value with the imaginary part being zero, so normally you would write if Im(Xi)=0 ...
But as I had shown, because of numerically inaccuracies the real values actually come out as complex numbers with a very small (about 10^-29) imaginary part and so my program may not pick them as being real numbers. Thats the reason I am not asking if the imaginary part is exactly zero, but rather if its approximately zero. My program considers all complex numbers with an imaginary part in the range from -10^-10 to +10^-10 as being a real number. Thats accomplished by asking if the absolute value of the real part is lower than the (arbitrary) threshold 10^-10.
The get rid of the small imaginary part I use Re(Xi) when I add it to the vector R.
3) At the end of the for loop I have collected all real numbers in the vector R. max(R) choses the largest of all (which hopefully is a positive number as well). In the example given so far, the six values we get from K.3 consist of four non-real numbers and two real numbers (same absolute value, different sign).
If I would not use max(R), the result of the function would be a vector with both real values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
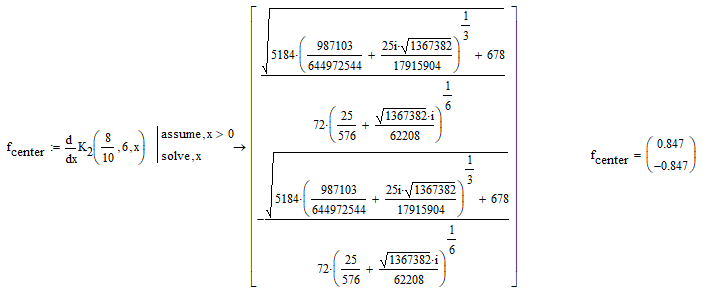
Normally an "assume, x>0" should do the job, but as already written, the symbolics in Mathcad is in no way perfect and ever so often ignores an assume modifier or interprets it not exactly the way we would like it to do.
In your case for some reason we get both real solutions
In case you use the symbolic "solve" on purpose and need the exact expression - you get them if you avoid floating point numbers
If you can't say which element in the result vector is the positive, real value (I guess real and positive are the properties you are interested in), you may let ;Mathcad find the appropriate value for you.
Note the capital "L" in "Lookup" and make "ORIGIN" a vector/matrix index (you may replace it by 0 (zero) if you use Mathcads default values).
But I still think that a pure numeric approach might be more appropriate. See an example here
https://community.ptc.com/t5/Mathcad/Math-equation-solving-problem/m-p/821567/highlight/true#M202440
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You could substitute x^2 for y, like:
Then solve for y:
Now only positive values of K2'x will give you positive roots:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator