How to solve a symbolic equation for vibration system

[sfan]

Hi, friends.

Is there a way to solve the symbolic solution for a vibration system in mathcad?

Such as f(t)=0, and the solution should be in the form of Asin(wt+a)+Bcos(wt+a)

Thank you in advance!

Looking forward to your help!

Shawn

[RichardJ]

Mathcad cannot solve differential equations symbolically.

[sfan]

Hi, Richard,

What if I define the values for these parameters?

say:

m=10, mb=5, E=29000, I=500, L=15.

Is it possible to find the function of v(t)?

Thank you

[RichardJ]

Not using the symbolic processor, no. I don't know if it can be solved using Laplace transforms, it's not something I have any experience with. LucMeekes seems to be kind of a whiz at that though, so maybe he can give an opinion (or, even better, a solution!)

[sfan]

Yeah, I just visit Luc's post, it is fabulous.

Laplace transform works great!

Thank you very much!

[MikeArmstrong]

Please post your solution here to help others.

Mike

[sfan]

Hi, Mike

The attachment is how I used the method of Laplace Transform to solve the equation.

Hope that could help.

Best

Shawn

[LucMeekes]

Hi Shawn,

Good to know that my work is inspiring.

You give:

as the "governing equation", I interpret that as 'the solution'.

For this v(t) it follows that

Much different from the initial conditions that you state:

which are again different from the ones that you actually use:

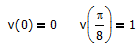
You should get:

The mistake is where you substitute the expression for c into v(t). you're effectively using v(t) - 1 rather than v(t), so you end up with a 'governing equation' for v(t) - 1.

Success!
Luc

[sfan]

Thank you for your correcting.

My work still needs improving.

Your example is really inspiring and you are the best!

BTW, May I ask the reason that you collect the inverse laplace with sin(2t), cos(2t) and exp(t) in this step:

Is it because you found the term on the left side can be traced back to the basic laplace transform like laplace(sinat)= a^2/(s^2+a^2)?

Or collect the inverse laplace with sin(2t), cos(2t) and exp(t) is a universal method in this step?

Thank you for your help!

Shawn

[LucMeekes]

It's certainly not universal (contrary to the formula I use to solve linear differential equations of any order with constant coefficients).

The collection is a remnant of a solution for another problem.

In general the result of the invlaplace is a complicated and 'messy' expression. I usually inspect it to see what are usefull elements to collect. After judiciously choosing the parts for collection the expression often becomes more understandable.

In your case there was a single sine, not with 2t as argument, so the collection didn't do anything.

Success!
Luc

[sfan]

Got ya.

I think it might be better off for me to go review some of the basics of Laplace Transform

before utilize it in Mathcad.

Thank you, man!

[LucMeekes · Accepted solution]

Ah, you wanted the general, symbolic solution. Well here goes:

Success!
Luc

[sfan]

You are my hero, Savvy!