How to solve an equation with a complex variable

[ptc-5989634]

Hi!

How to solve an equation with a complex variable.

G(s):=1/[(s^2)*(s+1)^2]; s- complex variable

like this does not work:

solve,s,assume,s=complex

|G(s)|=1 ----------------------------------------->0.682

with respect Fynjy....

[AlanStevens]

How about:

Alan

[Werner_E]

There is an infinite number of solutions - s=0,682 sure is one of it.

You may try if you get a more general result by adding the modifier "fully"

|G(s)|=1 solve,s,fully --->

[Fred_Kohlhepp]

Interesting!

Version 15 doesn't agree:

[Werner_E]

Fred Kohlhepp wrote:

Interesting!

Version 15 doesn't agree:

Neither do I 😉 It should have been 0.618, not 0.682.

BTW, there is no keyword "complex" in Mathcad 15 and so complex is simply seen as variable. muPad defaults to complex (unfortunately) and we can use something like "assume,x=real" whioch sometimes work as expected and sometimes is ignored.

[Fred_Kohlhepp]

My 15 has "complex" as a Modifier in the symbolic menu block

[Werner_E]

Fred Kohlhepp wrote:

My 15 has "complex" as a Modifier in the symbolic menu block

Mine, too and its also there in Prime 😉

But I think its here for compatibility reasons only and is obsolete otherwise for the reason already written.

But then it should not be treated as a variable and so I had a second look at your sheet. I was wrong about the keyword complex being treated as variable. The reason it was treated that way in your expression was because you used the wrong order. You wrote complex=s instead of s=complex.

Using the correct order we get a funny and absolutely wrong result:

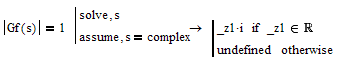
Mathcad claims any multiple of the imaginary unit would be solution.

There seems to be a severe bug in Mathcads symbolics when it comes to the maginitude - see also my last post where I also ran into a bug using the absolute value of a complex.

[ptc-5989634]

MathCad can not solve:

G(x):=1j*x

solve,x

|G(x)|=1-----------> ops!

[Werner_E]

Fynjy Serg wrote:

MathCad can not solve:

G(x):=1j*x

solve,x

|G(x)|=1-----------> ops!

Really??? Are you using a different version? Which?

Here is what Mathcad 15 does for you:

[ptc-5989634]

I use MathCad Prime 3.0

[Werner_E]

The symbolics are the very same in Prime and Mathcad 15, so you should be able to duplicate the solutions shown here. Furthermore, if you buy Prime you get Mathcad 15 along for free. So it may be a good idea to install MC 15 along with Prime - you have to do so anyway if you want to be able to use the worksheet converter.

BTW, it would have been a good idea to state the version you are using in your first post. As you could see many of us use Mathcad 15 (for good reasons).

[AndyWesterman]

Dependant on the constraints that you impose on the values for 's' there may be an infinite number of solutions.

Given that s=a+i*b you have 1 equation & 2 (potentially) independant variables.

In this case, it appears that the solutions all exist on a circular (?) locus (see attached),

but minor changes could give a variety of shapes.

[Werner_E]

Interesting approach. Would n't have thought of a 3D plot.

I also played with the s=a+jb approach and simplified the function, splitting the result in real and imaginary part and solving (magnitude=1) for b in dependence of a. It worked but later I came up with a much simpler way.

Here is a simple way to get "all" solutions to the task and the locus looks like an ellipse, the axis lengths sqrt(5) and sqrt(3).

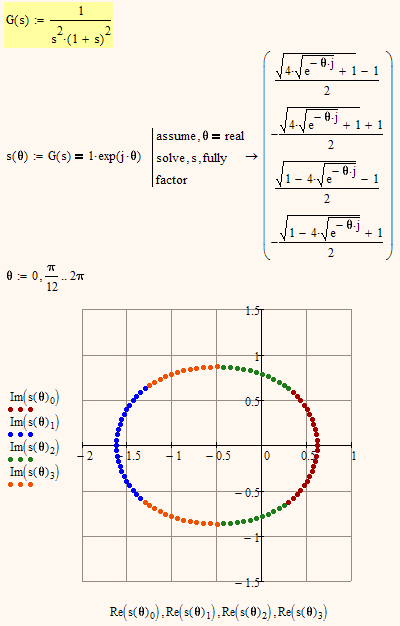
BTW, Alan's solutions are included in this one for theta=0.

[Werner_E]

I send my sheet and also a pdf printout of it as Fynjy Serg wrote he is using Prime (I won't bother converting it).

I also add my first approach with s=a+j*b and I think I ran into a bug of Mathcad's symbolics - take a look:

[ptc-5989634]

Yes.

here's another look.

Let: G(s):=1/[s*(s+1)];

this way he(MathCad Prime 3.0) can:

solve,b,assume,b=real,b>0,float,3

|G(0+1j*b)| =1 ------------------------------------------------------>0.786

but since there is no:

solve,s,assume,Re(s)=0,Im(s)>0,float,3

|G(s)| =1 -------------------------------------------------------------->ops!

although the second method elegant...

[Werner_E]

We already know that Prime is not able to solve that kind of equations, mainly because of the absolute value used I guess. As I showed in my other posts we also get definitely wrong solutions in some cases and the reason seemed to be the absolute value again.

Your initial task seems to be solved though using some different approach.

If the reason of this thread wasn't to find a solution for a concrete problem but to point out that Prime' s symbolics fail in some cases, you should consider opening a support case and turning in a bug report to PTC support staff.