Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
I want to change my work sheet to be fast calculating
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I want to change my work sheet to be fast calculating
my calculation is slow
so I guess it is due to "if" such as upper picture.
How can I change it to be fast?
I attached my file.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is an approach which saves a lot of typing and eliminates all if-statements as well as the definition of the 16 functions. CD1..CD8 and CL1..CL8.

Nevertheless I guess that its not the if-statements and/or the local functions which are responsible for the slowness of those functions. The cause is rather the continuous evaluation of the solve block functions a.r. and a'.r by alpha.r.
I also guess that the solve blocks for a.r and a'.r are wrong as possibly a and a' should be solved for at the same time. As it is set up now, one of them will remain 0. Jinsuk, is this really what is needed that one of those two values is zero and just the other is solved for? In an earlier version you had a solve block I provided which solved for both variables a and a' simultaneously and you changed it now because you got negative values. But what you calculate now is something completely different - you have to know what you really need, so take care!

You define a lot of functions and you nest those functions in an awfully and very inefficient way. For example the function C.P.
C.P calls P,
P calls MO,
MO calls r and m,
m calls v.r, ct, c and r,
v.r calls r, a.r, and a'r,
ct calls Phi.r, CL and CD,
Phi.r calls a.r and a'r,
CL and CD both call alpha.r,
alpha.r calls beta and Phi.r
and Phi.r again calls a.r and a'.r.
Puhh!
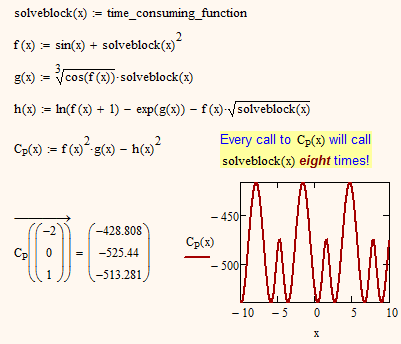
To summarize: One single evaluation of C.P requires eight ![]() times the evaluation of one of the solve blocks (4 time a.r and four times a.r). The interpolating function r is called three time as is Phi.r. If you search for a.r and a'r in one single solve block and rewrite C.P in a more efficient way, you could cut calculation time at least to 1/8. But this would require some bigger changes in your sheet.
times the evaluation of one of the solve blocks (4 time a.r and four times a.r). The interpolating function r is called three time as is Phi.r. If you search for a.r and a'r in one single solve block and rewrite C.P in a more efficient way, you could cut calculation time at least to 1/8. But this would require some bigger changes in your sheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Jinsuk Lee,
I'm assuming that it is the plots that you would like to calculate faster? Without being able to verify that this works since I don't have access to the second Excel spreadsheet referenced in your worksheet, I would suggest changing consecutive "if" statements to "else if" statements. Since each line is an "if" statement, the program must go through each condition, even if the condition is satisfied in the first line. This can waste a lot of time. However, putting "else if" after the initial "if" statement will cause the program to stop evaluating the conditions once it hits a True value.
Hopefully that helps.
Take care,
Luke
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What you say is true, but an even better solution would be to replace all the local function assignments with a return statement, for example "return CL1(x,x,x,x)". The local function assignment is unnecessary overhead, and the return statement will force program exit as soon as a condition is satisfied.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
What you say is true, but an even better solution would be to replace all the local function assignments with a return statement, for example "return CL1(x,x,x,x)". The local function assignment is unnecessary overhead, and the return statement will force program exit as soon as a condition is satisfied.
I did a quick check, just before leaving work a couple of hours ago, on a sort of M14 equivalent and reckon it ll probably double the speed of calling. I also tried putting the functions in an array and using match to locate the index of the appropriate function. Worked out about the same as immediate return.
I suspect that optimising the functions may be more fruitful. However, I don't have Prime so can't confirm this.
Oh, one other thing, Jinsuk, is that it can be a bit dangerous to select for equality on floats. 0.1 = 0.1 is an equality, but k:=0, 0.1 = 0.1*(k+1) is not. This is due to the unavoidable errors introduced by converting 0.1 into an IEEE floating point representation that is actually used for calculations. It's probably fine if you only ever explicitly compare typed in values, but it would be prudent to put an else clause in to trap any calculated cases that aren't quite equal ... or select on a small range around each target value.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I suspect that optimising the functions may be more fruitful. However, I don't have Prime so can't confirm this.
They are fairly basic linterp functions, so not a lot to optimize.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is an approach which saves a lot of typing and eliminates all if-statements as well as the definition of the 16 functions. CD1..CD8 and CL1..CL8.

Nevertheless I guess that its not the if-statements and/or the local functions which are responsible for the slowness of those functions. The cause is rather the continuous evaluation of the solve block functions a.r. and a'.r by alpha.r.
I also guess that the solve blocks for a.r and a'.r are wrong as possibly a and a' should be solved for at the same time. As it is set up now, one of them will remain 0. Jinsuk, is this really what is needed that one of those two values is zero and just the other is solved for? In an earlier version you had a solve block I provided which solved for both variables a and a' simultaneously and you changed it now because you got negative values. But what you calculate now is something completely different - you have to know what you really need, so take care!

You define a lot of functions and you nest those functions in an awfully and very inefficient way. For example the function C.P.
C.P calls P,
P calls MO,
MO calls r and m,
m calls v.r, ct, c and r,
v.r calls r, a.r, and a'r,
ct calls Phi.r, CL and CD,
Phi.r calls a.r and a'r,
CL and CD both call alpha.r,
alpha.r calls beta and Phi.r
and Phi.r again calls a.r and a'.r.
Puhh!
To summarize: One single evaluation of C.P requires eight ![]() times the evaluation of one of the solve blocks (4 time a.r and four times a.r). The interpolating function r is called three time as is Phi.r. If you search for a.r and a'r in one single solve block and rewrite C.P in a more efficient way, you could cut calculation time at least to 1/8. But this would require some bigger changes in your sheet.
times the evaluation of one of the solve blocks (4 time a.r and four times a.r). The interpolating function r is called three time as is Phi.r. If you search for a.r and a'r in one single solve block and rewrite C.P in a more efficient way, you could cut calculation time at least to 1/8. But this would require some bigger changes in your sheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner. Very thank you for helping me.
But I have a question.
You define a lot of functions and you nest those functions in an awfully and very inefficient way.
you said me this sentence.
I need to call many functions because it make me to get C.P..
I know there are many steps to get C.P..
But P is cp(f), MO is f(p)....
it means that they are related to each other.
So In my case, I can' have a choice to avoid calling many fuctions.
Is threre another method to get same result?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jinsuk Lee wrote:
Werner. Very thank you for helping me.
But I have a question.
You define a lot of functions and you nest those functions in an awfully and very inefficient way.
you said me this sentence.
I need to call many functions because it make me to get C.P..
I know there are many steps to get C.P..
But P is cp(f), MO is f(p)....
it means that they are related to each other.
So In my case, I can' have a choice to avoid calling many fuctions.
Is threre another method to get same result?
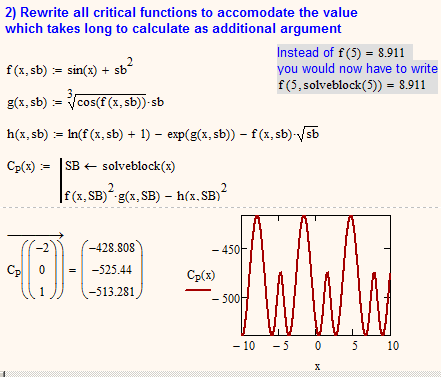
There may be a lot of ways to cope with that problem. See below two different ways to avoid multiple evaluation of a time consuming function but there may be other possibilities.
But before you go into optimizing what you have so far, you sure should make clear what you need concerening a.r and a'r. I don't know anything about the calculations you are doing but its obvious that you are just poking around here and try completetly different calculations. There even might be an alternative way to get those values, maybe even without a time consuming solve block - who knows?
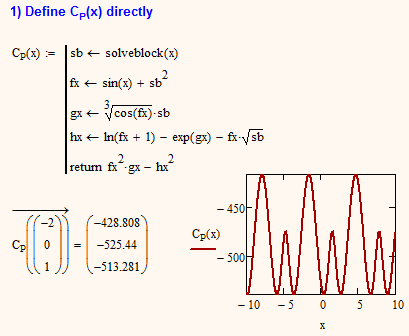
Here is now an example (in MC15) of a function C.P(x) which calls a function I named solveblock(x) eight times and two ways to rewrite the calculations so that C.P(x) does call solveblock(x) only once. Maybe you can get some inspiration from it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello
I want to review about my file.
I tried to change to be fast by using 1 method<Define directly>
I changed almost my file.
But I don't know well it is right. so I want to get advice
Also After I changed my file, I count time and then the result is 27s.
I was surprised because I heard that "mathlab" just spend time on 2~3s.
so I think my work may be wrong.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, one other thing, Jinsuk, is that it can be a bit dangerous to select for equality on floats. 0.1 = 0.1 is an equality, but k:=0, 0.1 = 0.1*(k+1) is not.
I can't understand. Could you instruct again?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Round-off error in the floating point calculations can make evaluation of algebraic equalities fail. It is a beginner's error in numerical methods to depend on floating point equalities. Instead, use:
|A-B|<margin
where margin is the amount of error in the equality, is the way to test if A is close enough to being equal to B while margin is not 0.
If you want to know more, read http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
"What Every Computer Scientist Should Know About Floating-Point Arithmetic"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
even better solution would be to replace all the local function assignments with a return statement, for example "return CL1(x,x,x,x)".
I can't understand well. could you instruct for me in detail?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you mean that
For exampla
if m=0.1
cl<<<cl1
elese if m=0.2
cl<<<cl2
elese if m=0.3
cl<<<cl3
.....
elese of m=1
cl<<<cl10





