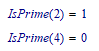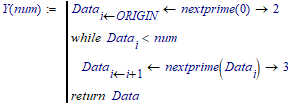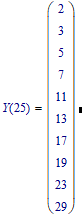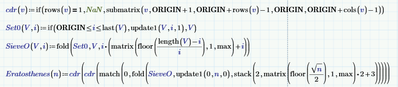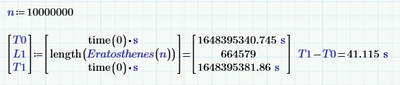Hi
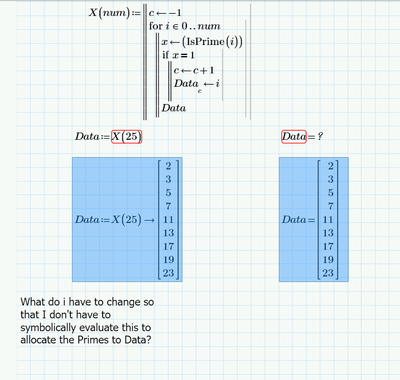
Issue with file as below. Prime 7 attached. I can't allocate the values to "Data" without doing the symbolic evaluation.
1 ACCEPTED SOLUTION
Accepted Solutions
Contrary to Prime, in (real) Mathcad you can make a numeric function IsPrime from the symbolic isprime:
So the function proposed by the OP is possible:
and gives:
There's another function: nextprime that can also be helpful here:
Success!
Luc
Hi,
isPrime() is a symbolic function that can only be used symbolically hence the error message if you try to evaluate it numerically.
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit.
Check this in Wikipedia.
Cheers
Terry
Contrary to Prime, in (real) Mathcad you can make a numeric function IsPrime from the symbolic isprime:
So the function proposed by the OP is possible:
and gives:
There's another function: nextprime that can also be helpful here:
Success!
Luc
As Terry already wrote, IsPrime() is a symbolic only function and so you can't use is with numeric evaluations as you already had experienced. In real Mathcad (MC15 and below) there were tricky ways to pack symbolic evals in a program and so use a symbolic-only function in numeric evaluations, too. But the method wasn't 100% clean and reliable (you may look up the many threads about the LambertW function here in the forum). In Prime those tricks are not working anymore and so I see no way you could use a symbolic-only function with numeric evalution (after all thats what symbolic-only means anyway 😉
So all you can do is do write your own isPrime function. You may create a custom function as described in help here https://support.ptc.com/help/mathcad/r6.0/en/index.html#page/PTC_Mathcad_Help%2Fabout_custom_functions.html
or use Primes programming ability - the latter of course will be working much slower but may be easier to accomplish and share with others.
Here is a basic example of a isPrime function which then is used to create a nextPrime function.
Keep in mind that with numeric evaluation you can't use it for integers with more than 15 digits. The function will fail/give wrong results as you can see in the next screenshot. You could evaluate the function symbolically, too, but it will be very slow so for symbolic eval its sure better to stick with the built-in symbolic-only function.
Your example shows a program which returns all primes up to a given number. You may do without the "x", simply write
if IsPrime(i) .... (no need for =1, too).
But as Terry already wrote, for the task of calculating a list of the first primes, Eratosthenes is sure more efficient.
BTW, this also could be a way to speed-up the isPrime() function: Precalculate all Primes up to 10^6 on top of the worksheet first. Then isPrime could use that list instead of trying every odd number from 3 to the square root. This should make isPrime() work much faster and would accommodate numbers up to 10^12 (=(10^6)^2).
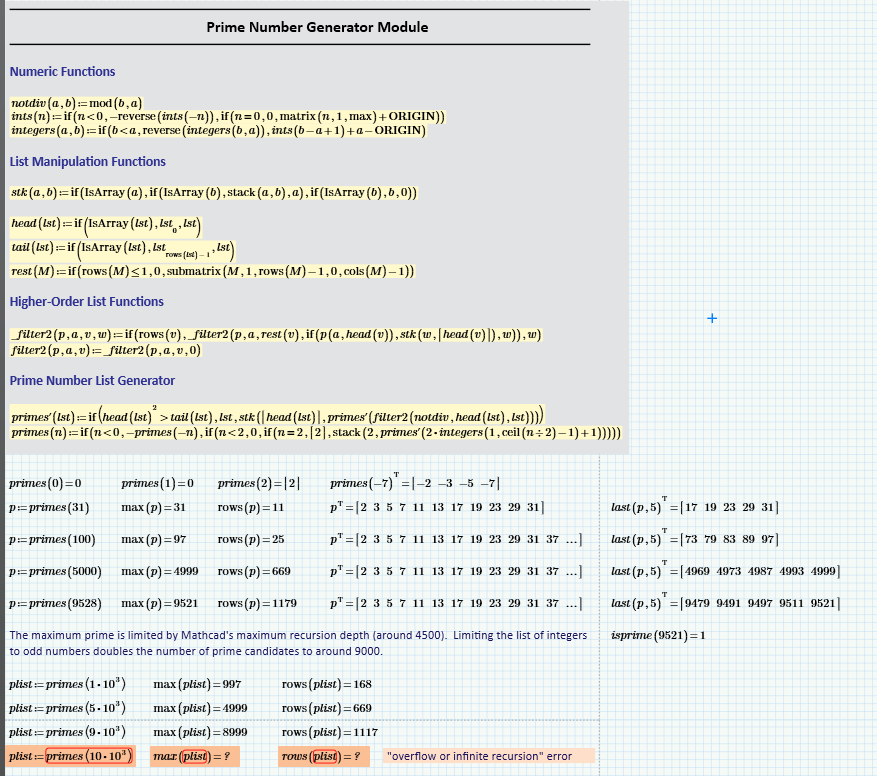
For those of you with only Prime Express, here are a couple of methods of generating prime numbers. I wrote it in Mathcad Prime Express 7, but the attached version is in Mathcad Prime 8 ... unfortunately, I somewhat unthinkingly overwrote the Prime 7 version.
I had a need for some prime numbers but didn't want to spend too much time creating the methods, so it's a bit rough and ready. I'm confident that there are better and more efficient ways to generate primes in Mathcad Express. It takes a looong time to generate a million primes!
Stuart
Here is a programmed sieve (so it won't work in Express) done quite some time ago..
It looks like the many calls to individual functions in EratosthenesO (necessary to do so in PrimeExpress) are quite time consuming:
Clever, I didn't think of using the index as the number. That speeds things up considerably, because it saves me from using the Stacknz() function. I can use match() instead.
Where n=10^7 would take 15 minutes (my PC is a little faster than yours), it's now done within a minute.
But this still uses the full range of n. I'm trying to get it down to just the odd numbers.
Luc
