Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integration as Summation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integration as Summation
Dear All,
I am again coming to you with an issue I have related to work I am doing from a text book this time on the topic of integration as summation. The text book is trying to prove that integration is essentially the summation of an infinite number of rectangles. I have inserted images of the text in question as this is easier (sorry for this being sideways).
The example looks at a simple graph of y=x as seen in the below images. The problem I am having is I understand the concept, indeed I know that to find the area under the line y=x can be derived algebraically by integrating x to give x^2/2 and calculating for x=4 and x=2 and taking one from the other to get an area of 6 units^2.
However, following the example in the text book in the second image I can't see how the penultimate line of lim n to infin 4/n *n + lim n to infin 4/n^2*n(n+1)/2 gives 4 + 2 = 6. I can see that 4/n*n will give 4 as the ns cancel but on the other side I see that 4/n^2*n(n+1)/2 should give 4n^2+n/2n^2 would leave 2+n i.e. the n^2s cancel 4/2 is 2 and there is a remaining n.
I have used Mathcad to confirm my assumptions but Mathcad's symbolics indicate that the top expression in the second image below does give 6 but the bottom expression does not it gives 4 + 2 * lim n to infin n(n+1)/n^2.
Can anyone tell me if I have misunderstood something or if the text book is wrong? I presume this is the former not the latter.
Cheers,
Andy
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
4/n^2*(n*(n+1))/2
how is this simplified to 2?
Its not. As already written above: If you cancel 2 and one n, split it into two fraction and cancel one n again It simplifies to 2/n+2
Its the limit for n->infinity which yields the 2.
(4*n^2+n)/(2*n^2)
Thats wrong! You lost a factor 4 (distributive law!)

It would have been a better idea to cancel before expanding the expression:
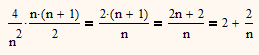
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Notsure which problem you experience.
Maybe you should rather attach your worksheet.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I see what I was doing wrong. I didn't put a * between n and (n and assumed Mathcad would know that n(n+1) meant n * (n+1).
However, can you explain mathematically how this results in 2?
I was of the understanding that n*(n+1) would give n^2+n.
Then 4/n^2 * n^2+n/2 = 4n^2+n/2n^2
Which results in 2+n i.e. 4/2 is 2 and n^2/n^2 is 1?
Where am I going wrong in my understanding?
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> I didn't put a * between n and (n and assumed Mathcad would know that n(n+1) meant n * (n+1).
n(n+1) would mean a function n with argument n+1
> I was of the understanding that n*(n+1) would give n^2+n.
correct!
> Then 4/n^2 * n^2+n/2 = 4n^2+n/2n^2
Oops! You rather should say that 4/n^2 * (n^2+n)/2=2+2/n

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Andy,
your textbook is right.
See attachement please.
What we have here is a gaussian summation:

Hope it helps you
best regards, Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry guys I'm not sure I've explained where I am getting stuck. In the second expression which is simplified to:
4/n^2*(n*(n+1))/2
how is this simplified to 2?
Am I correct in saying this equates to:
(4*n*(n+1))/(2*n^2)
Then
(4*n^2+n)/(2*n^2)
I'm then a bit lost as how this ends in 2?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Andy,
look here:

with n---> infinity you get 2 as result of a limit value.
Am I correct in saying this equates to:
(4*n*(n+1))/(2*n^2)
Yes.
Then
(4*n^2+n)/(2*n^2)
I'm then a bit lost as how this ends in 2?
it's a limit value as said.
regards, Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
4/n^2*(n*(n+1))/2
how is this simplified to 2?
Its not. As already written above: If you cancel 2 and one n, split it into two fraction and cancel one n again It simplifies to 2/n+2
Its the limit for n->infinity which yields the 2.
(4*n^2+n)/(2*n^2)
Thats wrong! You lost a factor 4 (distributive law!)

It would have been a better idea to cancel before expanding the expression:
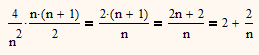
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the penny has dropped.
thanks all!





