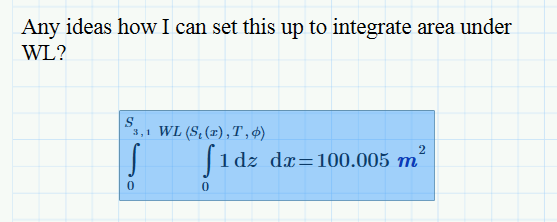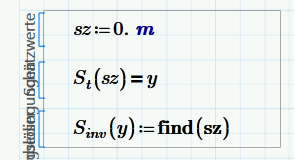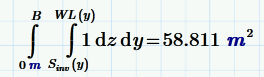Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integration
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integration
Hi to all,
I am further experimenting with my Naval Architecture calculations in MC.
In the attached MCP3 file, can anyone tell me why the integral returns what seems to be an infinite number of answers when the answer I expect to get is 50m^2?
Thanks,
Andy.
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your integral goes to WL(y,T,phi). y is defined as a range variable of 100 points, so it returns 100 results.
Replace y with a single value (5 m or similar) and you get one answer (50 m^2)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Any ideas how I can set this up to integrate area under WL?
As per attached where phi is not 0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
Any ideas how I can set this up to integrate area under WL?
I don't like your setup, but
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Thanks for that. Interested to see what your setup would be.
Also, I think this gives me what I want but am struggling to understand the significance of integrating WL in terms of St is i.e. WL(St(x),T,Phi)? Could you enlighten me?
Thanks,
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Been looking at this further. I think the upper limit of the first integral is going to the upper limit of St(z) i.e. integrating to a height of 20m therefore giving 100m^2 not 50m^2 (assuming Phi is 0)?
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One rule you should consider is NOT TO USE range varaibles for calculations!!
Use ranges for plotting, use ranges for indexing vectors and matrices and uses ranges for loops in a program. But please don't use ranges for anything else unless you really want to run into troubles!!!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I’m still not quite there with a solution though. Ultimately I want to integrate the space inside function St(z) i.e. to the left of the vertical blue line. And up to a height of the function WL(z) ie the black line which may not be horizontal.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
QuoteTop advice Werner. I defined range variables to allow visualisation of the problem.
But you did not leave it at that. The problem in your initial question, the reason you got the strange result which puzzled you, was, that you also used those ranges, which you defined before for plotting, in your calculations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok but if I don't define y the integral returns an error. I have clearly missed the point, can you give me an example of what you mean?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
Ok but if I don't define y the integral returns an error. I have clearly missed the point, can you give me an example of what you mean?
You sure can't use a y in the limits of the outer integral over z. If you expect a numeric result, the limit of the leftmost integral have to be scalars.
Hasn't Fred already shown a possible solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think Fred's solution is exactly what I am after and I am starting to think what I am after is not feasible. It seems that it is not possible to limit the outer integral by a function in the way I want, instead an absolute value or series of values of limits can be used to give the integral for my inner integral to that limit or limits.
Shame, would be really cool if you could limit one integral with another function so as to find the areas/ moments etc of complex shapes.
Cheers,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One way doing it straightforward is by creating the inverse function of S.t
and calculate the area of interest with
If creating the inverse of S.st is not possible because its not a function/not unique, you may consider doing it the other way round. here you would have first calculate the crosssing of S.t and WL to determine the limits of the outer integral (over z) and then use the inverse of WL and S.t as limits for the inner integral over y.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You were correct, I had the wrong limit of integration. The attached MP3 file does what you want (I think).
Werner is right, however, most of us are not used to integrating horizontally. The inner integration can use a function of the outer integration variable as a limit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
HEY!! They fixed it--I could attach the unzipped file!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
You were correct, I had the wrong limit of integration. The attached MP3 file does what you want (I think).
Hmmm, MP3 !? Voice or music? 😉
Oh, its just MC-Prime 3 😞
And yes, they fixed it! Direct attachments of Mathcad files are now possible. It didn't even take a full year to give us back part of what we lost. Great !?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All,
I have been experimenting more and what I have been trying to do I enclose in the attached. I have to give credit to Fred in this as some of what I have done I took from Fred's approach in another thread I had a while ago on a similar subject.
The attachment is the wider problem I have been looking at (for your interest). However, the basic problem is to define the waterline as a programme to either return the waterline or the ship side.
Thanks to all,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All,
I have been experimenting more and what I have been trying to do I enclose in the attached. I have to give credit to Fred in this as some of what I have done I took from Fred's approach in another thread I had a while ago on a similar subject.
The attachment is the wider problem I have been looking at (for your interest). However, the basic problem is to define the waterline as a programme to either return the waterline or the ship side.
Thanks to all,
Andy.