Intervals

[BeNNy]

Hi guys,

today i'm trying to write the ranges within which my variables can move. I want that an angle assumes the value of 0°, and that then it can change between 45° and 100°, for exemple...I state that, being a minimun function, i've just added two test values of these angles...

thank u

[VladimirN]

Can you upload your worksheet?

[BeNNy]

sure

[MikeArmstrong]

Could you please indicate within the sheet where you need help. Users only have limited time to help and scanning through dense sheets takes time.

Mike

[BeNNy]

sorry,

areas in red.

[RichardJ]

I don't understand what you are trying to do. If the angle assumes a value of 0°, then it cannot be between 45° and 100°.

In your constraints the structure x,y is not valid. I'm surprised you don't get an error message. If you remove the "0°,", and the ",180°" to get valid constaints the solution is within the bounds of those constraints.

[BeNNy]

I know that as I wrote it is not correct ... infact I wanted to know how you can write that the angle can be 0 °, or a value between 45 ° and 100 ° (these values are only an exemple) : an interval formed by an isolated value (0°), and a range (45°-100°).... if it is possible of course ...

[RichardJ · Accepted solution]

OK. I see. I don't think it's possible to set a constraint like that. I think you need to solve for the four possible cases:

theta12=0° and theta23=180°

theta12=0° and theta23 varies within a range

theta12 varies within a range and theta23=180°

theta12 and theta23 vary within a range

and then choose the solution from those four that minimizes lambda.

[BeNNy]

Thank you Richard

[AlanStevens]

BeNNy wrote:

.... if it is possible of course ...

I think it's possible - see attached. Whether the results are meaningful is another question entirely!

Alan

[RichardJ]

With your guess values for theta12 and theta23 lambda is not minimized. It's only -0.139, whereas with values of 83.68° and 98.13° lambda is -0.995. If I try starting guesses of 70° and 104°, as in the original worksheet, it fails to converge at all.

Aside from that, I don't think what you are doing can work in practice. The numeric solver just takes small steps, and will not jump between the different cases possible in the "allowed" function.

[AlanStevens]

Richard Jackson wrote:

With your guess values for theta12 and theta23 lambda is not minimized. It's only -0.139, whereas with values of 83.68° and 98.13° lambda is -0.995.

I get -0.138 and -2.825,10^-3 respectively!

If I try starting guesses of 70° and 104°, as in the original worksheet, it fails to converge at all.

Me too. In fact virtually any guess outside the allowed condition fails to converge.

Aside from that, I don't think what you are doing can work in practice. The numeric solver just takes small steps, and will not jump between the different cases possible in the "allowed" function.

I agree this is the likely situation (though it might depend to some extent on the gradients in the lambda function, and on the size of the jumps between the acceptable single value and the acceptable continuous range - which is large in this case).

Alan

[RichardJ]

I get -0.138 and -2.825,10^-3 respectively!

Wow! That is really sensitive to the value of theta23! Try 98.1302°. It's sitting right on the edge of one of those conditional statements higher up the worksheet.

[AlanStevens]

Richard Jackson wrote:

I get -0.138 and -2.825,10^-3 respectively!

Wow! That is really sensitive to the value of theta23! Try 98.1302°

I see what you mean! It's a weird surface!

Technically, 98.1302 is outside the allowed range; upper limit = 98.1301023542

Alan

[AlanStevens]

In fact, if you use 98.1301023542, you also get -0.995, but if you use the even more precise value 98.13010235415 you get -2.825,10^-3 again! I guess we're below the tolerance to which Maximize normally works here though.

Alan

[RichardJ]

Iteresting! Change CTOL to 10^-12 and the solution from the solve block is different.

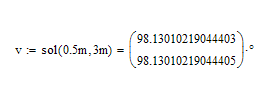
Lambda is then -0.138

[AlanStevens]

In other circumstances, I might attempt to learn the physics of the situation to try to understand what's going on; but there are just too many complicated equations with too little explanation for me to even think about it here! Perhaps BeNNy can shed some light on the situation.

Alan

[RichardJ]

I'm afraid I have too much real (i.e. paid) work to do to spend the time trying to figure it out. There is something strange going on though, because if you increase the upper limit for theta23 by adding 0.001° the two angles drop to about 81.87°. I don't know what physical system this is supposed to represent, but something does not seem right!

[BeNNy]

it is portal masonry subjected to seismic action...i'm attaching the geometry of the problem if you're interested...what's wrong?

[RichardJ]

what's wrong?

I don't know. It's way outside my field. Sorry.