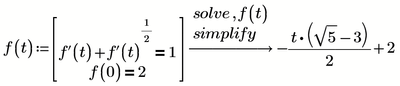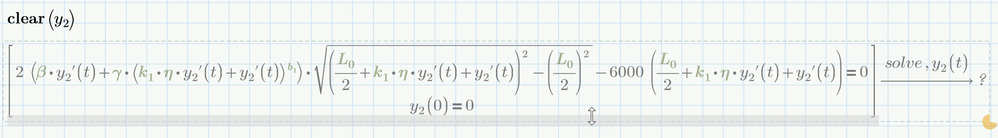Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
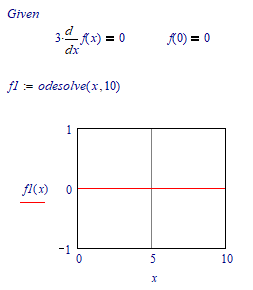
Mathcad Error_Differential Equations_3 types of solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad Error_Differential Equations_3 types of solutions
Hello, Expert guys in this community.
Recently I have received help to solve the problems in using Mathcad Prime 9.0. Appreciate it.
However, since I am just beginner level guy, I am having difficults with ODE solutions.
(In addition, if you can solve those equations with AdamsBDF, then pleas add it)
Please check attached worksheet files.
Your help will be very much appreciated.
Thanks!!
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@주봉_10843142 wrote:
Thanks for the help.
However,if that is the bug, then what I should do about it? 😞
As I had written, it may not be a bug in case of the ODE you provided as the help clearly states that you can only solve ODEs which are linear in the highest order derivative which is not the case in your ODE.
https://support.ptc.com/help/mathcad/r9.0/en/#page/PTC_Mathcad_Help/ode_function.html
I may be wrong and maybe others have some idea to come up with a solution, but I think that unless the symbolic "solve" shown above would finally finish its calculation (I cancelled the operation as it took too long for me) I fear that Prime simply is not able and capable enough to solve your equation 😞
The stand alone solvers like AdamsBDF won't help either as they would require you to explicitly solve the ODE for y2'(t)=....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Method 1:
You have to supply the initial condition for the y2 function INSIDE the solve block, in the 'constraints' part.
Your 'symbols' carry no units, hence y2 cannot use units. The initial condition y2(0*s)=0*m that you state above the solve block uses units...
Method 2: You have no derivative for the function x(t). This might not work with odesolve.
Method 3: F(y) is undefined. In general a constraint for odesolve needs a derivative of the sought function on the left hand segment of a constraint (to the left of =).
I suggest you look up examples of ODE's in the on-line help of Prime.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
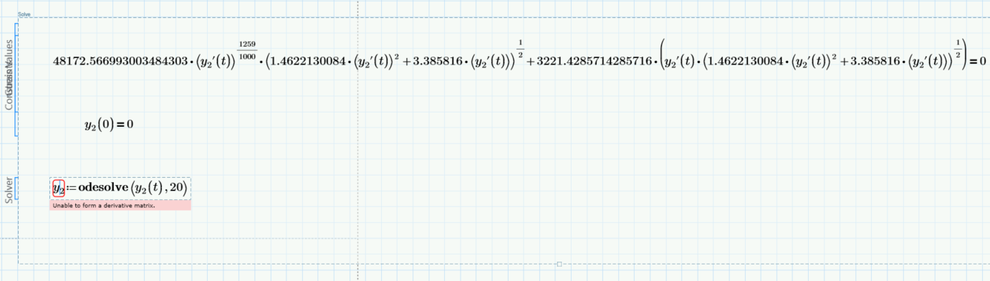
I played around with Method 1 and even by providing a correct IC it did not work.
I guess I tracked it down to a bug in Prime:
Have not succeeded rewriting the ODE in Method 1 so that the bug would not apply
BTW, the bug is already present in Mathcad 15 (error message is "Cannot understand this syntax").
How about MC11 ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11 says:
and:
In other words, Mathcad will not simplify the ODE (collecting identical derivatives to simplify the second ODE to the first) as
optimisation of the ODE cannot be set.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would call this a bug.
And its surprising that its such an old one ...
The error in the OP's sheet may not be called a bug, though, as the help states that odesolve would only solve ODE's which are linear in their highest derivative term which is not the case with the given ODE.
But I think we have already seen ODEs solved correctly which also were not linear wrt the highest derivative - but then I may be wrong, not sure.
As Odesolve fails with an ODE like
but the new symbolic ODE solver succeeds
I gave the ODE in Method1 a try
But the calculation seemed not to finish in finite time, so I had to cancel it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes indeed,,,,I had tried the same way which you showed above....but it seems like a lot of caculation needed (so much computing power required)....so I stopped it.
Whatelse I can do?..... 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think it's not so easy to solve this kind of differential eq...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the help.
However,if that is the bug, then what I should do about it? 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@주봉_10843142 wrote:
Thanks for the help.
However,if that is the bug, then what I should do about it? 😞
As I had written, it may not be a bug in case of the ODE you provided as the help clearly states that you can only solve ODEs which are linear in the highest order derivative which is not the case in your ODE.
https://support.ptc.com/help/mathcad/r9.0/en/#page/PTC_Mathcad_Help/ode_function.html
I may be wrong and maybe others have some idea to come up with a solution, but I think that unless the symbolic "solve" shown above would finally finish its calculation (I cancelled the operation as it took too long for me) I fear that Prime simply is not able and capable enough to solve your equation 😞
The stand alone solvers like AdamsBDF won't help either as they would require you to explicitly solve the ODE for y2'(t)=....