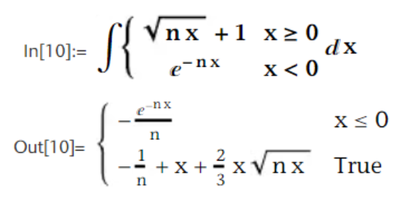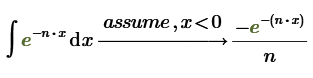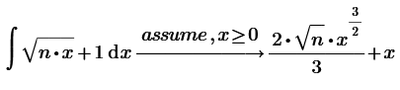Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathcad Prime 8 Wrong integral calculation result? #1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad Prime 8 Wrong integral calculation result? #1
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Cornel wrote:
I think this happens because of that constant which normally is added in the indefinite integral calculation:
Correct. And if a software by default ignores/omits that constant of integration in indefinite integrals, it also should omit that summand 1/n. So Prime is also a bit more "correct" here because its result for this integral also covers correctly the case of n=0 whereas the results of Mathematica is wrong and invalid for n=0.
As for the other integral I am disappointed that neither software considers the case n=0 and simply ignores it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think this happens because of that constant which normally is added in the indefinite integral calculation:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Cornel wrote:
I think this happens because of that constant which normally is added in the indefinite integral calculation:
Correct. And if a software by default ignores/omits that constant of integration in indefinite integrals, it also should omit that summand 1/n. So Prime is also a bit more "correct" here because its result for this integral also covers correctly the case of n=0 whereas the results of Mathematica is wrong and invalid for n=0.
As for the other integral I am disappointed that neither software considers the case n=0 and simply ignores it!