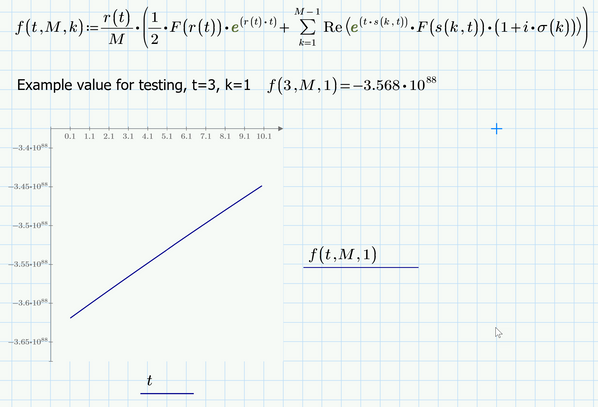
You can't numerically evaluate a function definition, so you must delete the equal sign after the definition of function f.
But there are a couple of other errors, too.
You define r as a function of t and so whenever you use r later, you have to type r(t) and not just r. Same applies to function theta(k).
Therefore your function s(theta) must be a function s(k,t) because its definition uses r(t) and theta(k) and whenever you use s later you have to type s(k,t).
At the end you would have a function f dependent on t, M and and so far undefined value k.
I changed the definitions accordingly but am pretty sure that the result is not what you intended
BTW, you probably know that the imaginary unit is already predefined in Prime. You can type 1i or 1j (without a space or multiplication dot inbetween. For results you have the option to display it either with i or with j (or in polar representation). unfortunately unlike real Mathcad, Prime does not hide the the leading 1 and so the display is rather ugly and unusual which probably is the reason you (re)defined i. You may consider to label it as constant so it looks a bit different from a normal variable.
I couldn't understand the Mathematica syntax in the article you quote. Found another article by the same author and came up with this.
Prime 4 file attached.
Success!
Luc
