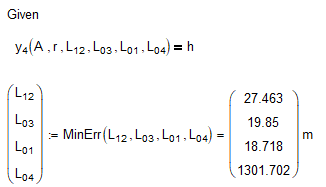Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Minimize or MinErr
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Minimize or MinErr
I would like to solve this problem
https://community.ptc.com/t5/PTC-Mathcad-Questions/Chebyshev-step-macine-optimization/m-p/500155
not with the Minimize function but with the MinErr function.
But do not know how.
Help me please!
The Mathcad 15 and Prime 4 files are in attach.
- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Whats wrong with minimize?
Anyway, here is the simplest way of doing it with minerr (you'll have to chose Quasi-Newton as algorithm to get the very same results as with minimze):
BTW, it looks like you are using a 4K display like me. Pictures you grab from hat screen are far to large to be inserted here, making the threads hard to read. You should either resize the pics before posting or choose "medium" as size when you insert them in a thread.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just gave it a try in Prime4
You have no choice of algorithm
Calculation with minerr takes "endless" time
Result is not as good as the one derived with minimize
Facit: Avoid using Prime whenever possible (and its always possible to avoid).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner!
But I think about this method
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I had not looked in your sheet and your equations in more detail and simply solved with minerr what you had solved with minimize.
You new approach seems to be different as you now have a constant h.
Why aren't you happy with your minimize results?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner!
I see it too!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
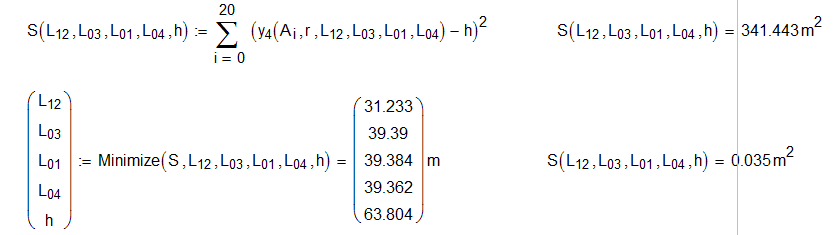

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
S=?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You defined S as the error function, so minimizing it gave your answers.
Find and Minerr act to satisfy constraints, so finding the minimum error for y(...) = h has the same effect.
Note that Minerr is basically Find where Find can't arrive at an acceptable solution. It's always wise to find out how bad your "minimum error" is, it can be quite unacceptable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
wrote:
S=?
Freds approach is basically the same as mine. So the result depends on the algorithm chosen (if you use real Mathcad and not Prime). From the values Fred is showing I guess he did not change the default (Levenberg-Marquardt) which (surprisingly, as LM usally ist best choice) gives a slighty worse result compared to Quasi-Newton or conjugate gradients (which s used by minimize).