Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Need help with symbolic calculation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Need help with symbolic calculation
I have got the solution for the V function, but I cannot have got the solution for the V2 function!
Help please!
The Mathcad Prime 5 sheet in attach!
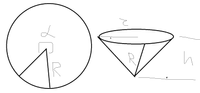
The problem.
We take a round workpiece and cut a sector out of it.
We then fold the cone from the workpiece.
The question is what is value of the cutting angle at which the volume of the cone will be maximum.
I solved the problem with one cone analytically, but I cannot solve it analytically for two cones!
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
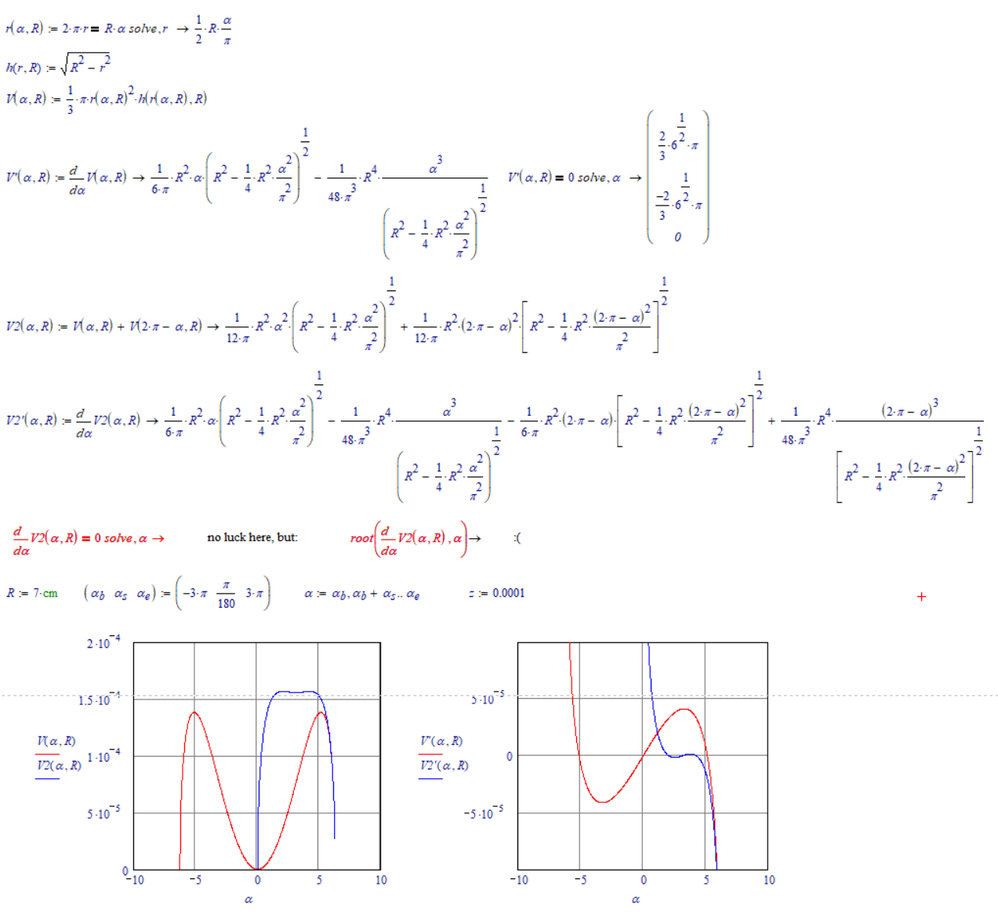
Maybe this helps:
The numeric solve (using root() ) shows one resul that looks very much like it is pi... See attached.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The numeric solve (using root() ) shows one resul that looks very much like it is pi..
For symmetry reasons one solution MUST be exact pi. Unfortunately alpha=pi leads to a local minimum, not a maximum.
Of course the two solutions 2.04 and 4,25 are symmetrical around pi and add up tp 2*pi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
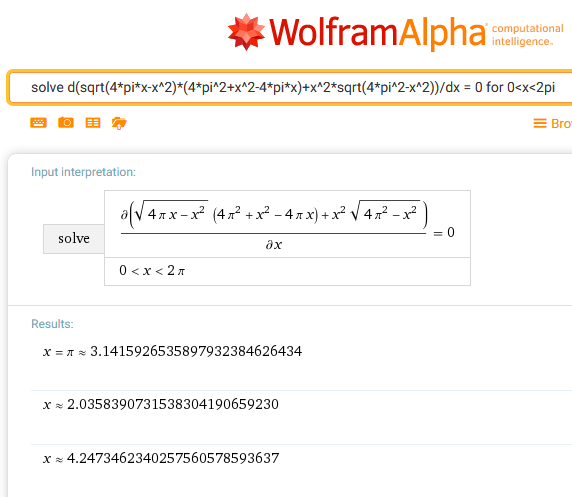
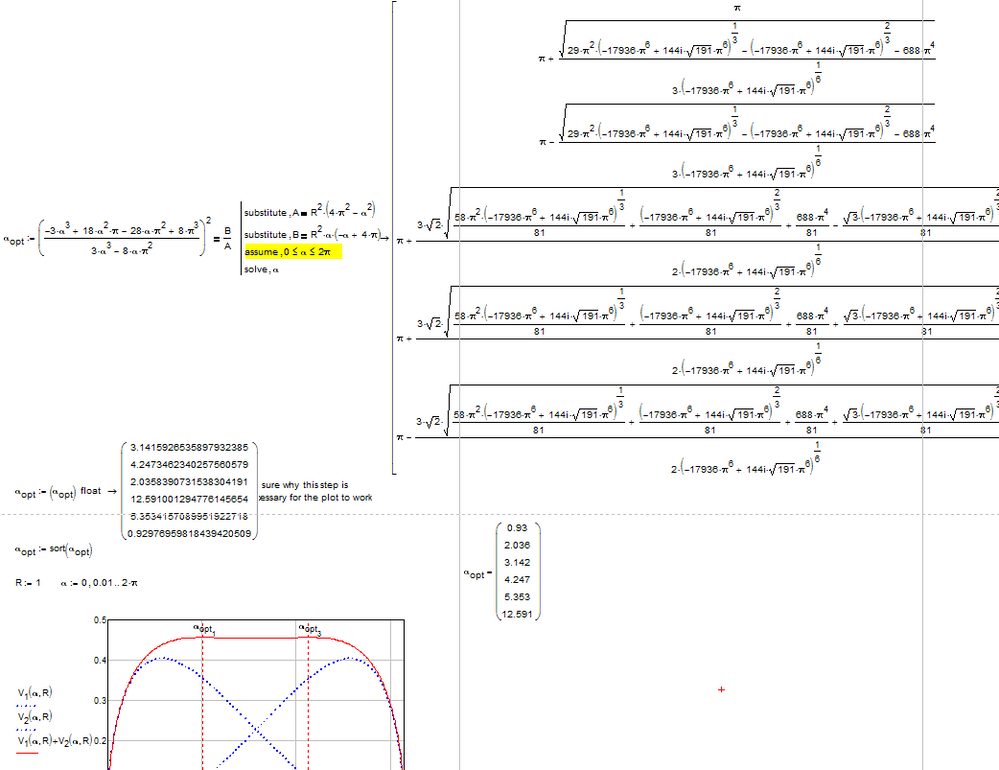
Its too demanding for the symbolics.
Even Wolfram returns a numeric result only (apart from local minimum pi) - at least with just standard computation time:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
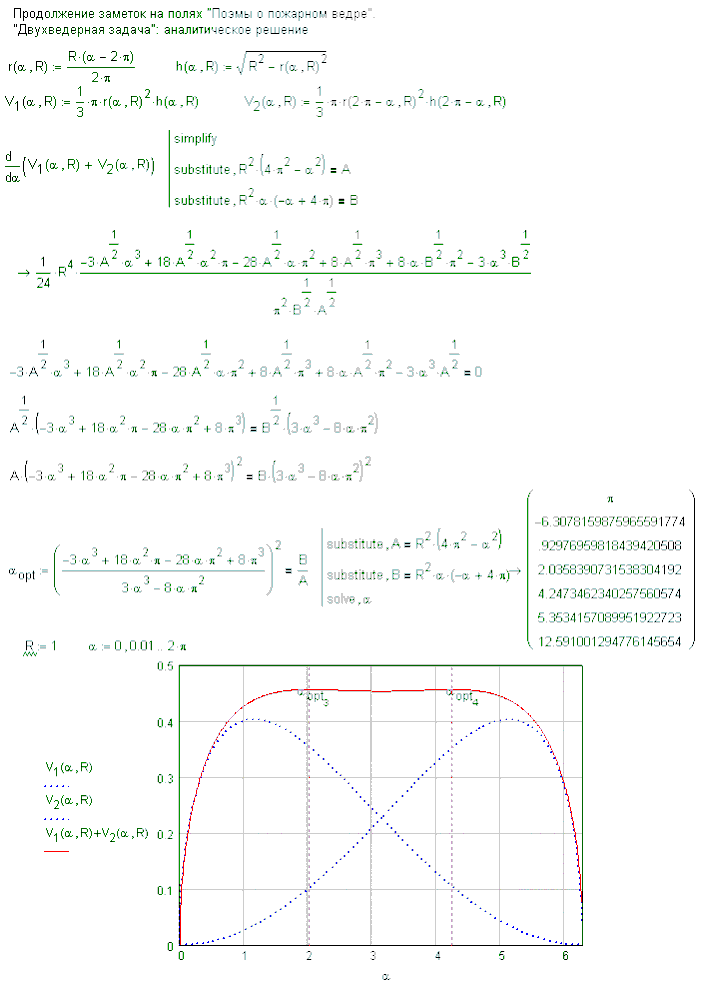
I find old solution from my coauthor Victor Korobov - only Mathcad 11!
Can you do it in Mathcad 15?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
I find old solution from my coauthor Victor Korobov - only Mathcad 11!
Can you do it in Mathcad 15?
Here you are. A simple assume statement does the trick and, Heureka!, you also get the symbolic solution!!!
The assume statement itself is ignored (we also get solutions greater than 2 pi) and there is a somewhat strange behavior of the result when it comes to plotting (using the values for the vertical markers) which makes necessary a redefinition of alpha.opt which I don't understand.