Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Newton-Raphson method
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Newton-Raphson method
Hello everyone,
I am working on a specific case and I have a problem writing the correct code. Let me explain it.
The file is attached. Even though some parameters are red, they are all known. I just had too much data to include in the file, and I just wanted to keep it simple.
My goal is to obtain n1,n2,n3,n4,n5 coefficients, along with T1new, such that f(T) for this T1new will be equal to zero. Moreover, f1,f2,f3,f4,f5 must be equal to zero as well. As a result, I want to achieve such n1-n5 and T1new, that f1-f5 will be zero and f(T1new) will be zero. All other parameters are known. I am not even sure if I am on the right track to find the solution.
Any help would be appreciated.
Regards
Murarz
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Murarz wrote:
Of course, I did not see the post. Let me prepare the file. I had to lock some areas, as it is part of my project and I am not allowed to distribute it.
In one area, which is unclocked, there are definitions of K(T).
OK. I finished doing my other tasks rather later than I hoped, so I haven't checked the attached M15 and MP7 worksheets too closely. I've validated the new Newton-Raphson function against a few examples I found. The solution to your equations doesn't look correct (negative T1). However, the method is sensitive to initial values and it might be worth checking those.
The MP7 version (directly converted from the M15 worksheet and recalculated) isn't showing what I'd expect from Example Three's Jacobian symbolic evaluation. 🤔 I've played around with font, variable names and styles without much luck but it's too far past my bedtime to look at it in any more detail. 😴 It works as I would expect in M15.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Muratz,
Take a look at the finished listing of the program here: https://community.ptc.com/t5/PTC-Mathcad/newton-raphson-method-mathcad-15-HELP/td-p/70305
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Yes, I have seen that post. But it did not help me, that's why I created a new post 😄 The thing is, I am not sure how to include the condition that f1-f5 should be equal to zero by manipulating only n1-n5 parameters. So basically, I want to solve the system of 6 equations and 6 unknows iteratively
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is there a particular reason you are trying to Newton-Raphson? Have you looked at using a Solve block?
Stuart
I don't know if it's applicable to your problem (I haven't had time to look through it properly) but is the following of some potential use?
https://community.ptc.com/t5/PTC-Mathcad/Hooke-Jeeves-function-TOMS178/m-p/65033#M25776
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When applying the given-find method, there there was no solution. That's why I try to solve it differently. The Newton-Raphson method is generally the most common method in solving equilibrium chemical reactions. I will check the link, thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have you tried all methods of the Solve block?
If you press the left-mouse on the find statement you can choose from any of the following methods:
Linear
Nonlinear, either: Conjugate gradient, Levenberg-Marquardt or Quasi-Newton and there are advanced options.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I tried 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Murarz wrote:
When applying the given-find method, there there was no solution. That's why I try to solve it differently. The Newton-Raphson method is generally the most common method in solving equilibrium chemical reactions. I will check the link, thanks
...
<original message>
My goal is to obtain n1,n2,n3,n4,n5 coefficients, along with T1new, such that f(T) for this T1new will be equal to zero. Moreover, f1,f2,f3,f4,f5 must be equal to zero as well. As a result, I want to achieve such n1-n5 and T1new, that f1-f5 will be zero and f(T1new) will be zero.
Hmm. OK. If you're trying to solve for f1..f5 as well, I suggest putting them and f into a vector function of T1 and n1..n5, and trying the NR solver on that. You'll need to calculate the Jacobian, I think.
https://en.wikipedia.org/wiki/Newton%27s_method#Systems_of_equations
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok, I will try this way, thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi!
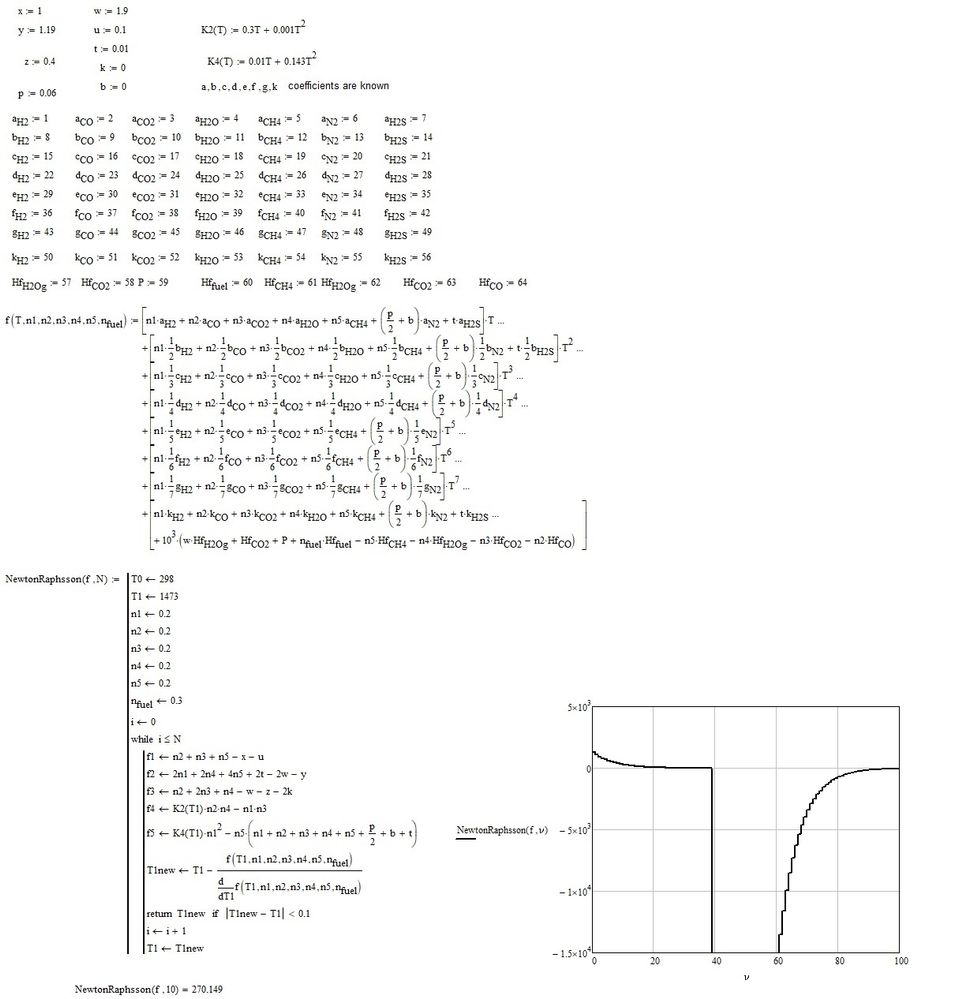
I point out that there are 64 constants to define + nfuel. I have assigned increasing numerical values to which you will then give the actual values. So it turns out:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much for your help. nfuel is a constant as well and it is equal to 1. It seems that there is no stable solution. But I guess this code does not impose a condition that f1-f5 should be zero? Or does it matter in this case? I guess regardless of this additional condition, there will be no solution?
Because the point was to do this procedure iteratively. at first we assume n1-n5, to calculate f1-f5, then, we want such n1-n5 so that f1-f5 will be zero. THen, we calculate the temperature. If the temperature difference between the assumed value and the resultant one is greater than 0.1, then the code takes this newly calculated temperature and repeats the process by calculating again f1-f5 and so on. If the temperature difference is smaller than 0.1, the procedure stops.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Murarz wrote:
Thank you very much for your help. nfuel is a constant as well and it is equal to 1. It seems that there is no stable solution. But I guess this code does not impose a condition that f1-f5 should be zero? Or does it matter in this case? I guess regardless of this additional condition, there will be no solution?
I suspect that the f1..f5 condition is important, hence the suggested vector approach,
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Murarz wrote:
Because the point was to do this procedure iteratively. at first we assume n1-n5, to calculate f1-f5, then, we want such n1-n5 so that f1-f5 will be zero. THen, we calculate the temperature. If the temperature difference between the assumed value and the resultant one is greater than 0.1, then the code takes this newly calculated temperature and repeats the process by calculating again f1-f5 and so on. If the temperature difference is smaller than 0.1, the procedure stops.
The general idea of the system of equations approach is that it is still solved iteratively using a (modified) Newton-Raphson algorithm.
Could you please provide some suitable values to plug into constants in your worksheet? I think I've implemented something that might work but just random values only show that the function is iterating but it's not settling to a solution (which is completely understandable).
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of course, I did not see the post. Let me prepare the file. I had to lock some areas, as it is part of my project and I am not allowed to distribute it.
In one area, which is unclocked, there are definitions of K(T).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Murarz wrote:
Of course, I did not see the post. Let me prepare the file. I had to lock some areas, as it is part of my project and I am not allowed to distribute it.
In one area, which is unclocked, there are definitions of K(T).
OK. I finished doing my other tasks rather later than I hoped, so I haven't checked the attached M15 and MP7 worksheets too closely. I've validated the new Newton-Raphson function against a few examples I found. The solution to your equations doesn't look correct (negative T1). However, the method is sensitive to initial values and it might be worth checking those.
The MP7 version (directly converted from the M15 worksheet and recalculated) isn't showing what I'd expect from Example Three's Jacobian symbolic evaluation. 🤔 I've played around with font, variable names and styles without much luck but it's too far past my bedtime to look at it in any more detail. 😴 It works as I would expect in M15.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
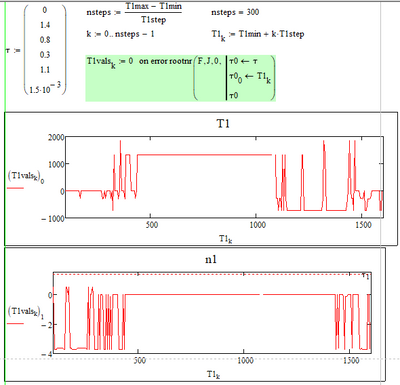
The solution appears to be sensitive to the initial values. Here's a simplistic look at varying T1:
Stuart
(I haven't checked the MP7 version; it's directly converted from the M15 worksheet)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately, given the amount of work you have clearly invested, there is an additional set of constraints.
The variables f1..f5 must also equal zero (see OP original message). These are dependent upon T1 and n1..n5 (plus a number of other variables that appear to be fixed). Consequently, the function to be solved would seem to be a (simultaneous) vector function.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I will try to do that. But one more doubt.
The whole point was to do this procedure iteratively. At first, I want to assume T1 to calculate K2(T1) and K4(T1). Then, by assuming n1-n5, and by having just obtained K2(T1) and K4(T1) I calculate f1-f5. But, I want f1-f5 to be zero. When I have it, then, I calculate the new temperature T1new. If the temperature difference between the assumed value and the resultant one is greater than 0.1, then the code takes this newly calculated temperature and repeats the process by calculating K2(T1new) and K4(T1new), then it calculates again n1-n5 to get f1-f5 equal to zero. Finally, If the temperature difference is smaller than 0.1, the procedure stops. So my question is, does this procedure also require a vector function? Because is a simultaneous solution of k equations the same as solving this in an iterative manner?