Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Numerical issues with Symbolic Derivative Operators
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Numerical issues with Symbolic Derivative Operators
In order to apply the classical Van der Walls Critical Isotherm Conditions to a Carnahan-Staling based EOS, I make use of the derivative operators within a solve block. I found discrepancy between the derivative evaluated by using the symbolic derivative and the expanded derivative ( calculated symbolically ). Furthermore the solve block does not converge with the symbolic derivatives, while it does ( "better" ) with the expanded derivative.
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please post a worksheet showing the problem. It's not possible to give you any kind of answer without a worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the attached worksheet, after the EOS contributions definitions, you could find the isotherm critical conditions non linear system: 1) Non linear system for only dispersion forces EOS using the symbolic derivative; 2) Non linear system including the EOS association contribution ( Wertheim's theory derived ) by using the explicit derivative 3) Non linear system including the EOS association contribution by using the symbolic derivative.
In the second attachment , you could find for instance the procedure for fitting the EOS parameters ( here the explicit derivatives calculated even written a bit differently) for the pure compounds.
in the third attachment, similar procedure for not associating compounds.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Massimiliano Nori wrote:
In the attached worksheet, after the EOS contributions definitions, you could find the isotherm critical conditions non linear system: 1) Non linear system for only dispersion forces EOS using the symbolic derivative; 2) Non linear system including the EOS association contribution ( Wertheim's theory derived ) by using the explicit derivative 3) Non linear system including the EOS association contribution by using the symbolic derivative.
In the second attachment , you could find for instance the procedure for fitting the EOS parameters ( here the explicit derivatives calculated even written a bit differently) for the pure compounds.
in the third attachment, similar procedure for not associating compounds.
Good Morning, Massimiliano
I've just had a look at Benzene.xmcd and there is an undefined variable error where it tries to access an element of the variable Benzene. Where is Benzene defined - I can't see it in the worksheet?

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good Morning, Stuart
Benzene is the table of experimental data. Just before the fitting procedure. On my computer, the file is working properly.
Massimiliano
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Massimiliano Nori wrote:
Good Morning, Stuart
Benzene is the table of experimental data. Just before the fitting procedure. On my computer, the file is working properly.
Massimiliano
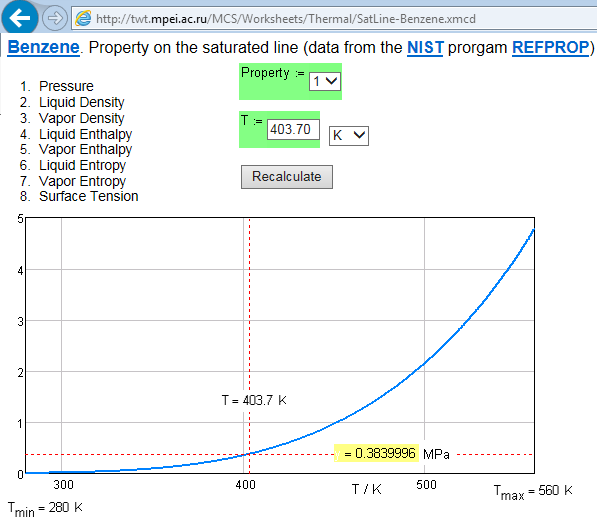
See please this properties on Mathcad Server:
http://twt.mpei.ac.ru/MCS/Worksheets/Thermal/SatLine-Benzene.xmcd
Cloud Mathcad-15 functions are aviable too. And Prime!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Massimiliano Nori wrote:
Good Morning, Stuart
Benzene is the table of experimental data. Just before the fitting procedure. On my computer, the file is working properly.
Massimiliano
Hmm. Interesting. There's just a large blank area on my copy, between "Experimental Data" and "Fitting Procedure". I've had a look at the xml in Notepad++ and there doesn't appear to be anything there either.
Stuart
(from Benzene.xmcd)
<region region-id="1703" left="72" top="1508.25" width="88.5" height="12" align-x="97.5" align-y="1518" show-border="false" show-highlight="false" is-protected="true" z-order="0" background-color="inherit" tag="">
<text use-page-width="false" push-down="false" lock-width="true">
<p style="Normal" margin-left="inherit" margin-right="inherit" text-indent="inherit" text-align="inherit" list-style-type="inherit" tabs="inherit">Experimental Data</p>
</text>
</region> [There is nothing just here in the xmcd file where I'd expect the data to be]
<region region-id="1870" left="36" top="3177" width="85.5" height="12.75" align-x="48" align-y="3186" show-border="false" show-highlight="false" is-protected="true" z-order="0" background-color="inherit" tag="">
<text use-page-width="false" push-down="false" lock-width="true">
<p style="Normal" margin-left="inherit" margin-right="inherit" text-indent="inherit" text-align="inherit" list-style-type="inherit" tabs="inherit">Fitting Procedure </p>
</text>
</region>
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It opens fine for me. There is a huge matrix where you have a blank region. That matrix does contain some non-ASCII characters, and I wonder if whatever you are using to unzip the file is choking on them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Massimiliano Nori wrote:
In the attached worksheet, after the EOS contributions definitions, you could find the isotherm critical conditions non linear system: 1) Non linear system for only dispersion forces EOS using the symbolic derivative; 2) Non linear system including the EOS association contribution ( Wertheim's theory derived ) by using the explicit derivative 3) Non linear system including the EOS association contribution by using the symbolic derivative.
In the second attachment , you could find for instance the procedure for fitting the EOS parameters ( here the explicit derivatives calculated even written a bit differently) for the pure compounds.
in the third attachment, similar procedure for not associating compounds.
Sorry to be a pain, Massimiliano, but could you please be more precise about where you are seeing the differences and what they are? In the acetic acid worksheet, which seems to run, I couldn't see any symbolic evaluations, just numerical ones, and very few explicit derivatives. As I don't know much about EOS, I'm not sure what I'm supposed to be looking for.
I did symbolically evaluate one of the derivatives, and it gave an answer close to the numeric one (but v e r y s l o w l y).

There is overall good agreement, with the discrepancy not too far out from what I'd expect given that the numerical processor uses at max 80 bits for calculations and the symbolic processor uses arbitrary-length arithmetic (not to mention the difference in algorithms).
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The benzene worksheet opens fine for me, but I agree with Stuart that you need to label clearly in your worksheet where you think the problems are.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The issue is related to the computation of the derivatives ( especially second derivative ) with the derivative operator or by using the functions obtained by differentiation within a solve block.
In the attachment "Numerical Evaluation Derivative", the classical critical isotherm inflection point conditions are solved by using the derivative operators ( non Linear System 3 ) and by the functions obtained by differentiation ( Non Linear System 2, so in the file Acetic and benzene ).
For given values of the associating parameters ( epsilonaa=4.13, Vaa=0.378 ), tolerances and initial values, the Non Linear System 2 converges while the non Linear system3 doesn't. In general by increasing the values of the associating parameters, the Not linear system 3 does not converge.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems to me that system 2 has the symbolic derivatives (the big, ugly expressions in the solve block), and system 3 has the numeric derivatives. If one of those big expressions is supposed to be the symbolic second derivative of the P(), then I would say it's wrong, because when you evaluate the second derivative of P numerically immediately after the solve block you get -1858329505, which is a very long way from zero. I see nothing in any of the worksheets showing how you came up with those big expressions though, so I can't say why they might be wrong.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
It seems to me that system 2 has the symbolic derivatives (the big, ugly expressions in the solve block), and system 3 has the numeric derivatives. If one of those big expressions is supposed to be the symbolic second derivative of the P(), then I would say it's wrong, because when you evaluate the second derivative of P numerically immediately after the solve block you get -1858329505, which is a very long way from zero. I see nothing in any of the worksheets showing how you came up with those big expressions though, so I can't say why they might be wrong.
It looks as though the two expressions are quite close numerically over the range of interest
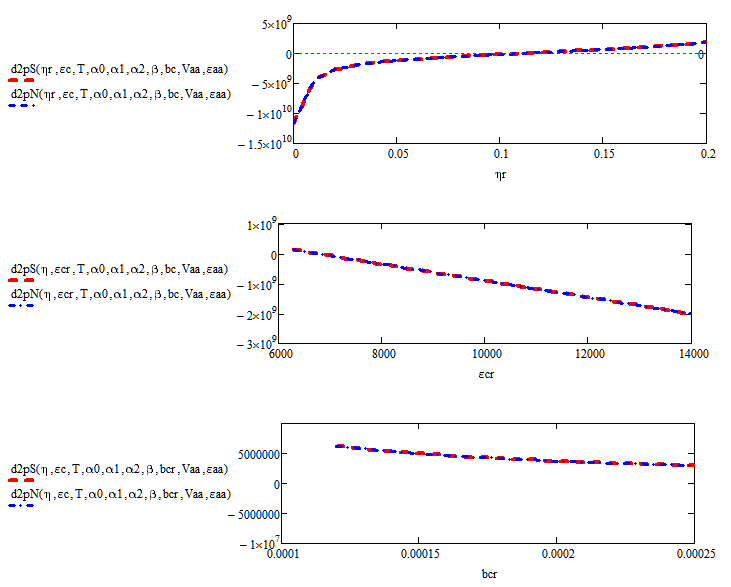
And if I take the delta between the two, it seems quite small

However, the range over which the solve block likely operates has some nasty surprises from a numerical point of view.
ssive
.
Furthermore, given the nature of numerical differentiators and numerical solve blocks, coupled to 80-bit max arithmetic, I'm not at all surprised that Find doesn't work for System 3 ... I'm surprised it gives an answer for System 2, although the fact that it doesn't have to iterate around eta to find the derivative probably helps the solve block keep within a reasonable hypersurface region.
But this didn't explain the discrepancy you saw, as the two functions give almost the same results using the eta, epsilonbc, and bc values from System 2, with the rest having their System 1 values. So I looked at the differences between the other parameters and the difference shows up there. There is a significant difference in the delta function for the values of Vaa given for System 2.
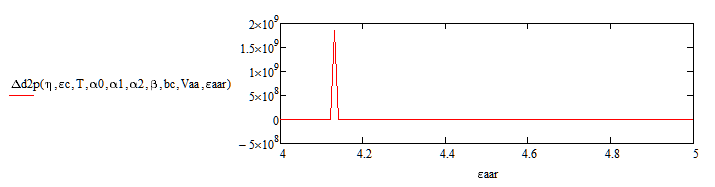
Whether this is down to a genuine difference between the expressions, or to a numerical issue, I don't know. I'm afraid that the pills I'm taking at the moment are giving me a pounding headache, so I'll leave this headache for someone else to look at .... ![]()
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The evaluation of the two functions where you placed them:

The evaluation of the same two functions moved below the system 2 solve block, to the location of the original discrepancy on the right hand page:

At this point, just an observation. More investigation is required.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
The evaluation of the two functions where you placed them:
The evaluation of the same two functions moved below the system 2 solve block, to the location of the original discrepancy on the right hand page:
At this point, just an observation. More investigation is required.
Yes. I think that's because the value of Vaa is different and, as I hint at in my diagrams above, happens to fall at a point where a major discrepancy occurs.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
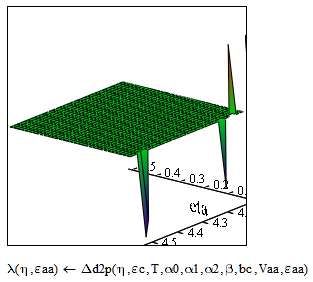
The numeric derivative is really unstable around the solution point:
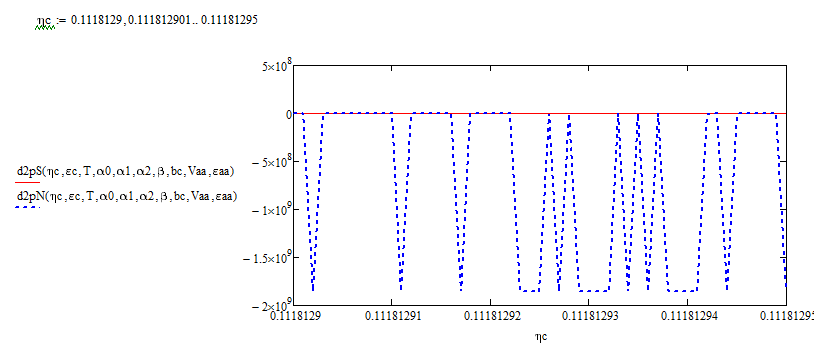
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is very localized:

edit: I tried zooming in on the y-scale of the graph, and Mathcad crashed ![]() . I guess it's time to think about dinner.
. I guess it's time to think about dinner.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Stuart,
have you tried to apply similar analysis to the functions included in Acetic_Acid solve block ? I derived them also from some symbolical expansions in MathCAD.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Massimiliano Nori wrote:
Thank you Stuart,have you tried to apply similar analysis to the functions included in Acetic_Acid solve block ? I derived them also from some symbolical expansions in MathCAD.
I'm afaid I haven't yet looked at the Acetic Acid worksheet; I'll have a look later on.
As an aside, I checked the worksheet in Prime 3.1 and the same numerical issue with the differential operator seems to be present there as well:
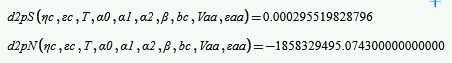
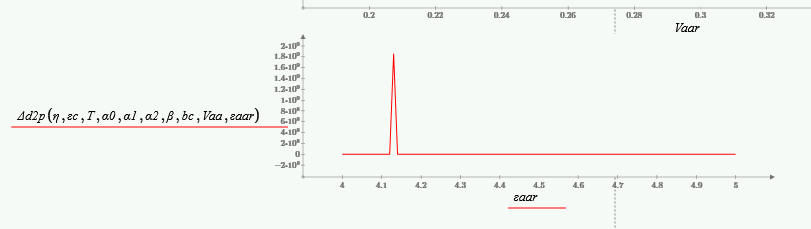
Stuart





