ODE Solvers Won't Solve

[JohnRudnicki]

I have two ode's that have a parameter. When I set the parameter to zero some (but not all) the solvers give results that might be reasonable. But, if I make that parameter a very small number, none of the solvers work even though this would not seem to make the equations parthological. Does anyone have some insight to what is going on?

Thanks.

[VladimirN]

What version of Mathcad are you using?

[JohnRudnicki]

I am using MathCad 14. I post with MathCad 11 so that Luc can help if he wants to.

[LucMeekes]

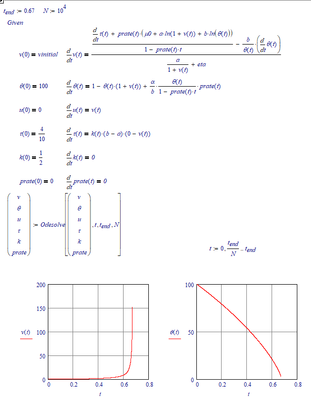
I get to t=0.67. :

for higher values of tend, the error message is: "Found a number with magnitude greater than 10^307 while trying to evaluate this expression". I guess it's related to v(t) running skyhigh

What is the 0 doing in your expression for dTau; should it be Theta? Not that it helps, though: With Theta in that position, I get a solution only up to t=0.1.

Success

[JohnRudnicki]

Hi Luc

Thanks. That was helpful. I anticipated spikes, but not so early. I should have investigated shorter time intervals. With AdamsBDF I get up to 0.8 although all the other solvers fail. Increasing eta which is a kind of damping parameter might help. I haven't looked at this yet but I cannot make it unrealistically large. I do not get a helpful error message like you did. The ones I get are different and less helpful: "this value must be real," "the return value of the function must match the problem size", "this problem does not converge to a solution". A difference between MC 11 and MC 14? I remember that we communicated about this before. 

The zero in dtau should be there. I modified the worksheet from one that looks at a different case. Instead of eliminating the number that went into there, I just made it zero. 

Just case you are interested, the equations describe a spring block model that uses a particular type of friction that has been documented in many experiments on rocks. The friction depends on the velocity v and a state variable theta that reflects the evolving characteristics of the friction surface. The spikes correspond to model earthquakes.

Thanks for taking a look at it.

John