Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
One catenary problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One catenary problem
The description of the problem is here - http://communities.ptc.com/videos/1549#comment-11596
Help me please! My first step is in attach. Is it any right direction?
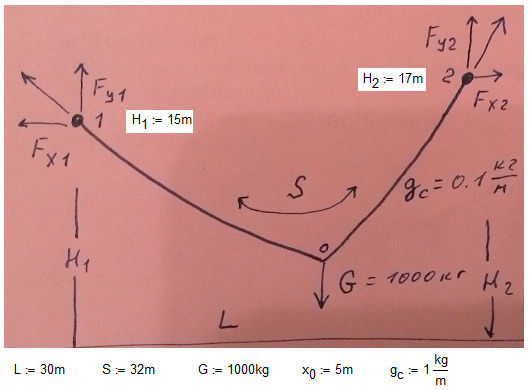
Solved! Go to Solution.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Fred Kohlhepp wrote:
There is nothing so aggravating as a good-looking wrong answer!
The best answer on a good-looking wrong answer is one good-looking correct answer!
Hmmmm! I don't want to be a spoilsport, but ...
1) Are you sure that the chain length is taken in account and dipslayed correctly? Seems to be too long in the graph.
2) With chain weight very low and weight G very high (sheet doesn't allow for anything higher than 10^5) I would have expected approx straight lines.
3) Shouldn't the weight in the middle result in a symmetric solution if H1 = H2?
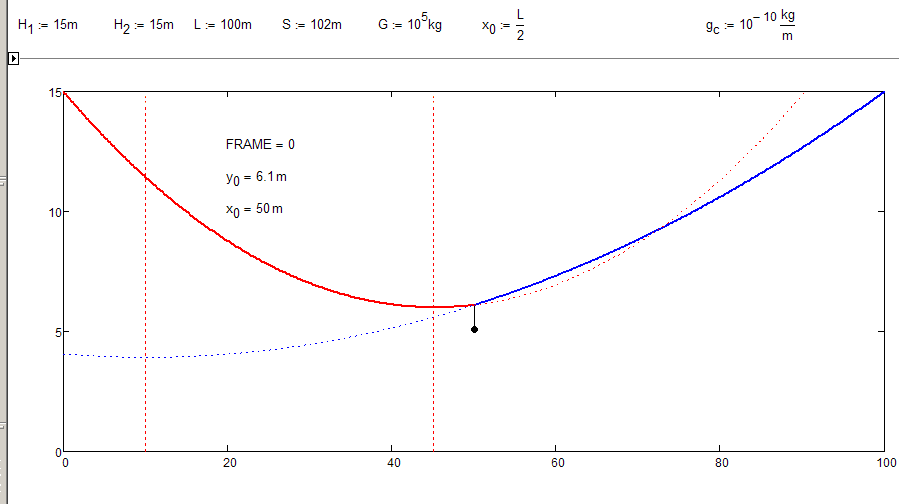
The screenshot is from Valery's latest sheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery Ochkov wrote:
Fred Kohlhepp wrote:
There is nothing so aggravating as a good-looking wrong answer!
The best answer on a good-looking wrong answer is one good-looking correct answer!
3) Shouldn't the weight in the middle result in a symmetric solution if H1 = H2?
The screenshot is from Valery's latest sheet.
Yes, it is not correct. We have (see the attach) 9 unknowns and onli 8 equations. We need one more equation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am still not convinced that the solutions will be ordinary catenaries (proof is still missing) but haven't the time at the moment to model the problem, set up the DE and solve them. Mathcad won't be able to do so anyway (symbolically) but maybe with Mathematica.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Prime 2 (not 3) - see the attach.
(Wi can use units ![]() but cannot use amimation
but cannot use amimation![]() . And we must change y' on dy/dx!!!)
. And we must change y' on dy/dx!!!)

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've come to this rather late so perhaps I'm missing the point, but I don't understand the need to force a particular shape on the chain. Surely its shape will drop out of the analysis? I've produced a discrete mass model (I often find it easier to think discrete rather than continuous!) to illustrate this - see attached. With a relatively small added mass (position marked by red blob in images below) we see a nice curve (well, two nice curves really - one either side of the added mass). With a large added mass it looks quite different.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alan!
The discrete method is a first step to DE.
But can you look my solution and give me one more equation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery tried to model the problem assuming the two curves are still catenaries (I am not that sure about this).
You set x0.1=x0.2 and h.1=h.2.
This is not what was intended. The result is one single catenary without being influenced by G or the forces Fy1 etc (you may even disable those equations).
As I understand it (x0.1 / h1) and (x0.2 / h2) are meant to be the vertices of the two catenaries and so obviosly should not be the same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
I've come to this rather late so perhaps I'm missing the point,
You are maybe coming late but, while numeric and discrete, what you provided seems to be the first correct sheet here. Great work as usual.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner. I'm not surprised I misinterpreted what Valery was trying to achieve as I still can't see why a particular shape function (any shape, catenary or otherwise) is being forced on the curve.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If we knew that the solutions are ordinary catenaries (which in my opinion we don't) Valery's approach would give us the euqations of the curves which seems to be preferred. Nevertheless the coefficients would be calculated just numerically using his solve block. So the next logical step would be to try to find them symbolically. Judging from the equations in use so far I'd guess that Mathcad won't be capable to do so.
IMHO the first step should be to set up the physics to get the differntial equations and solve them. Maybe similar to your discrete appraoch, which in my opinion is surprisingly simple and elegant - I would not have been able to come up with something like that. If possible solve symbolically (probably with the help of Mathematica) so we could see if we arrive at catenaries. If this could be achieved we possibly wouldn't need Valery's solve block at all as we would have a closed symbolic formula for the parameters 😉
But as long as we don't know for sure that the solutions are cateneries ( and I don't claim they aren't, I just doubt it), we should not try hard to find a solution assuming they are. Just my 2 cents.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
If we knew that the solutions are ordinary catenaries (which in my opinion we don't) Valery's approach would give us the euqations of the curves which seems to be preferred. ...
Well, catenaries can be made to fit my discrete model quite well - see below, but I still think it's an unwarranted assumption to make a-priori.
Alan
Edited to correct graphs
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, catenaries can be made to fit my discrete model quite well - see below, but I still think it's an unwarranted assumption to make a-priori.
Thats the point - quite possible that they are catenaries, we simply don't know for sure.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Well, catenaries can be made to fit my discrete model quite well - see below, but I still think it's an unwarranted assumption to make a-priori.
Thats the point - quite possible that they are catenaries, we simply don't know for sure.
Sori Ai du not nou Inglish so gut, bat
Ve hav e chein (цепь) betvin tu (2=1+1) fikset points. It iz e ketaneri (цепь - цепная функция - e^x-e^-x etc) end not moooooooooo nosing. Mey bi Matematica nou more...
In German. Wir haben...
Прошу постить, но мне кажется, может я быть ошибаюсь, но неподвижная цепь, подвешанная между двумя зафиксированными точками, принимает форму цепи (цепной функции с гиперболическим косинусом) и ничего другого...

PS
Alan - it is one Math-gift for you in London in November 2013
And second.
Now I have one English speaker student in MPEI and no problem with Edit my articles.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A catenary is the shape assumed by a member (string, chain, cable) capable of reacting tension but having no flexural stiffness (bends like a noodle.) Derivation of the math for those conditions is readily available, see Wikipedia for example. Werner, you provided a link to a Tom Gutman sheet where he did his usual excellent treatment of the problem.
Since the basic math dereivation of "catenary" is readily available, and since Valery's problem posits that type of member; I believe it's a reasonable assumption that "catenary math" can be used to represent this problem.
I do agree that it needs to be a differential equation solution; most/all of the simple algebraic solutions have either incomplete constructs (mine, where hanging weight mass variations do not alter the shape) or overly simplifying assumptions.
As for a "rigorous proof," I haven't a clue how to satisfy you; perhaps the differential equation solution . . .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Fred!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your interest, Fred, but I have never doubted that the free-hanging chain forms a catenary!
My point is that the single point load changes the physics of the problem and may result in a different solution and so far nobody here has bothered to explain why a catenary should be assumed also for this new problem other than pointing to the classic free hanging chain, which never was doubted to be a catenary.
Can we agree upon that the limit of the analytic solution function(s) for weight G to infinity have to be linear functions? Not just approximately but exactly and independend of the (finite) chainweight.
If yes, then look at the equation of the catenary. The weight G will be present in either a.i, x0.i and h.i or rather all of them. I can't image how the limit g-->infinity would make this equation a linear function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
May I ask what the ultimate purpose of those calculations should be at the end?
I am asking as I am confused about the approach taken. It first seems that a precise analytic solution is what is asked for and then the coefficients of the assumed functions are determined by a numeric approximation (solve block). So if a numeric solution is asked for, why not follow an DE approach similar to what Alan Stevens had done in his discretized approach? Or on the other hand go for an exact symbolic solution, but I think that Mathcad will not be capable enough to do.
As for the discussion concerning the class of function the solution will be of - it won't matter with a DE approach or with a symbolic appraoch you will see by the outcome.
I have a small tendecy to believing to expect catenaries but I agree with Alan Stevens that this is an unwarranted assumption the calculation should not be based on.
On the other hand the argument with the limit G-->inf is convincing on first sight - something I have to think about. At least I would agree that the solustions have to be exact straight lines if the ratio chainweight/pointweight is zero.
I looked at the link to the sheet of Tom Gutman you provided - impressive. I'm not through with it but didn't he solve the very same problem there - including elasticity as it was demanded initially?
Flipping through his sheet I see he is talking about segments of catenaries throughout. But then, I admit I was just cross-reading his document, so I may have missed the point.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
May I ask what the ultimate purpose of those calculations should be at the end?
I am asking as I am confused about the approach taken. It first seems that a precise analytic solution is what is asked for and then the coefficients of the assumed functions are determined by a numeric approximation (solve block). So if a numeric solution is asked for, why not follow an DE approach similar to what Alan Stevens had done in his discretized approach? Or on the other hand go for an exact symbolic solution, but I think that Mathcad will not be capable enough to do.
I appreciate your analysis but can't answer the question about the goal at the end. Maybe Valery can elaborate on this. I agree with your assessment of Mathcad probably not being able to give a symbolic solution. After all Mathcad doesn't provide any means to solve a differential equation symbolically. Best shot would be using Laplace but even this would require manual copy and replace.
I have a small tendecy to believing to expect catenaries but I agree with Alan Stevens that this is an unwarranted assumption the calculation should not be based on.
I am not sure what we should expect, but I sure agree that it would be necessary to agree on the theory of catenary solutions first and the theory should be better secured than just by a good gut feeling. Similar problems may have, but must not have equal solutions.
On the other hand the argument with the limit G-->inf is convincing on first sight - something I have to think about. At least I would agree that the solustions have to be exact straight lines if the ratio chainweight/pointweight is zero.
Yes, taking the ratio makes is more complete, but I wouldn't deal with the case of a weightless chain anyway 😉
I looked at the link to the sheet of Tom Gutman you provided - impressive. I'm not through with it but didn't he solve the very same problem there - including elasticity as it was demanded initially?
Yes, I also wondered what the problem with that sheet may be and why it was considered to be necessary to make a relaunch of the problem. Best guess is that a symbolic solution is targeted.
Flipping through his sheet I see he is talking about segments of catenaries throughout. But then, I admit I was just cross-reading his document, so I may have missed the point.
You are right and if Tom writes something, it sure has weight (an I am not through with his sheet either). But as I read it he is only talking about each individual (infinitesimal) segment being a catenary. His explanation is that the segment is dumb and not able to look beyond its end, so it doesn' know anything about the point load. Tom does not claim that all segments are segments of the very same catenary or that the solution as a whole would be a catenary.
I may compare the problem with that of a suspension bridge with a suspended roadway. As Valery pointed out the segments between the vertical suspension ropes are catenaries, but they arrange in form of a parabola. So again they are not all segments of the same catenary and the overall curve is not a catenary.
Lets stay at the suspension bridge as I just realize that there may be another good comparison to the single point load problem discussed here. Lets make the distance between the vertical ropes infinitesimal small, what curve does the chain form? Most articels will say its a perfect parabola, but thats only true if we neglect the chain/cable weight compared to the weight being supported (which in case of most bridges sure can be done). If the weight of the roadway is zero (hmm?) the chain will form a catenary. So we have (stealing your ratio approach complementing the limes of road or chain to infinity)
ratio chain/Road = 0 ---> parabola
ratio Road/chain = 0 ---> catenary
And inbetween? I don't know, but it will be neither a parabola nor a catenary, I guess.
Back to the single point load:
ratio chain/load = 0 ---> straight lines
ratio load/chain = 0 ---> catenary
In between? Neither the one, nor the other!?
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Seems to be plausible. Think I have to reconsider my tendency for catenaries - looks like the results are something more complex.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Back to the single point load:
ratio chain/load = 0 ---> straight lines
ratio load/chain = 0 ---> catenary
In between? Neither the one, nor the other!?
.
ratio load/chain = 0 ---> catenary
ratio chain/load = 0 ---> straight lines - one limit case of catenary or one limit form of parabola or one limit form of...
What do you prefer?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ratio chain/load = 0 ---> straight lines - one limit case of catenary
Huuuh!?? How would you do THAT? While a polynomial of second order may turn into a linear function, a cosh() never will. Did you read the post? We are talking about perfect straight lines, not just approximations. Or are you just inventing a "new math" only to avoid having to admit to having been wrong? Sorry for sounding harsh but this really isn't helpful at all.
Can you explain what the reason for creating this thread was (other than building an animation).
What specific problem should be solved after you had found the solution (catenary or not)? And why did Tom Gutmans sheet not suffice?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Leopold Turek wrote:
ratio chain/load = 0 ---> straight lines - one limit case of catenaryHuuuh!?? How would you do THAT? While a polynomial of second order may turn into a linear function, a cosh() never will.
Sorry, but we're talking not about a absolute straight line (a linear function). We are talking about a nearly straight line. You can take a rope and strong pull it. You get almost a straight line. But it is (stay be) a catenary!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No,Valery! It looks you are missing the point what a limit is all about. And the formulation using the ratio is even better. if that ratio IS zero your equation must turn into a linear function, not a catenary close to it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
No,Valery! It looks you are missing the point what a limit is all about. And the formulation using the ratio is even better. if that ratio IS zero your equation must turn into a linear function, not a catenary close to it.
OK!
Not
We're talking not about a absolute straight line (a linear function).
But
I am talking not about a absolute straight line (a linear function).
And second.
Show please your animation with correct solution of this task!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If I am convinced or know that a specific way is going in the wrong direction I am usually tempted to warn people following that way. I may know that a way is wrong but this does not necessarily mean I know the right direction. This seems to be the case with the problem here. I have tried to substantiate my position with arguments, but of course everyone is free to simply ignore.
I just hope that Leopold is not correct in his analysis.
So I hope you find soon what you are looking after which seems to be a good looking animation. Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Leopold Turek wrote:
ratio chain/load = 0 ---> straight lines - one limit case of catenary
Can you explain what the reason for creating this thread was (other than building an animation).
What specific problem should be solved after you had found the solution (catenary or not)? And why did Tom Gutmans sheet not suffice?
It all started with animation and animation must end - see one remark here http://communities.ptc.com/videos/1549
I can not use Tom's sheet to create animation.
May be you can?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Leopold Turek wrote:
ratio chain/load = 0 ---> straight lines - one limit case of catenaryHuuuh!?? How would you do THAT? While a polynomial of second order may turn into a linear function, a cosh() never will. Did you read the post? We are talking about perfect straight lines, not just approximations. Or are you just inventing a "new math"
Sorry it is very old math.
We see here not a straight line but a catenary:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Back to the single point load:
ratio chain/load = 0 ---> straight lines
ratio load/chain = 0 ---> catenary
In between? Neither the one, nor the other!?
.
Sorry
not
ratio load/chain = 0 ---> catenary
but
ratio load/chain ---> 0 ---> catenary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Werner Exinger wrote:
Back to the single point load:
ratio chain/load = 0 ---> straight lines
ratio load/chain = 0 ---> catenary
In between? Neither the one, nor the other!?
.
Sorry
not
ratio load/chain = 0 ---> catenary
but
ratio load/chain ---> 0 ---> catenary
Again no, Valery!
It is ratio = 0. This can be either load=0 or lim chain--> infinity.





