Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
One optimization problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One optimization problem
Do you know one symbolic solution of this problem?
See please one numerical solution in attach (M15):
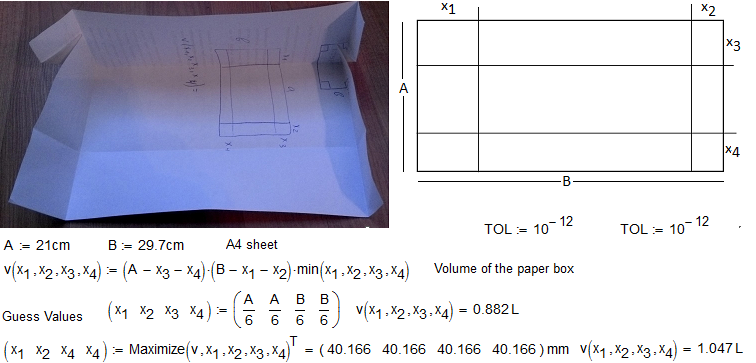
PS At A=B x=A/6
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alan.
To create one program for optimization (Minimize, Maximize etc) - it is one (a little) haft of problem. The second (main) haft is to find functions for the testing of this programs ![]()
I think/hope that my simple function is one good test for it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First guess - x1=x2=x3=x4

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
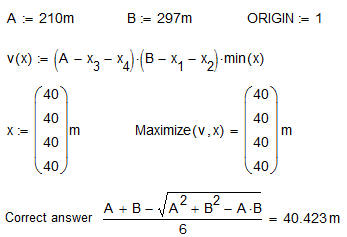
Sorry, I cannot correct solve this problem numerical ![]()
In M15 and P3 - see please the first picture, this picture and attach.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Set up four different variables to solve for: x ... the smallest of the four and you may say its at the side A - that way changing A and B could (not in this case) yield a different result. The other three variables are the differences Delta1 .. Delta3. So wie have V(A,B,x,delta1..delta3):=(A-2x-delta1)*(B-2x-delta2-delta3)*x
That way you get rid of the min() function which is the problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, the system is very sensible with respect to the guess values. Probably a very "flat" function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For the life of me I can't see why you'd want to optimise on four variables here when symmetry dictates that they must all be the same (or, if you prefer, the desire not to waste material means they must all be the same). However, if you insist, here is a way to get the right answer (numerically):
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alan.
To create one program for optimization (Minimize, Maximize etc) - it is one (a little) haft of problem. The second (main) haft is to find functions for the testing of this programs ![]()
I think/hope that my simple function is one good test for it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe I just got a knot in the brain, but shouldn't the four partial derivatives of V() wrt the variables x1..x4 be zero at the solution point? After all its obviously not a boundary value so it wil be a local max.
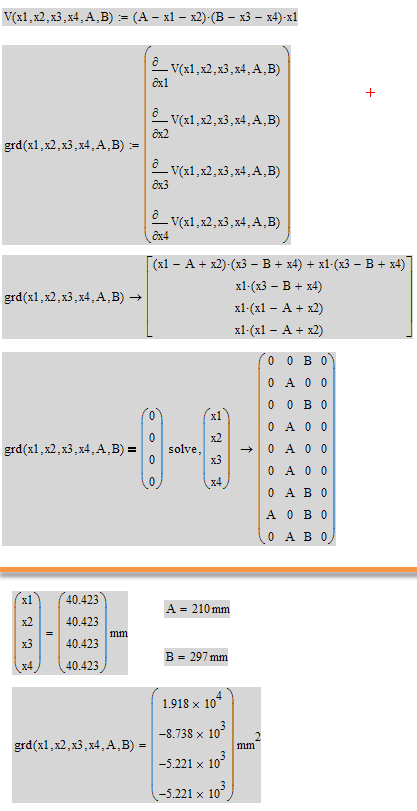
Afterthought: Set up that way its only a problem in three variables, as the only thing the result depends on is the sum of x3 and x4.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice a test problem![]()
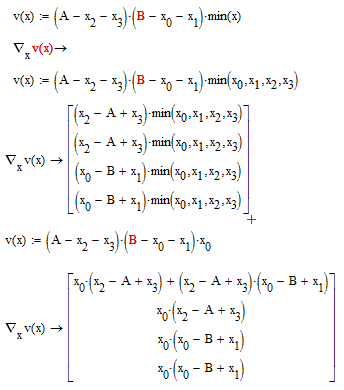
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Nice a test problem

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This shows exactly ... nothing , or?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
This shows exactly ... nothing , or?
Or!
We have a simple function of four arguments with a maximum and can not find direct this maximum with the maximize function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Werner Exinger wrote:
This shows exactly ... nothing , or?
Or!
We have a simple function of four arguments with a maximum and can not find direct this maximum with the maximize function.
Yes, because you didn't constrain.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery Ochkov wrote:
Werner Exinger wrote:
This shows exactly ... nothing , or?
Or!
We have a simple function of four arguments with a maximum and can not find direct this maximum with the maximize function.
Yes, because you didn't constrain.
Can you constrain this problem?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan did
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
????????????
Am I missing the point or is it just playing around w/o deeper insight?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, sometimes I need a little longer to figure it out what is behind a problem.
In case of Valery's 4 variable extreme value problem (which in reality is only a one variable problem) the various objective function would represent a 4dimensional surface in 5-domensional space. This is a little bit difficult for the imagination, so I reduced the problem to just two parameters. I assume that the bent-over lateral surfaces of the box on opposite sides are equal. That way we can visualize the objective functions as 2D-surfaces in 3D space - a bit more comfortable.
The problems that have so far emerged in this thread are:
1) Why does Maximize fail with Valery's objective function using the min() function?
2) Why do the partial derivatives don't evaluate to zero at the solution point
3) Why do we not arrive at the solution by setting the partial derivatives to zero, neither with Valery's, nor with Alan's objective function.
I played around and the attached sheet emerged. As far as I am concerned the answers to the questions are:
1) because min() introduces a discontinuity in the derivation of the objective function, there would not be a unique derivative in the area of the solution and so the CG algorithm, which uses the gradients to approach the solutions, fails
2) & 3) because the solution is not a local maximum of a continous differentiable function.
Any suggestions?
Here the 2D/3D objective functions of Valery and Alan
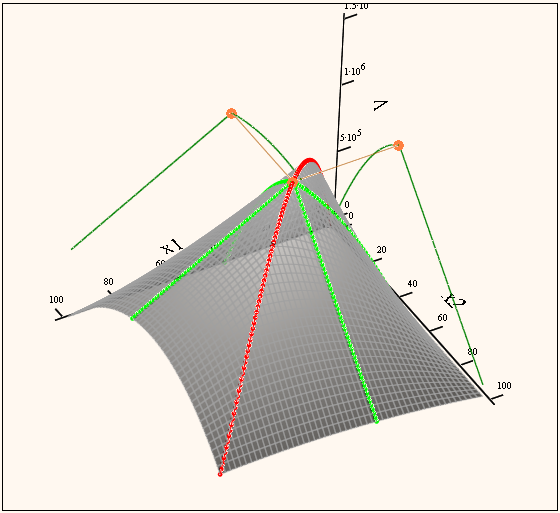
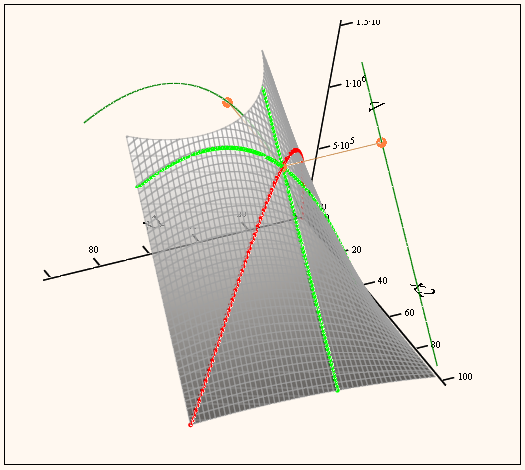
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
2D variant of this problem:
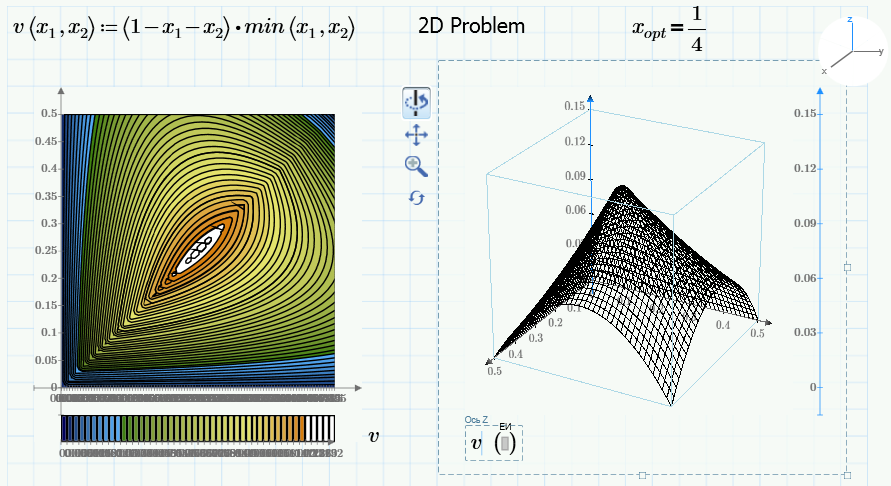
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fractal variant (A=B=1) of this problem - one, five and n boxes from one quadrate sheet:
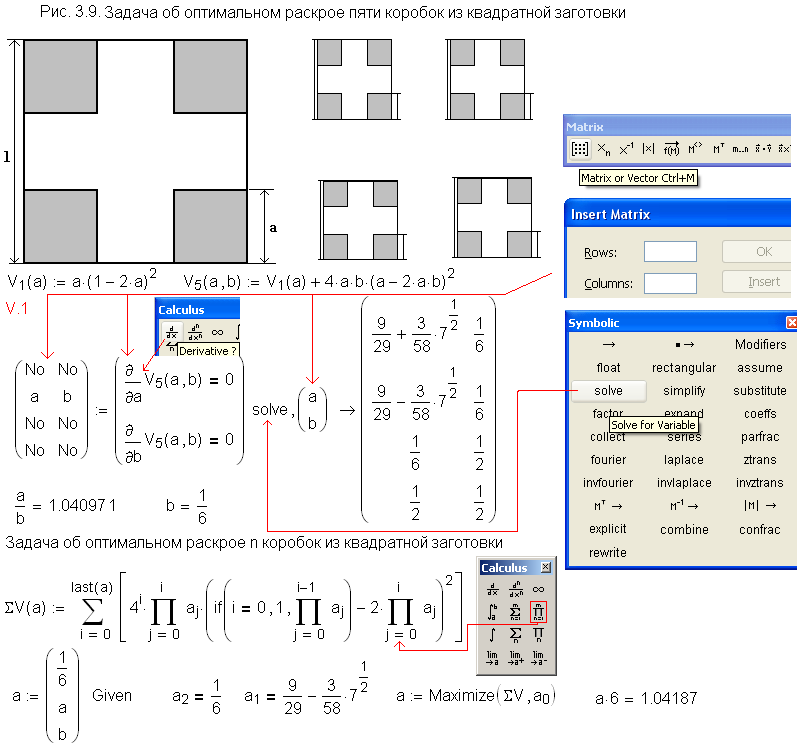
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attached is a simplified version of Valery's box fractal optimisation, but with an infinite number of boxes. It uses only the symbolic maths of Mathcad, not the numerical maths (apart from the graph plots).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
with an infinite number of boxes.
My old solution:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
OK, sometimes I need a little longer to figure it out what is behind a problem.
Thanks, Werner!
See one part of my article "Work on forums - an important aspect of engineering
or
The first step to cloud Universities"
http://twt.mpei.ac.ru/ochkov/CloudUniOchkov.pdf
"Another form of academic work, which is practiced by the author - is hosted lecture material on the forum PlanetPTC for his extensive discussions with fellow teachers from all over the World. One example of such a discussion (one solution to the optimization problem, the comparison of analytical and numerical methods of solution) can be seen here http://communities.ptc.com/message/223224
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
1) Why does Maximize fail with Valery's objective function using the min() function?
Try please this sheet at n>2:
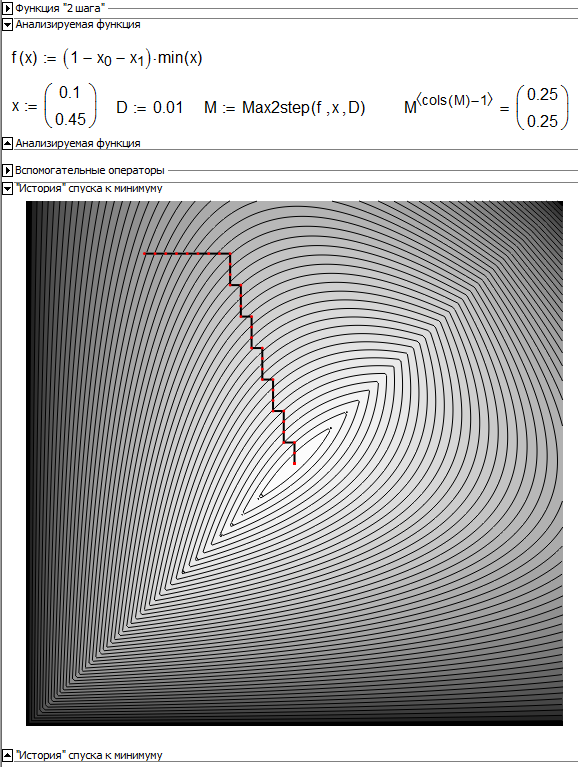
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice, I like it. I am no specialist but the algorithm demonstrated here seems to be neither Conjugate Gradients nor Quasi Newton.
It would be better and informative to trace and graph the behaviour of Mathcad's built-in algorithms - maximize() in our case here. Should not be that difficult to do. We would see that those algorithms are more complex and behave somewhat chaotic and b yno means so "good" and straightforeward as the one we see in your pic.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Nice, I like it.
I am glad.
See please one animation here http://communities.ptc.com/docs/DOC-1979
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How about tracing the algorithm actually used in the problems - Mathcad's built in Maximize()!?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
How about tracing the algorithm actually used in the problems - Mathcad's built in Maximize()!?
See bellow please






