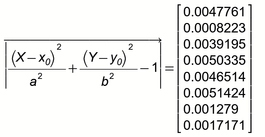Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Oval or Ellipse? It is a question!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oval or Ellipse? It is a question!
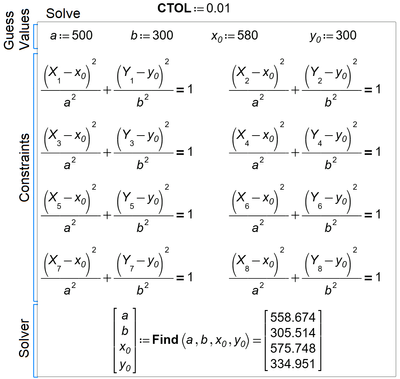
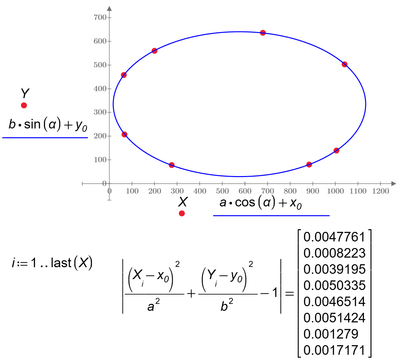
My students and me decided to check which oval Paint draws. It seems to be an ellipse. See pictures below and Prime 6 in attachment.
But there was a suspicion that these are arcs of two pairs of circles - see Oval - Wikipedia.
Problem. There are the coordinates of the four vertices of the "horizontal" oval. It is necessary to draw an ellipse through these points (this problem is solved) and an oval made up of arcs of two pairs of circles. What oval does Paint build? Maybe there is a third way?
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Don't be afraid of using vectors in the solve block (and vectorization when making the check(!
And as its much easier to apply different vertical and horizontal scaling to a circle as opposed to calculating the approximation circle arcs, I would strongly guess that Paint is drawing an ellips and not four approximating circle arcs.
Of course actually its drawing polygons 😉
And given that it cannot create infinite thin line segments and that there is the resolution to be taken in account it actually creates some kind of komplex, filled polygons .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Wener!
@Werner_E wrote:
Don't be afraid of using vectors in the solve block (and vectorization when making the check(!
I have used at first only 4 points and add new and new!
And what about the promlem with 4 circle? I an waiting for the solution!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have used at first only 4 points and add new and new!
One more reason to use the vector equation so you simply can add values in the vectors and the rest remains untouched - no need for a cop and past orgy.
And what about the promlem with 4 circle? I an waiting for the solution!
What will this be good for? It may be a good way to approximate an ellipse when you have to draw it by hand, armed only with ruler and compass. But how would implementing it in a math program make sense??
Of course you could determine center and axis length of the underlying ellipse in a first step (like you already did) and then use appropriate functins to draw the four circle arcs. But again, I can see no reason for doing so.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
„Das Ziel ist nichts, die Bewegung ist alles.“
―Eduard Bernstein
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To be more correct, he said
„Das, was man gemeinhin das sozialistische Endziel nennt, ist mir nichts, die Bewegung alles"
Google transl.: "What is commonly called the socialist end goal is nothing to me, the movement is everything"
Maybe better: "The final goal of socialism is nothing; progress toward that goal is everything."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, "Der Weg ist das Ziel" ["The route is the goal" or "Roads were made for journeys, not destinations", usually attributed to Confucius]
There are many ways to create an oval using four circle arcs as sketched in the link you provided. There is one degree of freedom, so we can introduce one additional parameter. In the ani below this parameter is the radius r1 of the smaller circle in the left figure and a parameter k in the right. The relevant values can be made dependent on multiples of a-b (difference of the half axis) and I named that multiplier k. While r1 may run from 0 to b, k may run from 1 to a/(a-b).
Have fun watching ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The solution with an animation is the solution!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks one more? Werner!
1. Attach please the Mathcad 15 Sheet
2. I think we need to enter into the calculation a certain criterion by which (minimization) you can find an oval, consisting of two pairs of circular arcs, that most closely matches the ellipse. Which?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is the sheet as demanded. Its still a work in progress - no, thats a lie. I don't think that i will revisit it anymore. The routine wont work OK for a<b, so the error checking at the begin would still need some attention. But as I already said - there is not much sense using approximations of that kind in the age of computer programs - and i say that even though I loved drawing quite complex things by hand (and ruined my eyes doing so).
You may play around and find the most appropriate parameter value (possible best done with the "k" variant) depending on a and b.
I vaguely remember learning a quite good approximation construction of an ellipse using touching circles a long time ago, but can't find it. But I guess it wasn't the best solution anyway but rather just an acceptable solution easy to do with compass and ruler.