Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
PDESolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
PDESolve
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>I have posted about this
>before but I think the example
>in the attached worksheet is
>clearer. Compares solution
>from PDESolve to exact
>solution (for a single Fourier
>mode). PDESolve tracks exact
>solution for only a limited
>time range (compare T = 3 and
>4 in worksheet example). Can
>fix this for a particular time
>interval by fiddling with
>number of pts or algorithm,
>but same problem arises if the
>interval is increased (or the
>value of N is changed - Note
>that analytic solution
>increases exponentially if N <<br> >Ncrit ). This is simple linear
>system with an analytic
>solution, but I am really
>interested in a more
>complicated nonlinear system
>(which may also exhibit large
>growth of solutions for
>certain parameter ranges). Is
>there any general guidance
>about how to assess accuracy
>and its domain for PDESolve?
Generally the "large growth" scenarios are a can of worms. But it is an education. Understanding the background to each of the PDE solutions becomes very important. It was only a few years ago that I got a university course on it and it showed just how tricky some of these calculations can be. The algorithm doesn't know in advance what sort of equation it has been given, so you have to choose the algorithm using a little bit of intelligence (i.e. education & knowledge), Or just guess lucky (it can work 😉
Tom is usually very good on these matters
Philip Oakley
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What accuracy ?
The yellow plot are identical, whether num or anal !
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
JmG: Yes, but try increasing T to pi - will see divergence around T = 3. Dont understand why you say top plots have no meaning. They plot the magnitude of the first crest of the sine wave with time. For N > Ncrit, this should decay, which it does for both analy and num, but only in a limited range of T for num.
Bottom plots do track the solution but they are only for relatively small values of T. Everything is nondimensional here - it dont see why T could not be anything positive, including pi/2.
Thanks for the comments.
jwr
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your equations are unstable. You have exponential growth in values. Usually exponential growth in values also means exponential growth in errors. So the inevitable errors (if nothing else, replacing a true value with a representable value, but also the errors implicit in the rather coarse approximations used) grow exponentially, and it becomes just a matter of time before the result is all errors and no signal.
There is something magical about 100 spatial points. Set the time points to 100, and try 99, 100, and 101 spatial points.
__________________
� � � � Tom Gutman
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I dont understand why you say the equations are unstable. They are (grow exponentially) for N < Ncrit, but decay for N > Ncrit (as for the example in the worksheet.) Ncrit is calculated in the worksheet as the value of N at which the real part of the exponential in the solution changes from negative to positive.
Actually I am wondering if the small values of the diffusivities are part of the problem and will take a look at this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And, I dont think the problem was related to small values of the diffusivities (at least directly) as I surmised in the previous post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The PDE is unstable. It is true that the true solution does not necessarily grow exponentially, depending on the parameter N. But N is not a parameter of the actual PDEs (which remain unstable) but rather describe the initial condition. What you have is a PDE where some initial conditions grow without bounds and some decay with time.
But ... the actual initial conditions are never quite as specified. They will always have an error of at least the rounding error due to the limited ability to represent real numbers. This initial error may be small, but een 16 orders of magnitude are easily swallowed up by exponential growth. Further, the calculation is only approximate, so even larger errors will be introduced at each step.
The result is that the actual initial condition, and the result at each time step, will inevitably have spatial frequency components in addition to the single frequency of the analytic solution. Some of these components will have frequencies with N<Ncrit. These components will grow exponentially and eventually completely swamp the nominal solution.
You can delay this by judicious (or lucky) choice of spatial points. 100 seems to be some sort of magic number of this, giving good results out to nearly three. Other values diverge at around two.
__________________
� � � � Tom Gutman
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
==> If the period is T , T = � pi describes the sin ... does it ?
==> the numerical solver discretizes both L & T , the solver take only a little part within a reasonable range. It could be the solver options are underdesigned.
==> The other point is that you plot auto, i.e: under error propagation. The same culprit exists in the rk, well illustrated in the Mathcad 8 work sheet [Steven Finch]. I'm not familiar enough with PDE's to correct or otherwise confirm the way to do..
What I'm saying is that for a unit length L = 1 over T = pi/2 the solver works. If you believe your last "Fourier" plot should decrease exponentially, either the PDE system is incorrect or you have to force the plot to decrease exponentially.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>I don't see why T could not be anything positive, including pi/2.<<br> ==> All DE numerical solvers start @ 0 ... how could it be otherwise ?
>>Ageed.
==> If the period is T , T = � pi describes the sin ... does it ?
==> the numerical solver discretizes both L & T , the solver take only a little part within a reasonable range. It could be the solver options are underdesigned.
==> The other point is that you plot auto, i.e: under error propagation. The same culprit exists in the rk, well illustrated in the Mathcad 8 work sheet [Steven Finch].
>>Where do I find this?
I'm not familiar enough with PDE's to correct or otherwise confirm the way to do..
What I'm saying is that for a unit length L = 1 over T = pi/2 the solver works. If you believe your last "Fourier" plot should decrease exponentially, either the PDE system is incorrect or you have to force the plot to decrease exponentially.
>>Maybe I am just being dense but...solution is (by construction, initial conditions in form of single Fourier mode)periodic in y (with constant amplitude for a fixed time). But amplitude does decrease with t (at least for N > Ncrit). Both top and bottom plots show this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Neither of the analog true solutions functions did show a decay, thus the conclusion the system in incorrect or incomplete. Hope some collab have ideas how to make it work "analog true", then analyse if the solver is insufficient. There is a snake in the garden about the project. Your abstract is superb but does not print much in the mind w/o diagram. Some collab might want to look at other sources.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The failure results from the user incorrect setup.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jwr
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>Thanks. I guess you can't be too careful!
>
>jwr
_______________________
You will never be too careful with DE's, whether analytical or numerical. In my times, DE's resulted from the infinitesimal analysis. The mood has changed. Today, DE's come from the sky under the command of the keyboard ... no more need to look at the existence & uniqueness !!! There may be another route to try, could you scale the system in the numerical range 0...1 ?
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, it makes sense that if the unit L = 1 governs T max = 1.
The analytical solution is not derived. I makes sense as a XFR [Transfer function] of some kind of an integrating and derivative system. A circuit simulation should be possible.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What happened to the pdesolve function till Mathcad 15, where there significant changes - because it claims that variables may not be found?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried schrieb:
What happened to the pdesolve function till Mathcad 15, where there significant changes - because it claims that variables may not be found?
Not sure what your problem is. Both files referenced in this old thread are working pretty well here in Mathcad 15 (M010). See attached pdfs.
Are you using Mathcad 15 with localized language? You may run into a lot of problems if you do (I did using the german flavor of MC) as what is meant to be variable t is interpreted as unit tons, s as seconds, L as litre, etc. Great, when using laplace and invlaplace 😉 You even cannot use lets say t in a quickplot - you would have to (re)define t as a rangevariable beforehand.
Some times ago I used to use variables t. and s. in my sheets to make them look like t and s but it got too annoying and confusing and does not help if you want to use worksheets from somewhere else, e.g. this forum, which use s, t, etc.
It's better to set Math language to english to avoid those problems. But be aware that if you do so, you would have to use the english keywords only. When you open older worksheets the keywords used therein are automatically translated, so you should not run into problems that way.
WE
Edited: Just tried to open one of the sheets while math language was set to german an got the exact error you reported. So I suppose you are using a localized version.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
It's better to set Math language to english to avoid those problems.
...and switch off units:
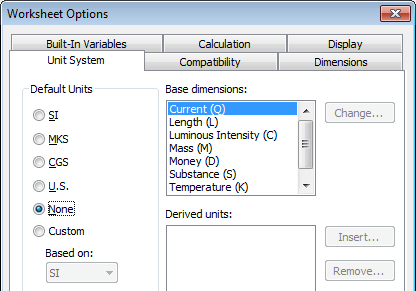
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, thats true. Turning off units helps in this case and many others and you don't even have to restart Mathcad, because its a worksheet option only. But very often that approach is inapplicable, as you may need units in your worksheet, too.
I really don't like Prime but to what I have learned it seems that Prime is doing better in that respect in two ways. First Prime strictly distinguishes between units and variables and second the localization only effects menus and help, but not the math language and I think its better that way.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Yes, thats true. Turning off units helps in this case
1. My Mathcad has this template:
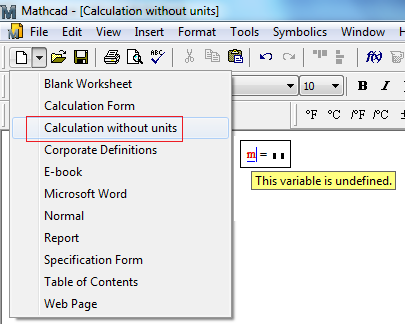
2. Mathcad Prime can work with units by DEs solution but does not have the pdesolve function!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery you are great - switching math language into English helped....
otherwise no single quicksheet using pdesolve works!
shame on PTC
many many thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Efried wrote:
Valery you are great - switching math language into English helped....
otherwise no single quicksheet using pdesolve works!
shame on PTC
many many thanks
You welcome, but...
Sorry - it was Werner with English, I was with units!


