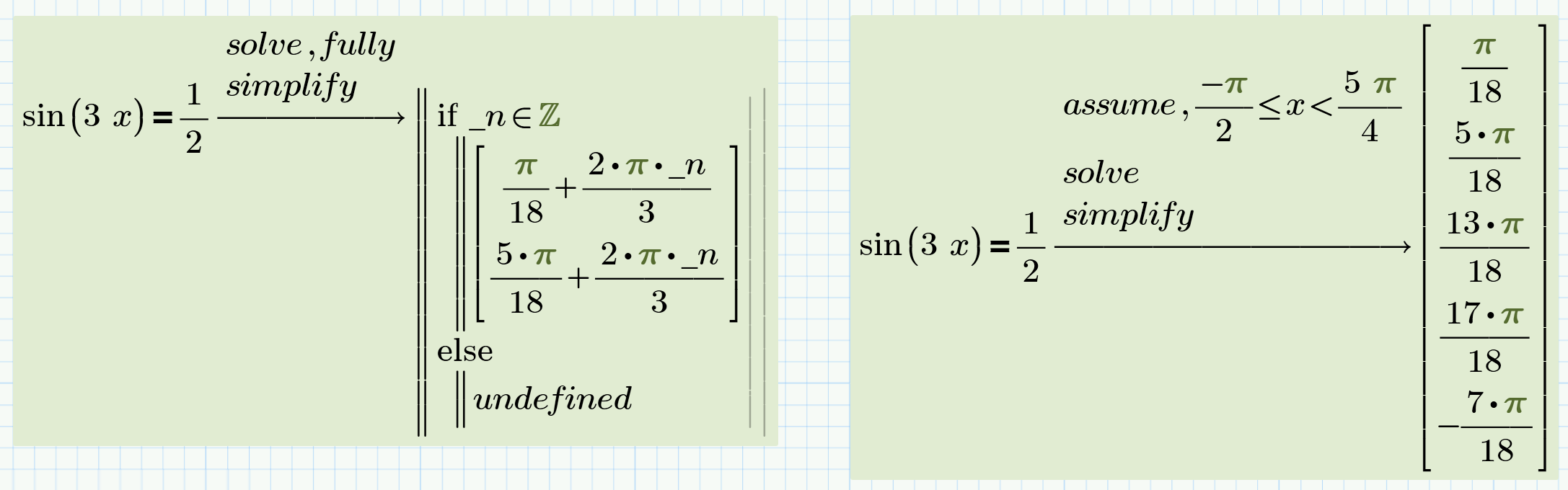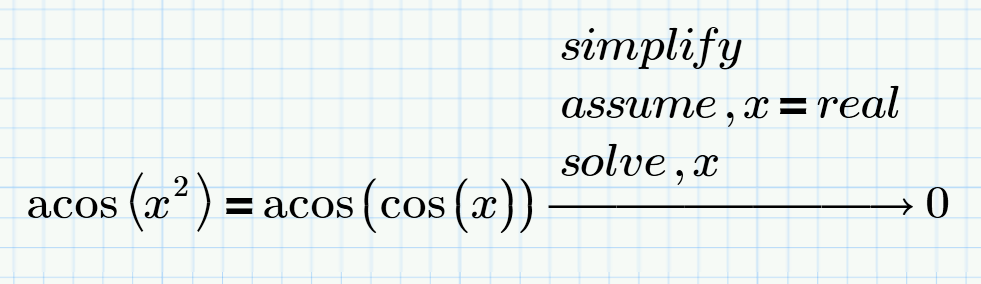PROGRAMMING NEWTON RAPHSON ON PRIME

[XDN]

Hi

I need to use Newton algorythm with prime.

I write algorythm  step by step.

I don't know prime correctly  to make a program for iterative loop.

I need to make 10 loop max, and i want to program break when:

- iterative loop over 10

or

- Error control match with range value Ec

I need to enter manualy first step x0

I need to enter nanualy Error_control Ec

Please, can you help me to write NR with program in prime.

Thanks

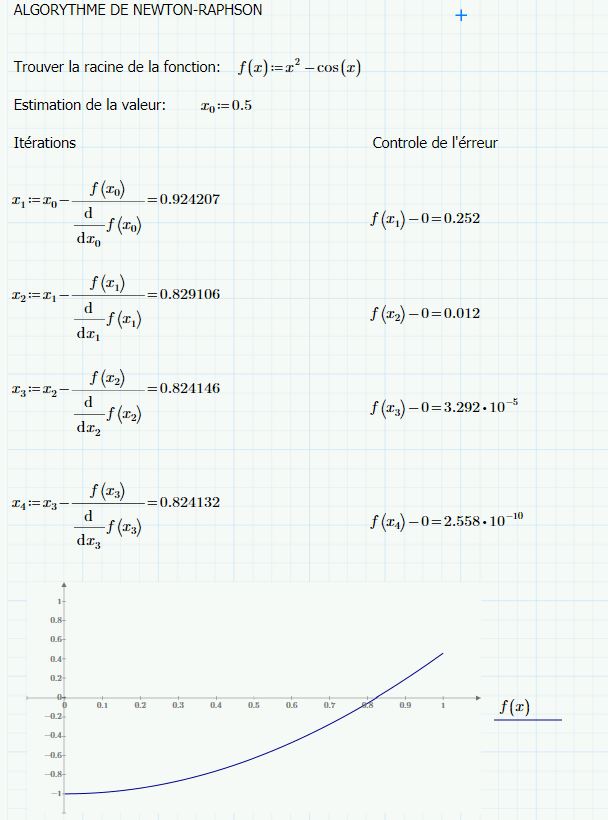
in this capture:

find root for f(x) function with NR algorythm

[Fred_Kohlhepp]

try this

[XDN]

Thanks, it's great!

because i don't understand one things

In you program, where is limited iteration with 10 loop max ?

[XDN]

Another thing

I want the program return only value with range matched

here :0.824146 (the last value of matrix)

[Werner_E]

---

@XDN wrote:

Another thing

I want the program return only value with range matched

here :0.824146 (the last value of matrix)

---

Just read this after sending my reply.

To get what you want in Freds sheet you would just change the last line to "return ans[i" (that is ans with vector index i).

To do it in my version, you would change the last line to "return x[i".

BTW, Fred did not implement the limit of maximal 10 iterations, in my version the max number of iterations is an argument of the Newton-function.

If you just need the result, why don't you let Prime look for the solution (look in my sheet after "Check:" for a few ways to do it.

[Werner_E · Accepted solution]

Here's a slightly different function with two additional arguments - function and max.iterations - and a table as output:

Worksheet in P4 format attached.

[XDN]

It's ok for me !!!

Thanks!!!!

For my use, it's not necessary to iterative loop is "var"

ten value will be implemented in hard.

But it's more pretty in your solution

[ttokoro]

Dear Werner

Your sheet is very useful and give us many hints how to use Prime 4.0.

I have a small question.

In your sheet

f(x) is solved 0.824... , however, above shows -.0824...

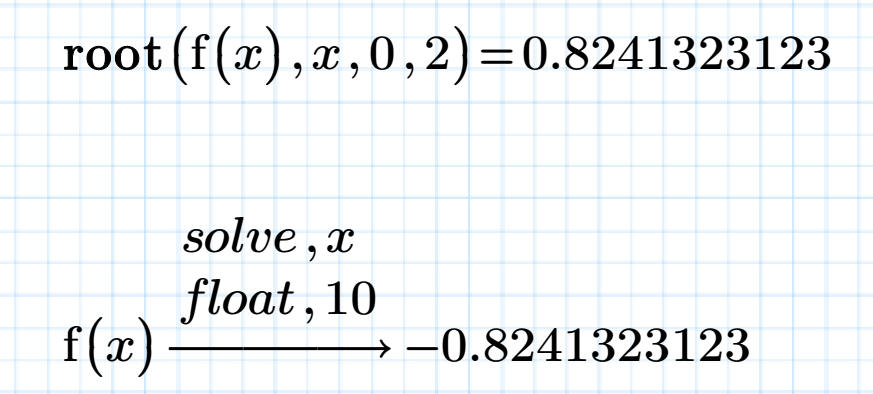
Is their any way to solve it by + value?  (Not -0.824 but 0.824)

Tokoro 

[Fred_Kohlhepp]

---

@ttokoro wrote:

Dear Werner

Your sheet is very useful and give us many hints how to use Prime 4.0.

I have a small question.

In your sheet

f(x) is solved 0.824... , however, above shows -.0824...

Is their any solve it by + value?  (Not -0.824 but 0.824)

Tokoro 

---

If you look up the root function in help you will find out that the "0,2" (the last two arguments in the function call) specify the range of values to search for roots in.  This is useful when there are multiple roots and you need to force a range.

[ttokoro]

Thanks to reply my question. I try to get the positive amswer as above, houever, Prime say "No answer".

I want to get positive answer by symboric operation.

Tokoro. 

[Fred_Kohlhepp]

"root" is not a symbolic function.

Mathcad is primarily a computational engine, with a very weak symbolic engine.  If you are going to want mostly symbolic solutions you should investigate other resources.

[Werner_E]

---

@ttokoro wrote:

Dear Werner

Your sheet is very useful and give us many hints how to use Prime 4.0.

I have a small question.

In your sheet

f(x) is solved 0.824... , however, above shows -.0824...

Is their any way to solve it by + value?  (Not -0.824 but 0.824)

Tokoro 

---

I must confess that I didn't even noticed that the symbolic solve did not return the same value as the numeric methods.

I can only second what Fred so often writes. If you need a numeric value you should use numeric methods like the root function or a solve block. Thats what Mathcad was made for initially. The symbolic engine (which now is an old an limited version of muPad) is by far not as capable as programs like Maple or Mathematica.

Use the symbolics if you are working with unknown variables and need a symbolic solution or if you need all solutions of an equation or all solutions within a given range like in the examples below:

But if the equations get more complicated its more likely that the symbolics can't find a symbolic solution. In that case (and if all other variables are defined) it will switch to some kind of numeric mode (still more precise as the numerics in Mathcad, but numerics). I don't know anything about the algorithms the symbolics will use when switching to numerics mode, but they sure must have implemented some way to determine a guess value. And this may be the reason why, when the symbolics switch to numeric mode, "assume" commands seem to be ignored.

Normally the answer to your question about how to get the positive solution would be "simply add: 'assume,x>0' !". But as you probably have already tried this results in a silly "no solution found" error. In other cases that kind of assume statement may simply be ignored and the returned solution still would be negative.

So as sadly as it may be, the answer to your question is "I can't think of a way to get the positive solution reliably using the symbolic solve command".

Sometimes you may have luck by rearranging the equation or perform some kind of manual transformation of it - but thats just a matter of trial and error and luck:

And sometimes we even get simply WRONG results and thats really very bad in my opinion!

Not being capable to solve an equation symbolically - sad, but OK for a number cruncher.

But returning a wrong result, thats an absolute no-go!