Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Parabola-Mirror - an error?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Parabola-Mirror - an error?
Where is an error? Help please!
(One more same problem What is not correct in this optic problem?)
I know other simple solution this optic task (see please bellow), but I would like use this:

Simple solution - symbolic (by WolframAlpha.com site) and numeric (with nanotechnology help![]() 😞
😞
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
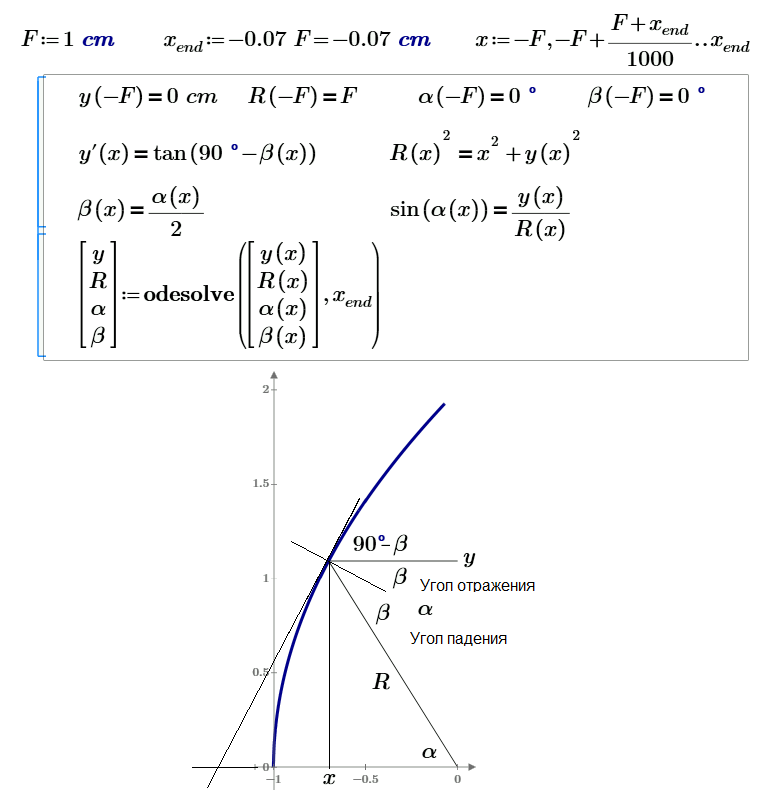
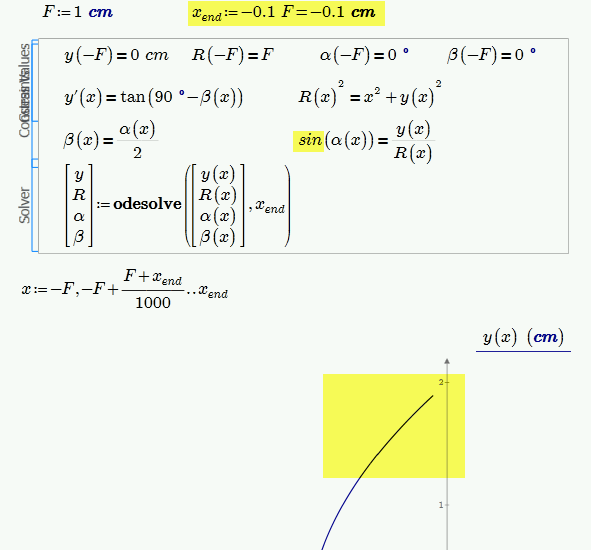
Seems to work for negative values of x only.
Not sure and I had not tried (Prime is crashing all the time with your sheet) but maybe you run into the same problems with tan as I did in my solution above (y' gets infinte when x=0)
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What do you mean by this equation

and where does it stem from?
And why do you think that the argument of y´ should be a length (x(alpha)) while the argument of y is an angle?
If you write y´ here it has in any case to be the derivative with respect to alpha.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, Werner - not alpha but x - see please bellow
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may be able to keep alpha as the independend variable, but you can't use y'(x(apha)).
What you mean is

which Mathcad can't unserstand and you will have to replace it by

If you do so, other errors occur, though.
But I see you already rewrote your equations to accommodate for x as the independent variable, anyway.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, but

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I told you that you will run into other errors so it seems it was only the first mistrake in a row of others.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From unnecessary ballast freed system but I don't understand what the error message would like to tell us!?
Looks like Mathcad does not like both derivaties to be in one equation.
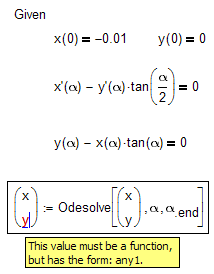
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here we go.
It was necessary to introduce a dummy function and to redefine tan(). Not convincing, but at least it works.

Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you need to do it like the following Valery:
Note that the gradient is infinite at x = -F, which leads to difficulties for the integration routine. Hence the definition of the gradient function above.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alan and Werner.

The Prime 3 sheet in attach is without an error but has a false tan not sin in the last equation.
I feel the error but...

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Seems to work for negative values of x only.
Not sure and I had not tried (Prime is crashing all the time with your sheet) but maybe you run into the same problems with tan as I did in my solution above (y' gets infinte when x=0)

WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you know a surface with this Law of reflection:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why are you trying this the hard way?
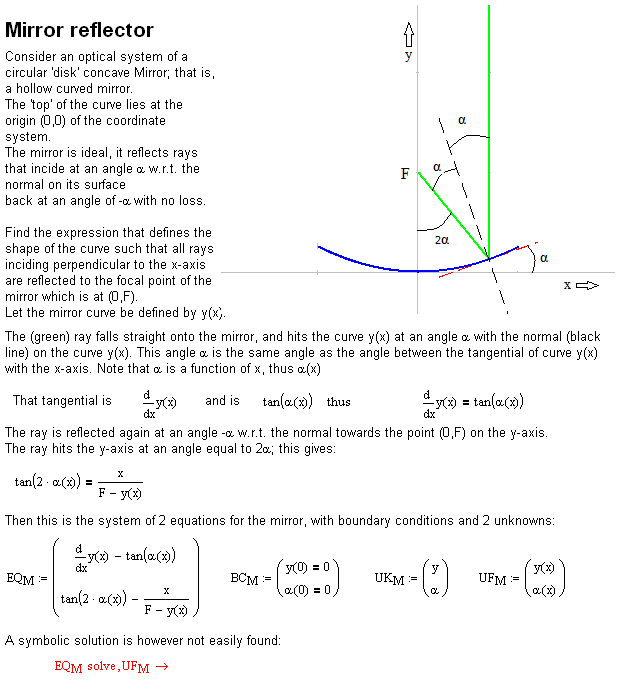
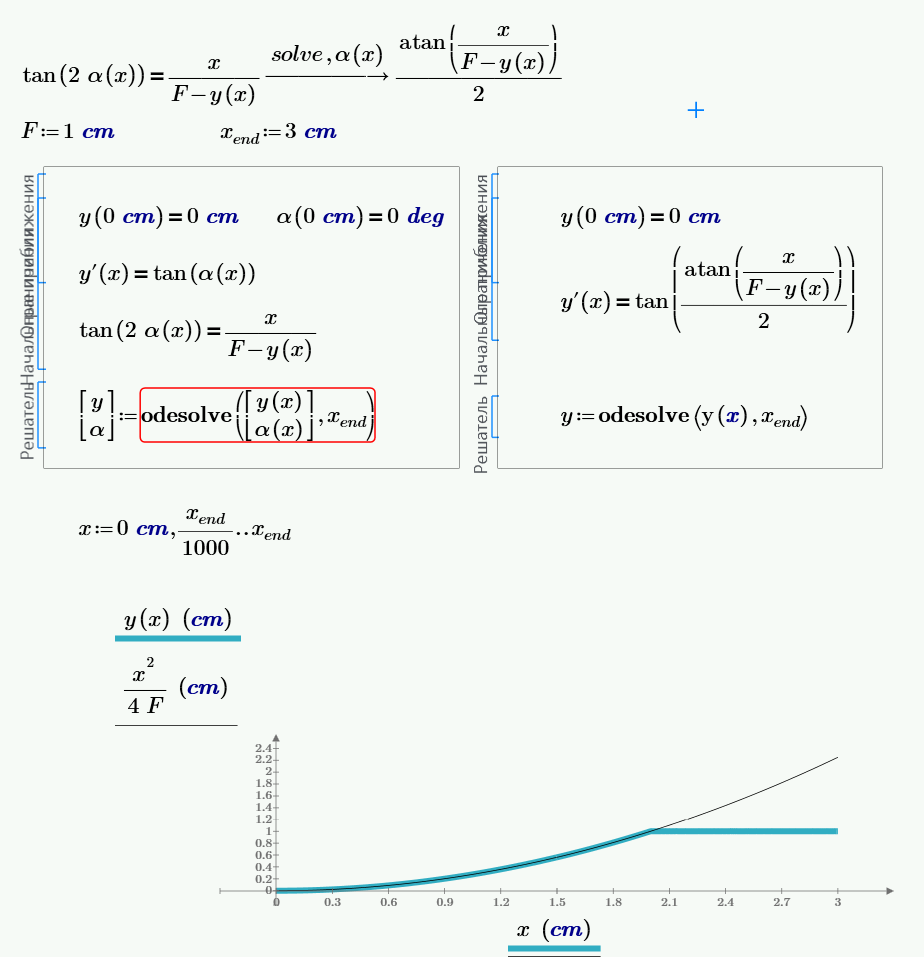
Numerically it is possible to solve this, but it can also be done symbolically:

Here is an animation
Note that the solution also works when F is negative, then the mirror is convex instead of concave.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Those embedded videos don't work (as so often).
Better simply attach the original avi-file.
-> Better qualitiy, more convenient to watch and more reliable
Here is what I see:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Those embedded videos don't work (as so often).
We must load not avi but mov files. I do so and no problem!
And it is good to attach avi and mov files to the messege.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It should work with avi's, too. Having to convert animations to another format is an annoying additional step of operation.
But then, I never liked the embedded videos here in this forum for various reasons. Since the last forum design change it seems to have become worse.
Anyway, I played around with your last version and stumbled upon a quite strange effect.
**** DELETED *******
The real reason for the peculiar effect was sitting about 40 cm in front of the screen 😉
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, here is really a strange effect.
Why does this small change of the end value has such a big impact on the overall shape of the solution??
I could understand if the algorithm goes havoc near x=0, but not at the start at x=-F.
Or is it working from x.end back to the start? Don't think so as it has to use the initial conditions for x=-F first, I guess.

Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A lens not mirror - but two video - from avi and mov files
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
Your animation is not visible for the viewing. Please attach to the message the archive of this animation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
VladimirN. написал(а):
Luc,
Your animation is not visible for the viewing. Please attach to the message the archive of this animation.
See please:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I noticed it wasn't visible. I even got to see my animation attachment efforts as separate items in the topics list:

but with NO access allowed. When I try to select one, Iget:

Here's a zip file with the AVi's.
Enjoy!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Luc, did you do this analysis in Mathcad 11 or Mathcad 15? If in MC11 would this work in 15 seen the different symbolic engine? Happy New Year and thanks for the many very instructive worksheets over the last years.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
Numerically it is possible to solve this, but it can also be done symbolically:
Symbolically it is possible to solve this, but it can also be done numerically:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
Why are you trying this the hard way?
I would like to solve this problem!
Do you know material of this mirror surface?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How can we use the try (on error - Mathcad 15) operator: