Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Pulse function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Pulse function
I need a "forcing function" that will be continuous (not piece wise). It needs to be a rectangular function with amplitude "A", Period "P", and duty cycle "D" (40%) that is a function of y(t) for some time period "t".
Can anyone help me out with this?
Thanks,
Mike
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
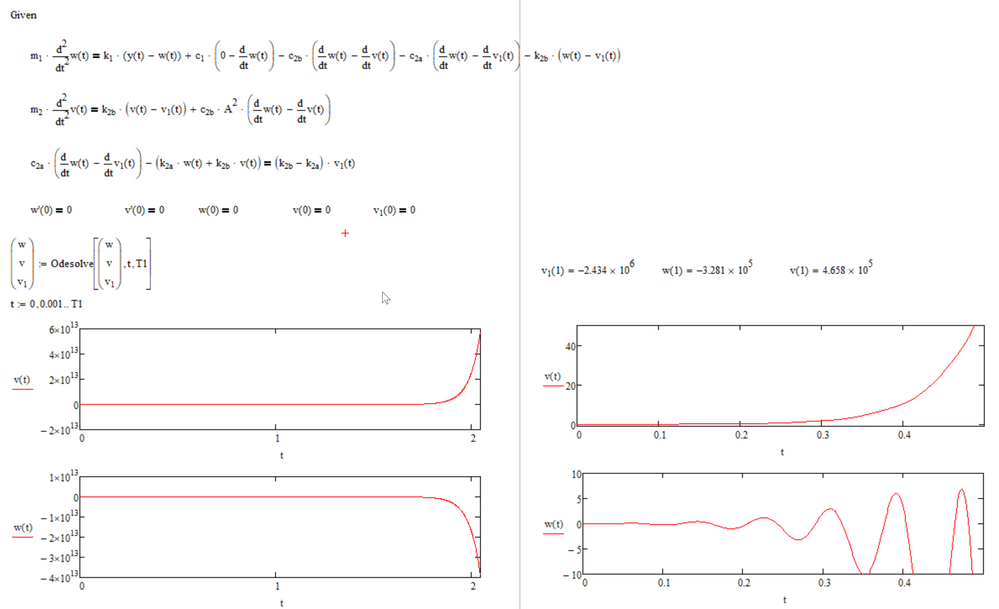
I am stumped with the attached sheet. It tells me I have too many initial conditions. If I delete one then it tells me I have too few. I have the feeling that is not the real issue, but I do not know what is. I don't feel like the help files are much help on odesolve. Can someone help out on this one?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You sure messed up badly with the parenthesis - check them in the first and third equation!! The outer one in the third equation is unnecessary and they sure are quite wrong (and a closing one missing) in the first one.
After you correct this you have to add a fifth initial condition, something like v1(0)=???
Furthermore you have to switch the sides in your third equation as Mathcad prefers the derivatives at the LHS.
To speed up the calculation you should pre-calculate the first derivative of y(t), otherwise its calculated from anew for every iteration step. You may let the symbolic do the job by writing y1(t):=d/dt y(t) -> (symbolic evaluation) or you do the derivation yourself and define y1(t):= as the appropriate sum. Then use y1(t) instead of d/dt y(t).
But in your case y(t) should be a rectangular signal, so the derivation is zero anyway! (Apart from some single Dirac's. So you may replace d/dty(t) by zero.
Is there any reason why you are using that time consuming and inexact Fourier series instead of the pulse function which Luc provided? In your first post you showed a function where the duty cycle starts at t=0 and now you use another one where it starts at t=0.025. It would be easy to change Lucs function to do the same!
I did some changes (see picture below) but the first equation sure should read differently as with the function I came up with we get very high values at the end of the interval (10^13) which probably is not as expected.
BTW, your range definitions for t still are wrong!!
The first one (note the red dots) because the dots (..) are interpreted as unknown variable and the second one because you still use the unit s.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
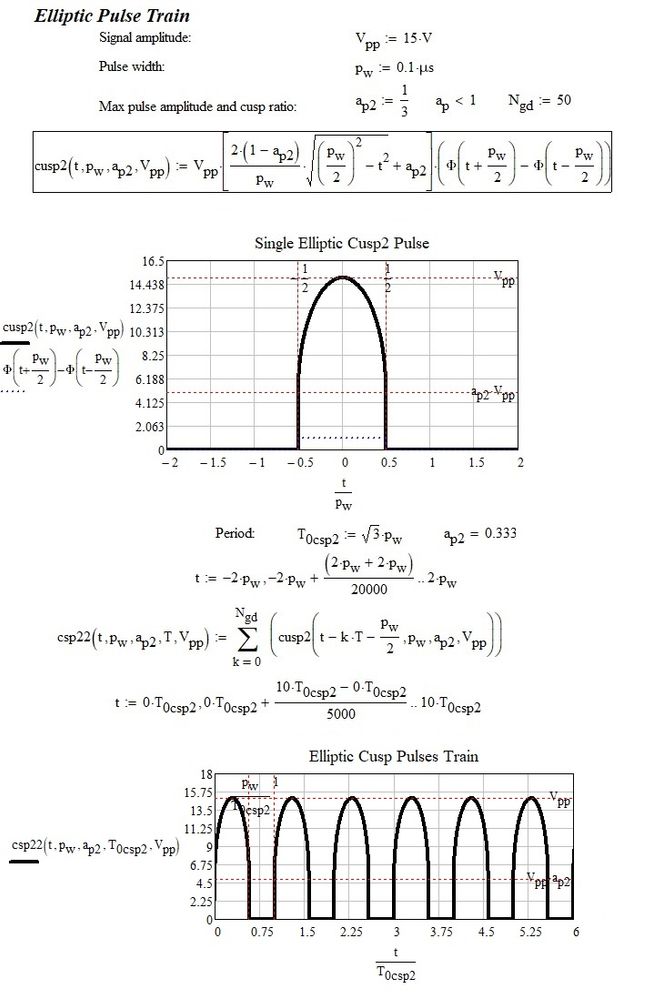
Thank you for this interesting idea. However, I need it to be rectangular (as proposed by Luc), not elliptical.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
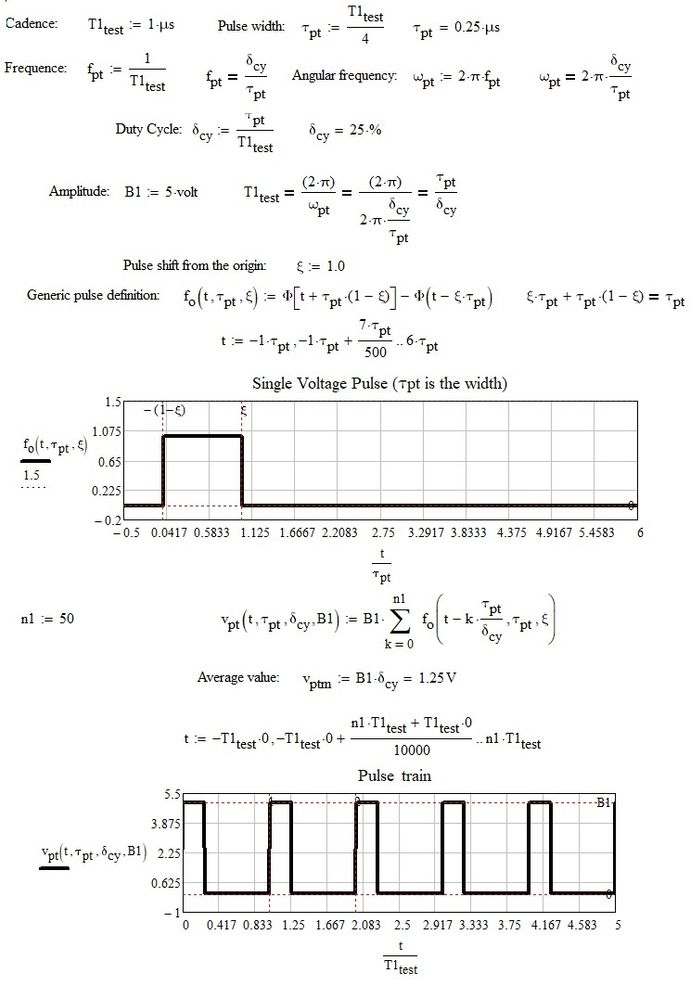
Ok!
that's better?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That is definitely better. Now my next question - how do I turn that into an equation of the form y(t)?
I have a lot of other equations on down the Mathcad program that are using y(t) in their evaluation. This program is using this pulse as a "description" of a road surface that is then being used to evaluate the suspension on a vehicle that is driving over it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
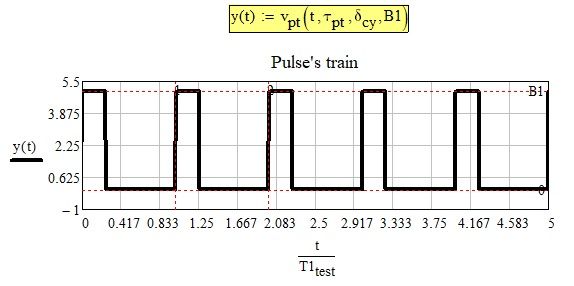
it is very simple:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Could you possibly send me this as a Mathcad file? I must be entering something incorrectly. It is not working for me.
Thanks very much,
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- « Previous
-
- 1
- 2
- Next »