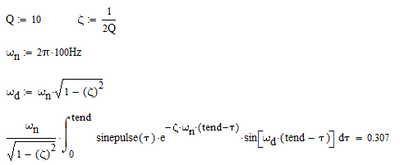Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Return max value from a Convolution calc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Return max value from a Convolution calc
I have to revisit some "old" mcad 15 as I lost some of them.
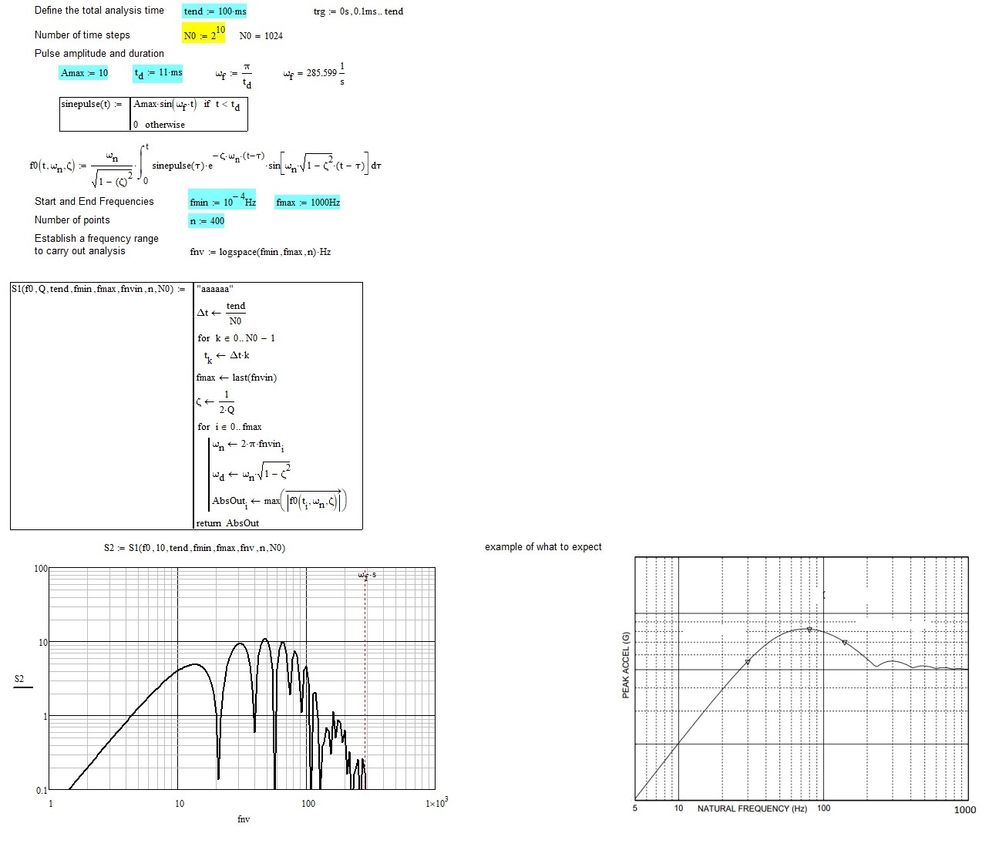
I am setting up a Convolution calculation for a given input (half sine) to extract the max response for a given range of frequencies. However what I am getting out does not appear to be correct.
Can anyone wit the expertise have a look and point me toward what is wrong?
- Labels:
-
Programming
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The expression inside the "max" function in your program yields just one single scalar value (not a vector) - so what do you expect that "max" should do?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I thought the expression would return a "graph" as if I take the expression between the max() and plot it I get the attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't see how the function QQ and the variable tr in your picture are defined and how this picture would relate to the sheet you posted and your question ??
In your sheet you try to take the maximum of a single scalar value.
For every of your 400 frequencies (in the example below I had chosen 100 Hz) the expression in your max function (basically a definite integral) would yield just one single scalar value.
max would normally work on a vector of values but if you simply provide a single scalar, max would return juts that value.
Here is what you calculate 400 times and this is what you final plot would consist of:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
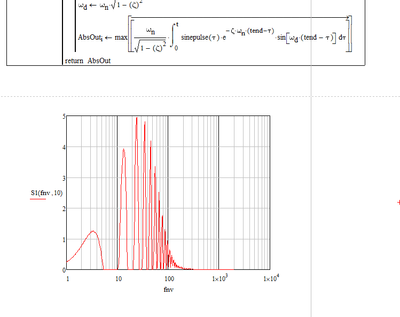
Was just playing with something - see attached
I am confusing the integration limit I think as I really want to pick up the max value
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In your program the upper integral limit is constant t.end.
If you change it to variable "t" (which is defines outside of the program in front) is makes sense to use "max". Of course you would have to vectorize the expression.
It took a long time to calculate (vector t has 4096 elements) as the integral had to be calculated 1638400 times.
The result is still not what you expect.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. I don't really get it so will have to do some digging
Indeed can take a long time to do the integral calc. I reduced the number of frequencies for the test
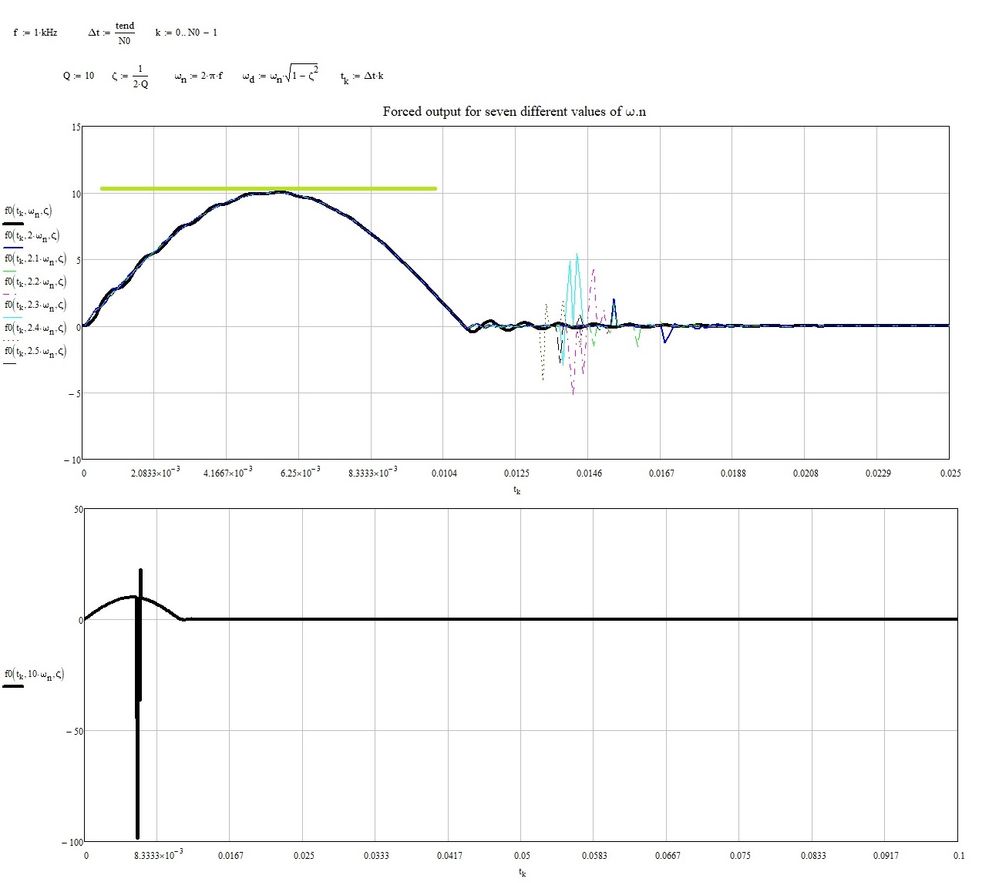
I had a go, see attached, with 2 frequencies and it seems that I can get the max value I am after no problem. I can also plot the "integral" over time ie the response and again looks OK
I do not really know why I cannot loop over a range of frequencies
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I notice that in your program you have two times the expression (tend - tau) but in your function QQ it reads (t-tau).
Furthermore it looks like Mathcad has problems with the vectorization of the integral. Putting the integral in an auxiliary function helps:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks a lot for pointing the error - A oversight from my part
You proposed correction seems to move the problem in the right direction. Thanks a lot
Will look further into it later tonight or tomorrow as clearly there is a problem at higher frequencies
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
It is not necessary to perform convolution in the loop:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
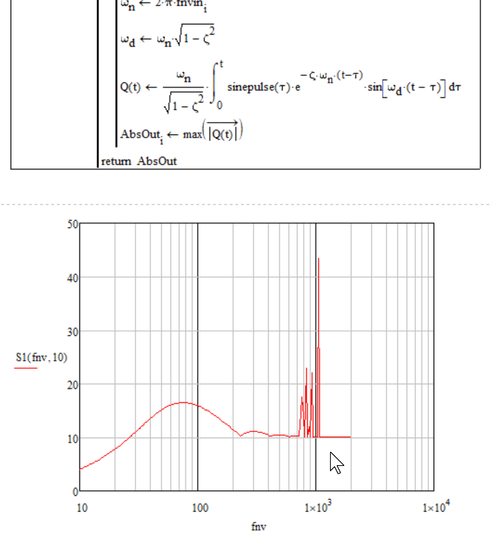
Apologises for the delay in replying - Was busy looking at others "methods" (python script, etc)
The method proposed is a lot faster but does not give a correct answer. At high frequency the plot should stabilise around the Amax value (10 in this case or 1 it scale the data by Amax). I attached a comparison plot which shows that my 1st pass coding of the convolution seems correct with some issues in some frequency (spike). I compared my prediction against 2 other methods (Method #2 is a 1/3 party tool (a black box)).
I think the issue with your propose method is the use of t[i in the function f0()
Can one of the math expert (@LucMeekes springs to mind) put some light on why one get spikes in my plot?
Thanks in advance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
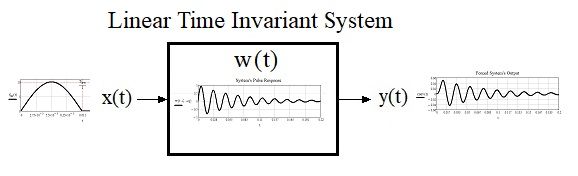
It is clear that the system in question is a linear and stationary system of an unknown nature. The analytical relationship between the response and the excitement of a linear and stationary system, whose impulsive response is known, is given by the convolution between the two and constitutes the forced response of the system. See image. What leaves me a little perplexed is that you ask the simultaneous trend of the maximum value of the response to the variation of time and frequency (it can be seen from the loop with index i) which does not seem correct to me. Since the system is linear and stationary, the Laplace transform is commonly used, and thanks to the Borel theorem, from this, with an inverse Laplace transform calculation, one gets the forced response as a function of time. For the analysis in the frequency domain, just put, then, s = jω into the transfer function and plot the Bode diagrams. Knowing the forced response of the system, It is possible to determine the peak of the forced response and then to determine its trend as the frequency changes.
This, however, requires many laborious and difficult calculations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the explanation.
The system is a simple 1DoF Spring-mass of natural frequency fn (or wn). This system will response to an input (half-sine input) and I am calculating the shock response spectrum SRS. For each natural frequency in a given range, calculate the time response (using convolution) and extract the max response that's the time part. One end up with a pair of data (fn,max acceleration). To qupte from your response. ".. It is possible to determine the peak of the forced response and then to determine its trend as the frequency changes". This is what I am doing
Still haven;t figure out why I get spikes in the response
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Knowing the forced response, then the graphs of the same can be traced for different values of the pulsation. The graph shows that the maximum amplitude is constant with the variation of omega. As you can see, the graph in logarithmic scale, varies with the variation of N0, while the answer is unchanged.