Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Seven math curves
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Or use more than one focal point. What about a curve, where the sum of the distances from three points is constant.
Regards
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice find!
I vaguely remember having heard (a long time ago) from a Tschirnhaus-curve (but not sure - I may mix up things and be wrong about this).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Why be content with seven when you can have eleven or more ?
Regards
WE
We have 7 operators in Mathcad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
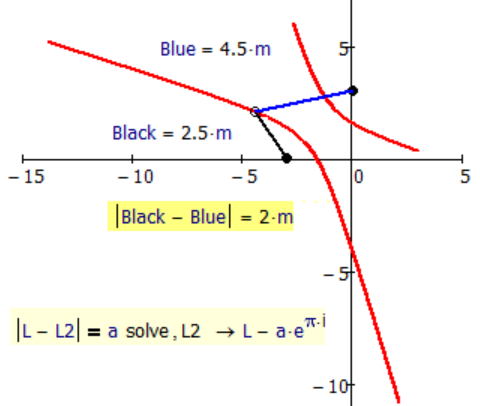
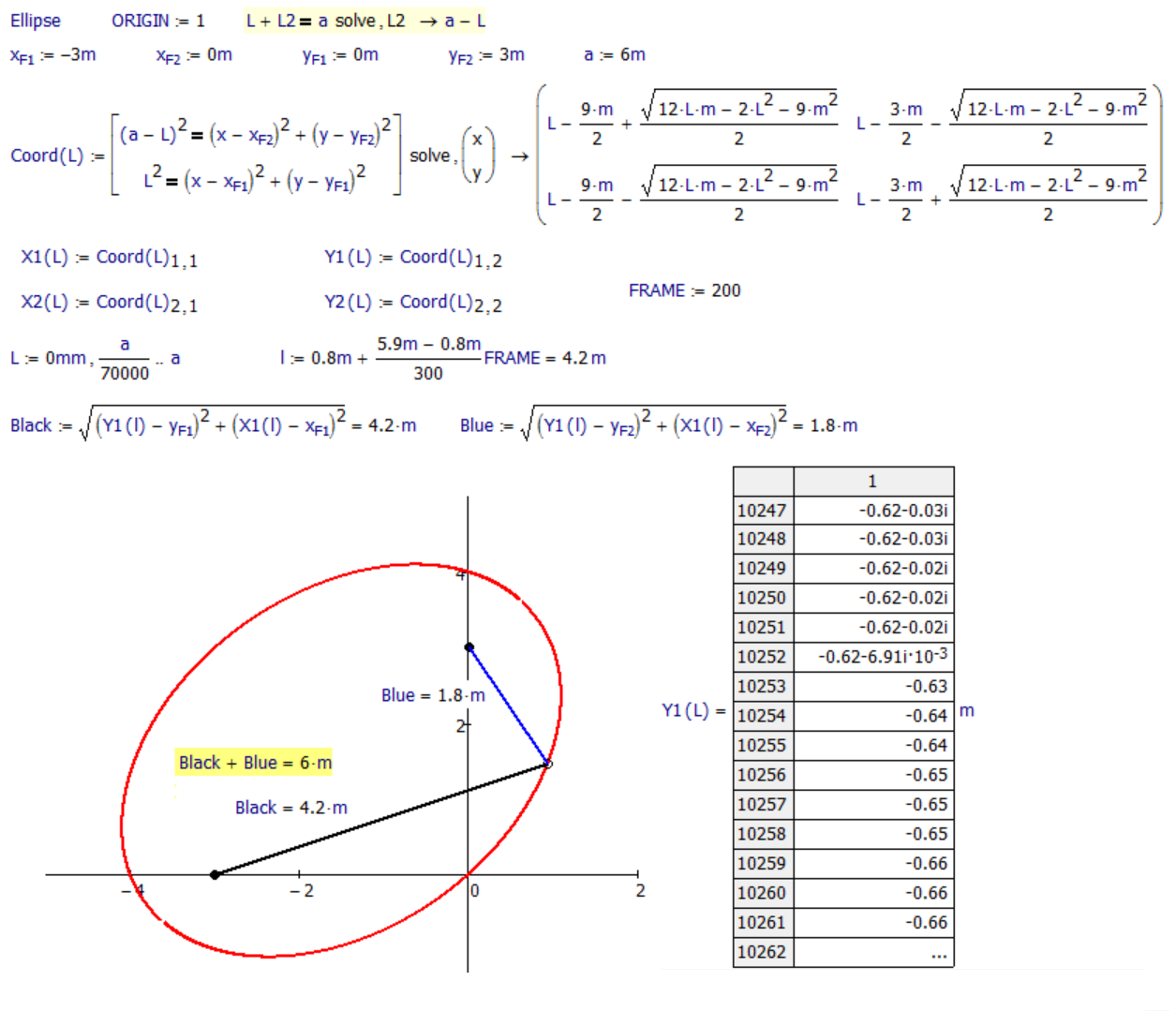
1. black+blue
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice worksheets.
I see that you, too, determine the limits of the radius L by hand (trial and error, I guess).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
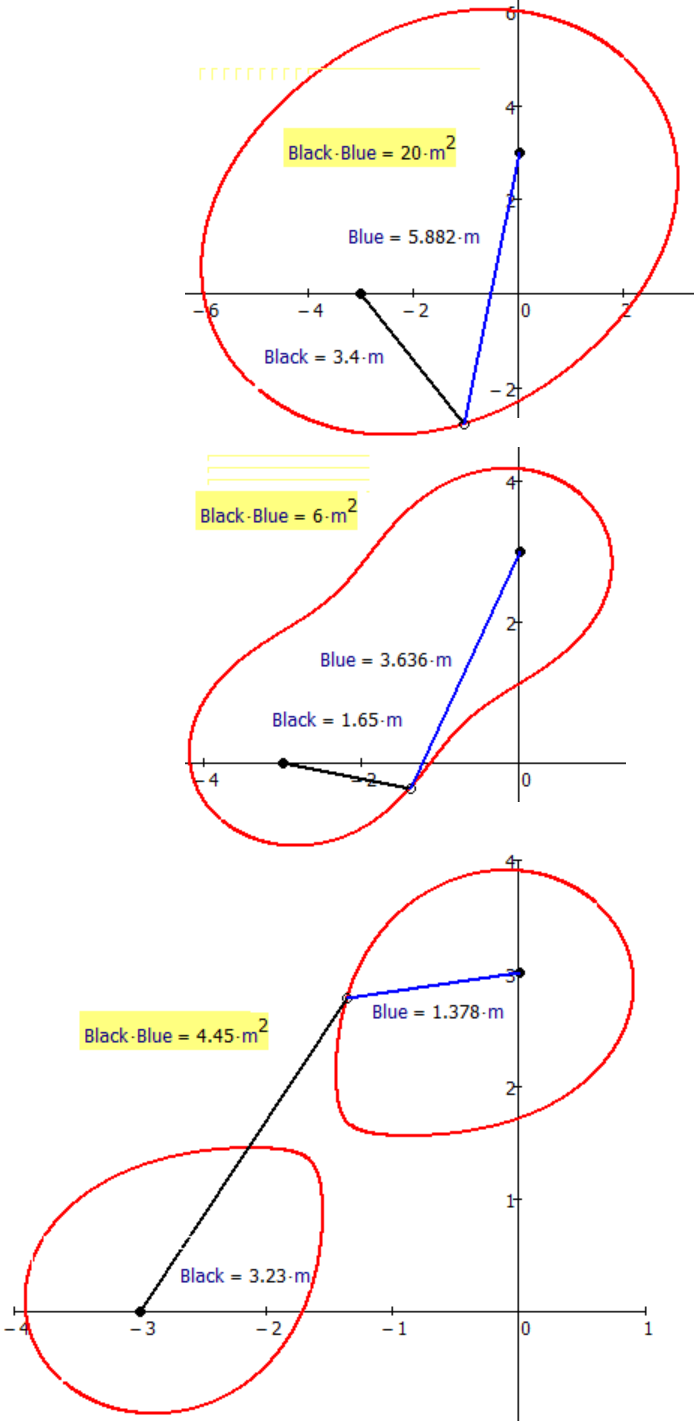
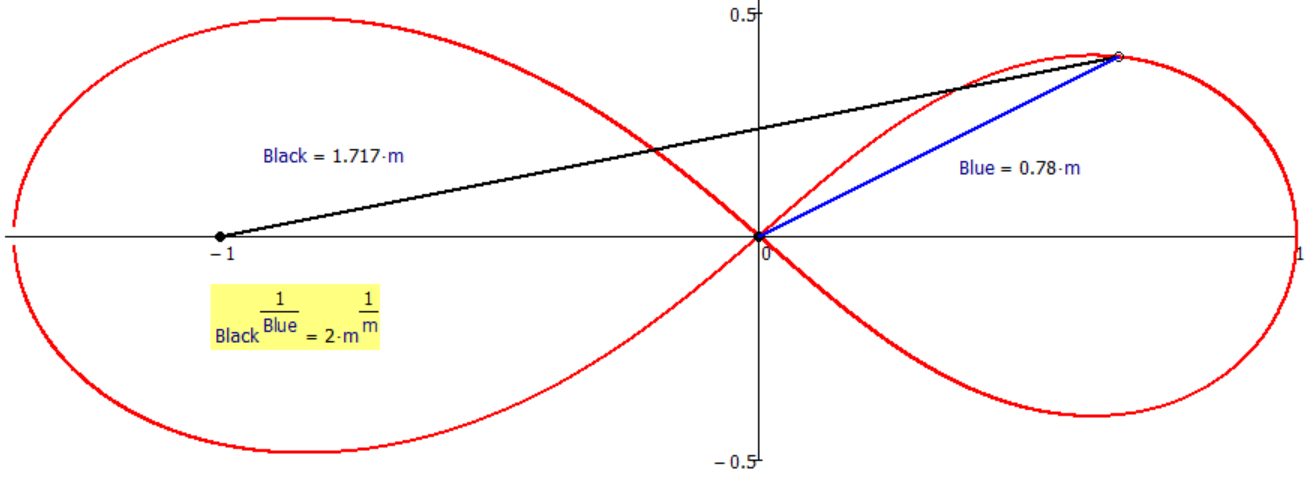
7. blue-root of black - with new focuses and with two branches
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
With two branches: one log(Black, Blue) and others log(Blue, Black):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
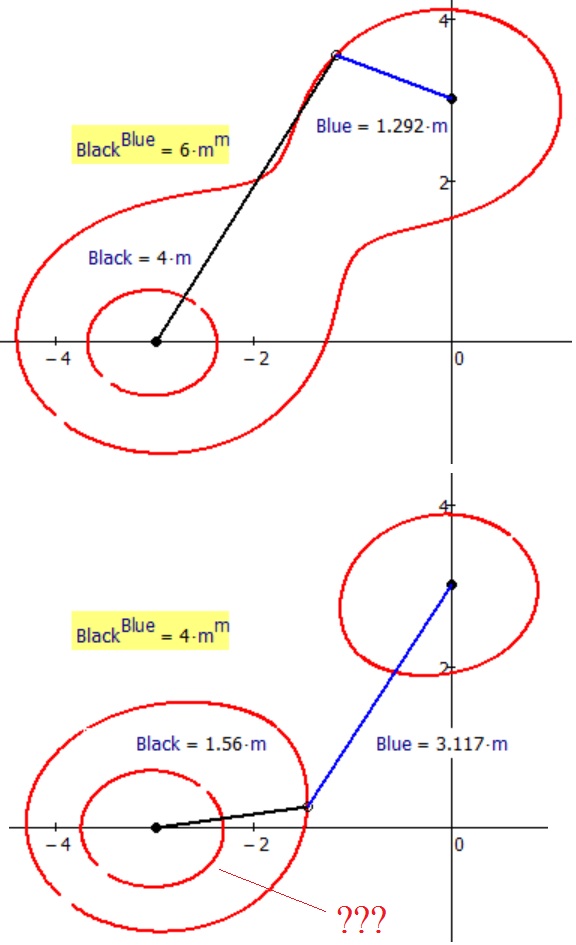
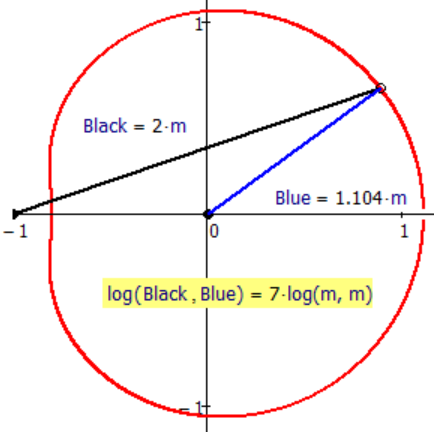
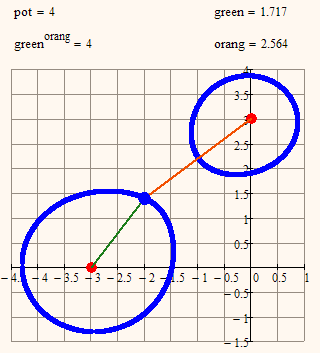
> 5. black^blue=const
Nice, but the unit "m^m" is still wrong 😉
What about the "???"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
> 5. black^blue=const
Nice, but the unit "m^m" is still wrong 😉
What about the "???"
Why wrong?
I'm going to do at my dacha for a bed of flowers in the form of this oval with a physical characteristic constant 7 (m^m), not 6 (ft^m) or 5 (m^ft)!
> ??? - I do not know what is this little close curve ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Why wrong?
We had that discussion already in the other thread, so I won't repeat it here. Just one thought: (2m)^(3m) = 2^(3m) * m^(3m) = 8^m * (m^3)^m. So its NOT 8 m^m . Now do the same game with different numbers!
> I'm going to do at my dacha for a bed of flowers in the form of this oval
Why not, if a simple ellipse is not challenging enough 😉
> with a physical characteristic
Sorry, but its no physical characteristics and its a characteristic dealing with the numbers only, not the units. But it sure is a nice leisure activity anyway.
> > ??? - I do not know what is this little close curve
Obviously, if you did not make a mistake, its part of the solution curve. Just give it a try and see, if black^blue still is 4.
EDIT: There is a mistake: If L<1, then L2 would be negative and no solution exists!! But your "Coord" yields solution because L2 (as radius) is squared in the circle equation. You have to take care of this and simply let L run from1 upwards (L=1 would provoke a divison by zero, of course which could be dealt with an on error statement).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
> Why wrong?
We had that discussion already in the other thread, so I won't repeat it here. Just one thought: (2m)^(3m) = 2^(3m) * m^(3m) = 8^m * (m^3)^m. So its NOT 8 m^m . Now do the same game with different numbers!
> I'm going to do at my dacha for a bed of flowers in the form of this oval
Why not, if a simple ellipse is not challenging enough 😉
> with a physical characteristic
Sorry, but its no physical characteristics and its a characteristic dealing with the numbers only, not the units. But it sure is a nice leisure activity anyway.
My friend in USA would like to create same bed of flowers (клумб с цветами) in his garten. He has a rule not with meter and cm but with feet and inch. I send to him the coordinate of 2 points (focuses) with feet and inch and the constant a with.... What numeric value and UNIT must I send in America? Or I must send the rule with meter and cm scale?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Better send him the ruler in metric units as your flowerbed does not scale (the property a^b=const. does not scale). And don't forget to tell him that he should only use the numbers taken w/o units when he calculates the powers 😉
You haven't answered (2m)^(3m)=? and now (6,562 ft)^( 9,843 ft)=?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
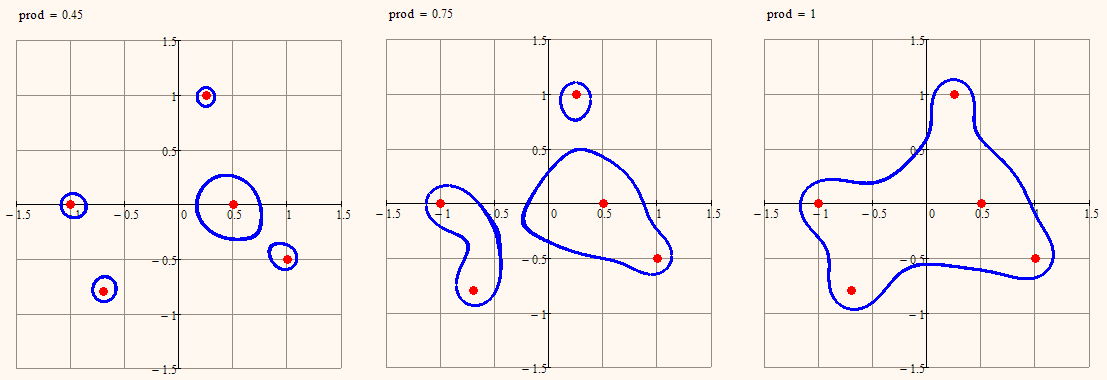
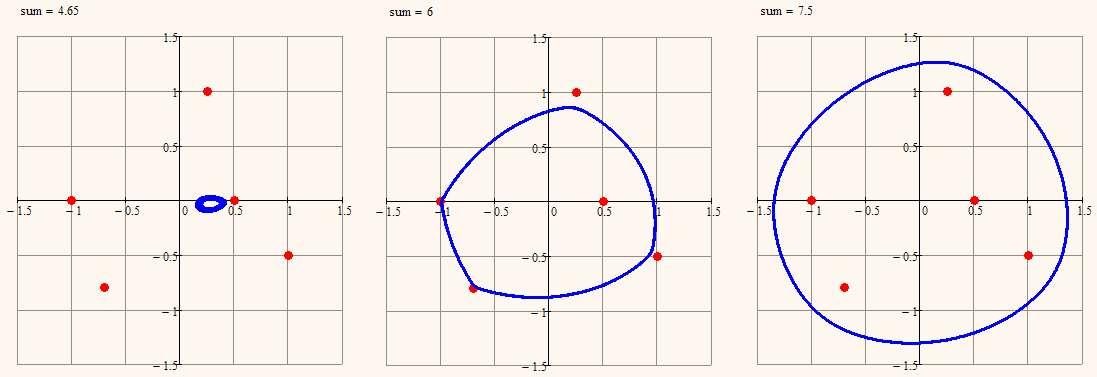
Here are some curves which should scale. Simply stay with basic commutative operations + and * and simply use more points:
Here the points whose sum of distance from five points is constant:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Here are some curves which should scale. Simply stay with basic commutative operations + and * and simply use more points:
Here the points whose sum of distance from five points is constant:
Animation:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And here is the same with constant product of distances
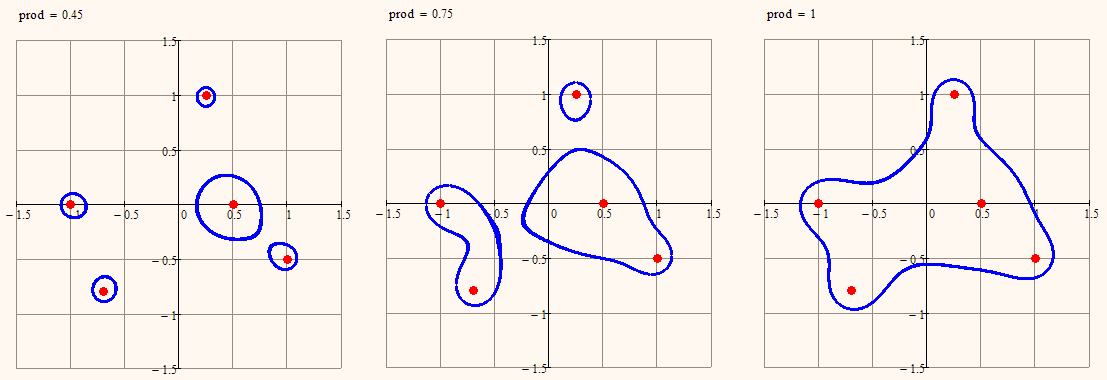
Guess I have finished playing around with those curves. Can't think of a way to derive a closed parametric equation for those beasts.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please do one more with 7 points - 7 is one fine number!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
And here is the same with constant product of distances
Animation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
And here is the same with constant product of distances
Guess I have finished playing around with those curves. Can't think of a way to derive a closed parametric equation for those beasts.
It is a lemniscate with 5 focuses - see please Лемниската — Википедия
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The discription is not available in the English or German version of Wikipedia.
I am not sure if all those curves should be called lemniscates.
In the two focal point case we speak of Cassini ovals and only if the constant product is the square of half of the distance of the two focals, we speak of a (Bernoulli) lemniscate. So the two focal lemniscate is just a special case of the Cassini curves.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
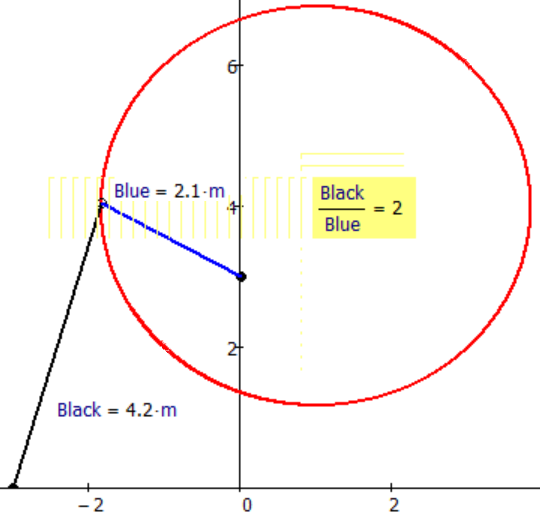
Bicycle Apollinaire - two branches: Black/Blue and Blue/Black: