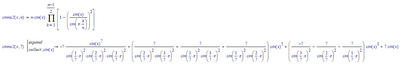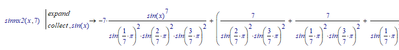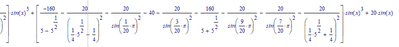Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Sinus Polynom
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sinus Polynom
Hello,
In 1594, Adriaan van Roomen set the task of determining the zeros of a polynomial of degree 45. This was quickly resolved by Vieta by taking a close look. One quickly discovers that the sine of 45*x is to be expanded by a polynomial in sine(x). I tried to understand this in the attached file. Mathcad 14 went on strike. I am asking for hints how to expand the product in attached file for n=45 into a polynomial. Mathcad drops out at n=11.
Kind regards, Alfred Flasshaar
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Actually Mathcads symbolics does not fail but simply refuses to display the result because it considers the expression with the 32 summands which you get for n=11 as being too large for display. You assign the result to a function of x and use it in further calculations, but unfortunately thats not what you want (you yculd use sinn(x) right away) - your goal is the display of the sum only.
In Mathcad 11 a registry entry could be set to let it display larger results as well, but to the best of my knowledge there is no way to do something similar in MC14.
You could use some shortcuts and substitute in your mind. That way you can get Mathcad display the expression at least for n=11 as well but for n=13 this again is to large to display ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Actually Mathcads symbolics does not fail but simply refuses to display the result because it considers the expression with the 32 summands which you get for n=11 as being too large for display. You assign the result to a function of x and use it in further calculations, but unfortunately thats not what you want (you yculd use sinn(x) right away) - your goal is the display of the sum only.
In Mathcad 11 a registry entry could be set to let it display larger results as well, but to the best of my knowledge there is no way to do something similar in MC14.
You could use some shortcuts and substitute in your mind. That way you can get Mathcad display the expression at least for n=11 as well but for n=13 this again is to large to display ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Like this:
For n=20 Mathcad 11 gives me an expression that starts with:
and ends with
(Note that there's a huge middle part)
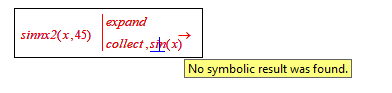
For n=30 the calculation took longer than I was willing to wait.
But for n=45:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many Thanks. Strictly speaking, I'm interested in the integer coefficients in the cumulative expansion. It is Mr. F. Vieta's admirable way of thinking that arouses so much curiosity.