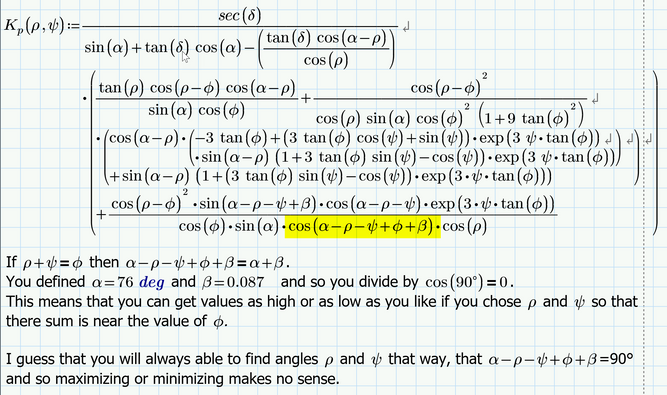Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve Block maximum value solution with multiple dependent variables
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve Block maximum value solution with multiple dependent variables
I would like to solve a non-linear equation for the maximum value. The equation has 2 dependent variables and the solution represents the maximum value for a given number of independent variables. (see equations below).
The dependent variables are initialized at the start of the solution and the largest values of Ka and Kp are calculated for the independent variables.
I will try the solve block solution with 2 guess variables and see how the results compare to the published solutions. I would appreciate comments/suggestions if there are other methods of solving the equations.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Based on the published solution, the maximum value of the function for the given inputs should be in the range of 2.56 - 15.73
And you got a value of approx. 2000. That means that "maximize" did a good job, doesn't it?
Which version of Prime the file was created in? After recalculation in Prime 9 I get an error message because maximize was used the wrong way. K.p is a constant (6.02) and you used it as a function. Actually I wonder why this worked in any version of Prime, but obviously it did.
Correct way is to define the function in front of the solve block and use the function there.
As you can see in the pic below we get an even larger result if the values from the solve block are used in their full stored precision:
I have not looked in your sheet in detail and have not checked if you retyped the function definition correctly - maybe it would be worth doing so ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As you describe it it look s to me that a solve block seem to be the way to go.
You have to be aware that sometimes, depending on the nature of the equations, a solve block can be very sensible with respect to the the initial guess values.
If you experience trouble feel free to ask again but don't forget to attach your worksheet as well
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The attached worksheet (page 2) solves the equation from the initial post, but it does not appear to be for the maximum value of the function. For example, using different guess values and solving with the maximize function yields different results. Based on the published solution, the maximum value of the function for the given inputs should be in the range of 2.56 - 15.73 (8.00 for the example) ; however, the function value using the dependent variables in the worksheet is orders of magnitude greater than the solution. I will try adding a Solve block constraint restricting the range of values for the dependent variables to see if the solution can be restricted to the specified range.
I am also including the section from the text for information.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Based on the published solution, the maximum value of the function for the given inputs should be in the range of 2.56 - 15.73
And you got a value of approx. 2000. That means that "maximize" did a good job, doesn't it?
Which version of Prime the file was created in? After recalculation in Prime 9 I get an error message because maximize was used the wrong way. K.p is a constant (6.02) and you used it as a function. Actually I wonder why this worked in any version of Prime, but obviously it did.
Correct way is to define the function in front of the solve block and use the function there.
As you can see in the pic below we get an even larger result if the values from the solve block are used in their full stored precision:
I have not looked in your sheet in detail and have not checked if you retyped the function definition correctly - maybe it would be worth doing so ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Could not edit my posting above so I reply to it.
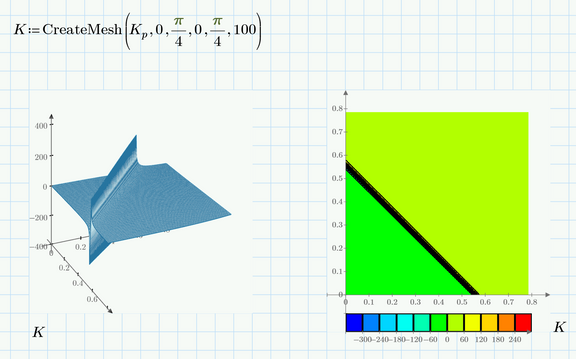
I plotted the function you defined and it looks like K.p can take values from minus infinity to positive infinity. Looks like rho+psi=~32 deg. This means that maximizing does not make much sense.
I limited both angles (rho and psi) to 0 to 45 deg in the plot.
So either there is a much more restrictive limit to the angles ar there is something wrong with the equation (either the one typed in your sheet or already the one published in the pdf).
EDIT:
I looked further in your equation and found this: