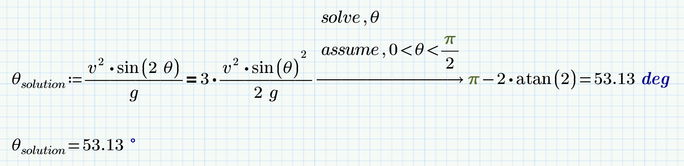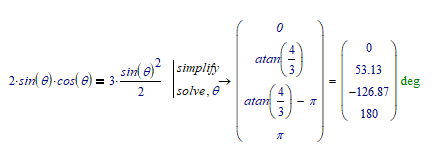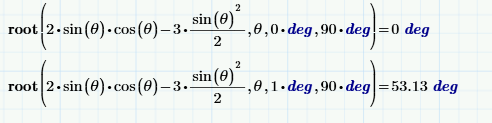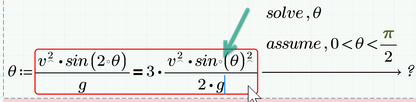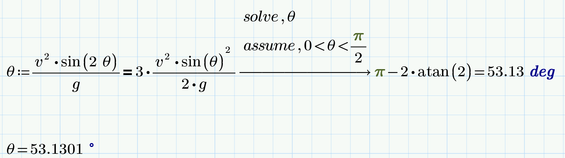Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@kenan2 wrote:
I don't understand how the equation can have different solutions when in the solution manuel is the answer: 53.1 deg.
The pure mathematical problem you posed first (the equation with trig functions) has an infinity number of solutions. But for your application I'd guess that only solutions in the range 0° to 90° (or 0 to pi/2) are physically relevant. So you have to tell Mathcad that you are only interested in solutions within that range. Trivially theta=0 is a "solution" to your problem, too, as Luc has explained, but sure not the solution you had in mind.
Then is seems you gave a wrong equation in your very first post with a superfluous factor 2. This equation would give you an angle of 69.44 °.
The equations you posted later seems to be the correct one.
So use this second equation, tell Mathcad via assumptions that you only are interested in solution within the aforementioned range and let Mathcad show the result in degree rather than the default radian and you get what you are looking for.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Don't only post a picture - additionally post you worksheet as it makes it easier for us to play around with and show you with your exact example what we are talking about.
@kenan2 wrote:
Hi.
How can i solve for the angle and get it into a number not a matrix?
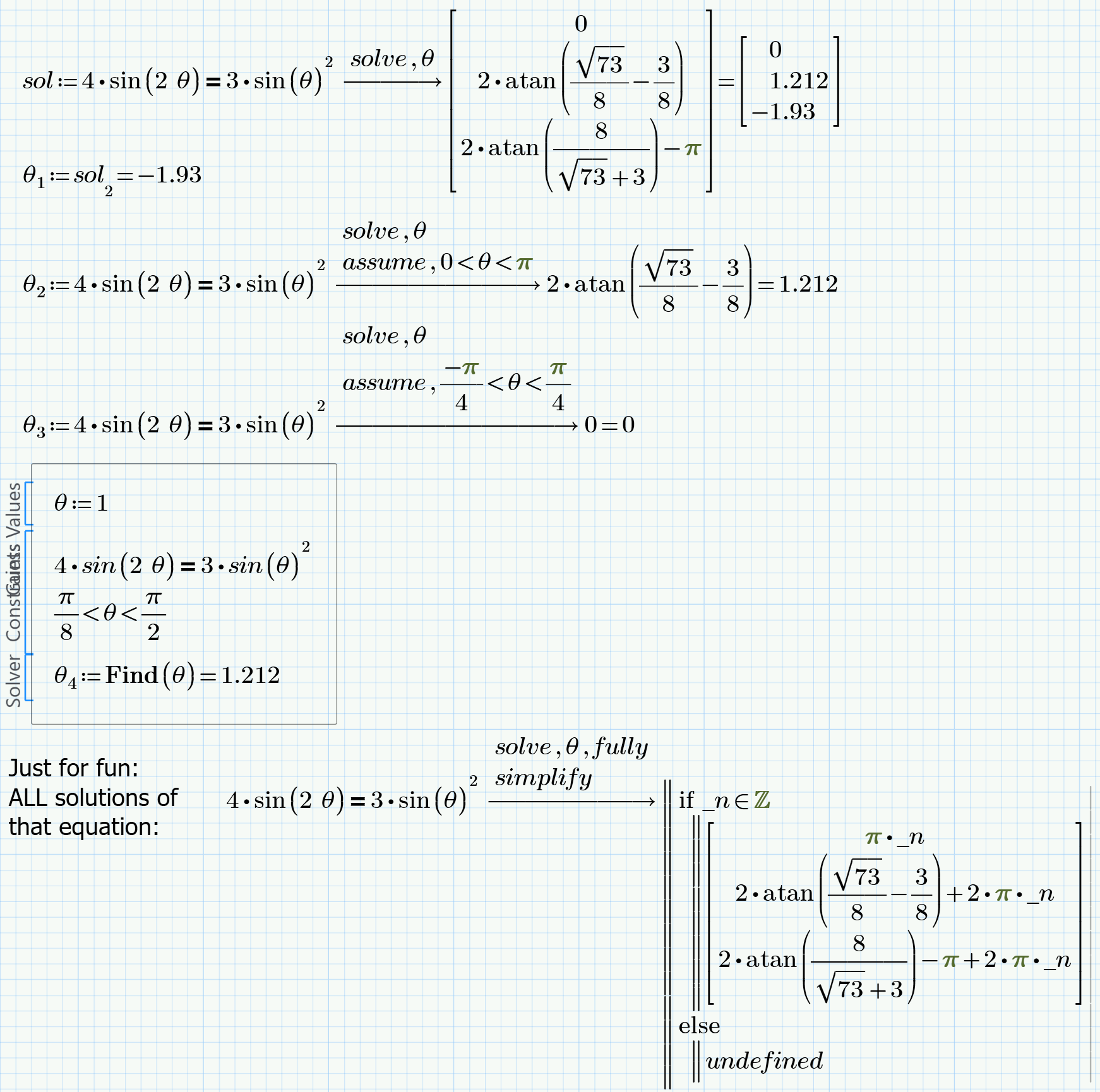
Your solution ARE numbers, but as there are more than one, Prime combines them in a vector.
Your equations has an infinite number of solutions. Mathcad shows you the three within the range [-pi; pi].
How should Prime know which of the solutions is the one you need if you don't tell it?
1) You may assign the outcome of the symbolic solve to a variable -> sol:=.... and then access the solution which is suitable for your application via vector index, e.g. theta := sol[2
2) You may use the assume modifier to only get the solution you are looking for, maybe like "assume, -pi<theta<-pi/2"
3) You may use a numeric solve block instead of the symbolic solve. Here you can apply additional constraints (like theta<0 or the like) and also control the outcome by using different guess values.
BTW, its expected of you that you come back to a question you asked and close the thread (e.g. by marking an answer as being correct or by assuming the question to be answered. And its not wrong to let people know if their answer had helped.
-> https://community.ptc.com/t5/PTC-Mathcad-Questions/Isolate/m-p/552340
-> https://community.ptc.com/t5/PTC-Mathcad-Questions/massflow-rate/m-p/549645
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hmm.. Do not understand 😕
Can Mathcad Prime not reduce it like that (SEE PICTURE).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@kenan2 wrote:
hmm.. Do not understand 😕
You have to be more precise as to what it is that you don't understand
Can Mathcad Prime not reduce it like that (SEE PICTURE).
I hope - NO! 😉
1) In your first line you already have lost a factor 2 as sin(2x)=2*sin x cos x
2) In your second line you divide by sin theta and so you are loosing all solutions which are multiples of pi ( ...,-pi, 0, pi, 2 pi, ...)
3) In your third line you divide by cos theta. Fortunately cos theta = 0 is no solution to your original equation. Nevertheless whenever you divide you have to make sure that you don't divide by zero.
4) arctan 4/3 = 53.31° is just one out of an infinite number of solutions of the equation tan x = 4/3. You may add (or subtract) any integer multiple of pi -> tan x = 4/3 => x = arctan (4/3)+ k*pi with k in Z.
But Prime's symbolics is far away from being perfect and the solution Prime is presenting to you sure could be simplified but muPad (the symbolics in Prime) seems not to be to convinced to do so.
The solutions to your equations are:
a) any integer multiple of pi -> k*pi with k in Z
b) arctan(8/3) + k * pi with k in Z
The expression Prime gives you is more complicated but its perfectly equivalent.
And at last again: Your equation has an infinity number of solutions. If you expect a specific one (maybe 69.444°) you will have to tell Prime so (e.g. via the assume statement). If you want to see the angle)s= in degree, you simply have to type deg or ° in the placeholder after the result values. Using the degree character ° is more complicated in Prime than it is in real Mathcad - you can't use the keyboard to type it in but must chose it from the "Units" dropdown.
As you can see in the picture Prime delivers the very same result in a quite different notation if we rewrite the equation with tan functions before we solve it. I was not able, though, to convince Prime to simple give us atan(8/3) which would be the most simple way to write that solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't understand how the equation can have different solutions when in the solution manuel is the answer: 53.1 deg.
And here is the problem i need to solve.
A projectile is fired in such a way that its horizontal range is equal to three times its maximum height. What is the angle of projection?
I know how to solve it on papir, but I want to know how I can get to the answer 53.1 deg in Mathcad. Can you please only tell me that thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As Werner explained, the solution you have is not the only one, given the problem as it is stated.
Another perfectly fitting solution is the theta=0, That gives a height of 0 and a distance of 0. 3*0=0. Perfectly fits the problem description. But by division with sin(theta) you threw that solution away implicitly, because then you would be dividing by sin(0)=0 ...
What you want is the smallest, non-zero solution.
You'll have to pick it from the list of solutions, or instruct mathcad to use assumptions on the answer.
If all you want is the numeric answer, you could also use the root function, which produces only one answer in numerics mode. And you can easily set the range in which you want the answer:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@kenan2 wrote:
I don't understand how the equation can have different solutions when in the solution manuel is the answer: 53.1 deg.
The pure mathematical problem you posed first (the equation with trig functions) has an infinity number of solutions. But for your application I'd guess that only solutions in the range 0° to 90° (or 0 to pi/2) are physically relevant. So you have to tell Mathcad that you are only interested in solutions within that range. Trivially theta=0 is a "solution" to your problem, too, as Luc has explained, but sure not the solution you had in mind.
Then is seems you gave a wrong equation in your very first post with a superfluous factor 2. This equation would give you an angle of 69.44 °.
The equations you posted later seems to be the correct one.
So use this second equation, tell Mathcad via assumptions that you only are interested in solution within the aforementioned range and let Mathcad show the result in degree rather than the default radian and you get what you are looking for.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its hard to debug a picture - we don't even see what the error message is telling you.
Best guess is that you had assigned theta a value before.
If thats true you get an error as of an invalid solve variable.
Fix in this case is to undefine/clear theta.
Before the solve region you write clear(theta) or clear.sym(theta)
If this is not the cause of your problem you'll have to attach your worksheet here (which would have been a good idea anyway from beginning).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As Werner already wrote: PLEASE attach your worksheet (rather than just a picture.).
There's something wrong with your 'sin(q)^2', it looks like the 'sin' got detached from its argument '(q)^2'. It shows like 'sin (q)^2', rather than 'sin(q)^2'.
Did you perhaps first type the '(q)^2' and then put a 'sin' in front of it?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think Luc is right with his guess. Well observed!
If you would have assigned theta a value before, the red error rectangle would be around the word "solve" and not around the whole expression.
So delete the (theta)^2, put the cursor right after the n of sin and retype (theta)^2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
which n ??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@kenan2 wrote:
which n ??
The n of the word sin 😉
You still have not attached your worksheet (why???)so unfortunately we can only guess.
As Luc noted it looks like you created "sin times (...)" instead of "sin of (...)".
But of course we can't be sure without seeing your worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When you click in the region you see a tiny implicit multiplication sign between "sin" and "(...".
This proved that Lucs observation was correct.
Delete that multiplication and it works:
Worksheet in format P4 attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Okay same problem again...
How can I solve for the angle ?
It do not work if I use same princip.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess you should solve a system of equations for theta and F.snor, right?
I'd suggest a numeric solve block
Worksheet in format P4 attached