Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Study-16
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Study-16
The page of the Study 16 of the book 2^5 Problems for STEM education
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Having followed the chain of messages from the "continue" thread, I thought I'd Expressify the calculation using Werner's recently discovered, undocumented, built-in function update1.
A somewhat meandering Mathcad Express 7 worksheet is attached - I was just putting stuff down as it occurred to me.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Didn't you intend to replace the 10^5 in the definition of" NDice" for the third function argument "n" ?
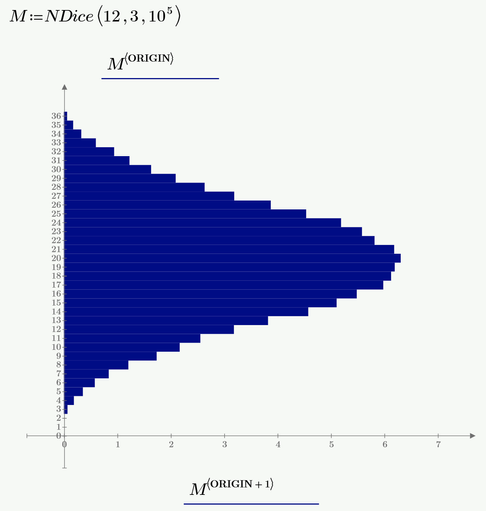
BTW, here's a first attempt for a graph showing the rolling of three dodecahedrons.
I had a "great" time formatting the display because of Primes idiotic implementation for resizing matrices 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
Didn't you intend to replace the 10^5 in the definition of" NDice" for the third argument "n" ?
Yes. Well spotted.
Cut & Paste Error, of course. ☹️
It was a bit of a rush job and I didn't have time to review it properly ... although, I still might have missed it. I don't normally spot errors until after I've posted a worksheet, anyway. 😁
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Instead of the output shown above, I sure would prefer something like seen in the picture below, but I am not well versed enough in "programming" in Prime Express to do it,
But of course we always can use Prime's "outstanding" plot skills
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
BTW, here's a first attempt for a graph showing the rolling of three dodecahedrons.I had a "great" time formatting the display because of Primes idiotic implementation for resizing matrices 😞
Hah Hah! 😂 Been there, done that, burned the T-shirt, stuck pins in a voodoo doll of whoever thought it was a good idea to manually expand a large nested array.
BTW, here's a first attempt for a graph showing the rolling of three dodecahedrons.
Left-/right-justifying nested arrays is yet another item on my feature request list. ☹️
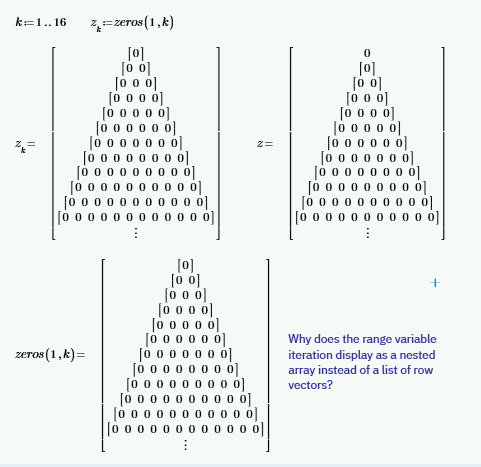
I wondered if iterating over a range variable might look better. It doesn't.
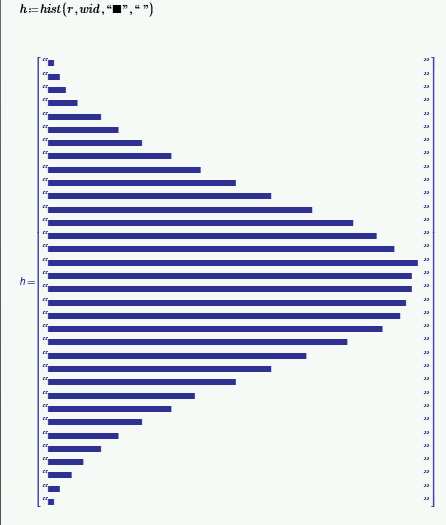
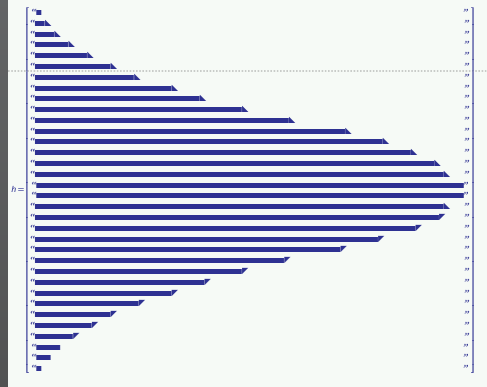
I then wondered if a stringogram would look any better ...
(I'm lacking the energy and will-power to build the scaling into hist)
I found a larger filled square character but not a matching space character.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
(I'm lacking the energy and will-power to build the scaling into hist)
A nice cup of tea has wonderful restorative powers.
I found a larger filled square character but not a matching space character.
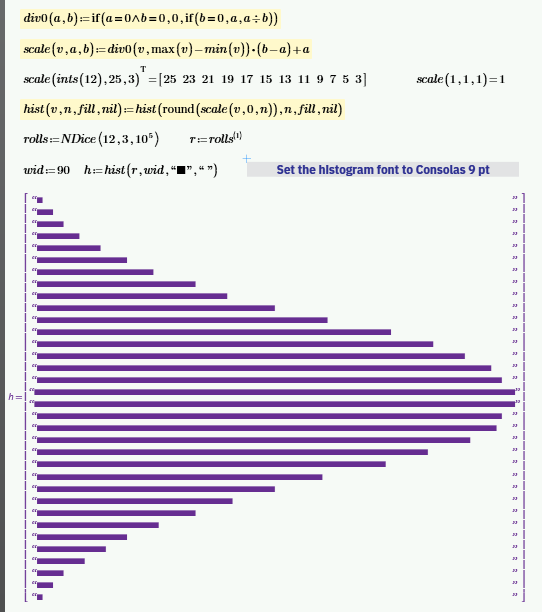
The best I could manage was contrasting characters. Not sure it was worth the effort.
I was toying with the idea of using half-filled diagonal characters to improve the appearance of the slopes. But I'd run out teaspiration, but after another cup of tea, I managed to sort of do it. Not sure it was worth the effort, either. I feel like I'm back in the days of ASCII Art.
"Normal"-sized characters don't quite align properly with the filled-diagonal characters.
I don't suppose I need to say that some form of String Markup Language (RTF, HTML, whatever) has been on my feature request list since pterosaurs first took to the air, do I? Oh, and the ability to lose the quote marks - they're usually far too obtrusive for my needs.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
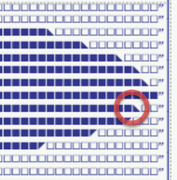
Wow! Really great job, indeed. I'm just wondering if I should switch from coffee to tea 😉
BTW, the encircled diagonal character - isn't it the wrong one?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks to all!
Or you can please analyze for new book the second, more difficult problem of this chapter of the old book - the problem of a three-way duel - see attach. I need more interesting? more short solusion!
The rnd function we used to toss the coin and the dice will also help us solve the problem of a three-way duel on the computer.
Sam, Bill and John agreed to fight in a three-way duel by the following rules:
- a draw determines who fires the first, second and third;
- duelists are located at equal distances from each other (at the corners of an equilateral triangle);
- they exchange shots in turn, determined by fate, until two are killed;
- whoever is next to fire can shoot at any of the living duelists.
It is known that Sam is a sniper and never misses from this distance, Bill hits the target in 80% of cases, and John in 50%. What is the best strategy for each participant and what are the chances of their survival if they follow the best strategies?
In this duel, Sam (the sniper) and Bill (a good shooter) can adopt one of two tactics of behavior, namely, random, when the shooter knows nothing about the accuracy of the opponents and fires at the first determined by the throw of a coin. The second tactic (most accurate), when the duelist is aware of which of his opponents shoots better, and he aims at the opponent with the higher accuracy in the hope of remaining head-to-head with the worse shooter.
John can follow another, third, “tricky” tactic. To get the highest chances of winning the duel, he must deliberately shoot avoiding the target while his two rivals are alive. After all, the next shooter, if he adheres to the tactics of “beat the most accurate”, will fire not at John, but another opponent. After Sam or Bill is killed, John must show all he is capable of. In this situation, his chances of survival are 50% if he was alone with Sam, and more than 50%—if with Bill. And as a result, the chances of surviving from John will be higher than that of Sam and Bill.
Let’s simulate this three-way duel on the computer. The participant of the duel, before shooting, must, first, identify the more accurate opponent, adhering to the tactics of “beat the most accurate”. For this purpose, the MostAccurate function is used, which returns the number of the enemy with the highest rifle qualities. In it, by looking through all the participants in a duel (the for loop), only the living opponents are taken into account, of course (Status Target = “alive”) and not the shooter himself (Target ≠ Shooter).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
Wow! Really great job, indeed. I'm just wondering if I should switch from coffee to tea 😉
You seem to be doing just fine on coffee, Werner. 😎
BTW, the encircled diagonal character - isn't it the wrong one?
Look, if I need criticism, I'll ask my wife! I knew it wasn't worth it. 👿
No, it's the right character. It merely happens to be in the wrong place. It can happen to the best of us. 😇
Unfortunately, you've opened a can of worms. What I'd intended as a simple demonstration has now escalated into a full-blown development, with functions and stuff, instead of just a simple range-variable scan of the "histogram".
Even more unfortunately, it's never the rarely the heart of the problem that's an issue, it's the edge cases.
I thought I'd semi-fixed the algorithm,
but, no,
I hate edge cases; they have a nasty habit of ruining the elegance of an algorithm. 😭
Luckily, I have the mind of a grasshopper and will have moved onto crops anew before I've finished dealing with them.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
PTC Mathcad Community in XVII century
See more
Игроки в кости: 2 тыс изображений найдено в Яндекс.Картинках (yandex.ru)