Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Study4
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Study4
Этюд 4. Решатели или Великолепная семерка Mathcad
В этюде рассказано, какие средства есть у математического пакета Mathcad для решения уравнения и систем уравнений, какие есть уравнения, как они решались в докомпьютерную эру и как они решаются сейчас.
Файлы с задачами этюда в аттач здесь и в последующих реплика.
- Labels:
-
Other
- Tags:
- group discussion
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Очередные файлы с задачами этюда в аттач
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Рисунки этюда (файлы см. выше)
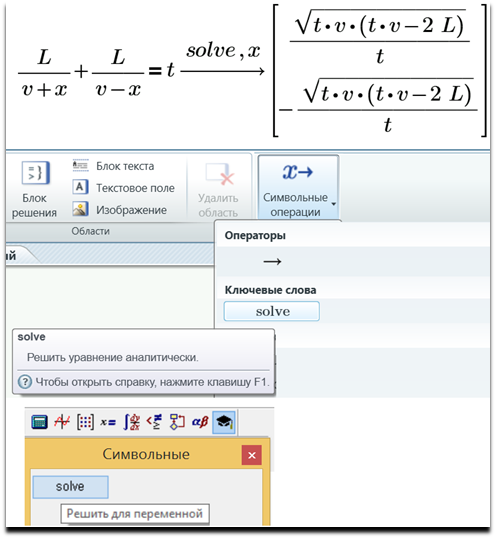
Рис. 4.1. Аналитическое решение задачи о движении моторной лодки (Mathcad Prime)
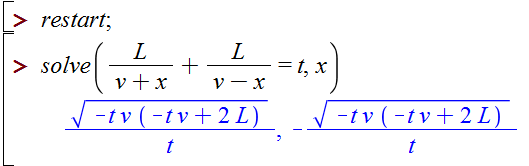
Рис. 4.1a. Аналитическое решение задачи о движении моторной лодки (Maple)
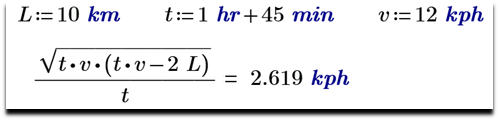
Рис. 4.2. Решение задачи о моторной лодке по найденной на рис. 4.1 формуле

Рис. 4.3. Поиск корня уравнения: очень объемный скрытый ответ

Рис. 4.4. Поиск корня уравнения: решение не найдено
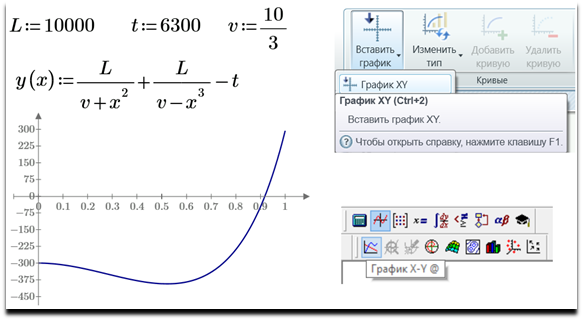
Рис. 4.5. Графический поиск нуля функции

Рис. 4.6. Работа в среде Mathcad встроенной функции root с четырьмя аргументами
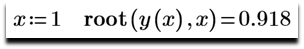
Рис. 4.7. Работа в среде Mathcad встроенной функции root с двумя аргументами
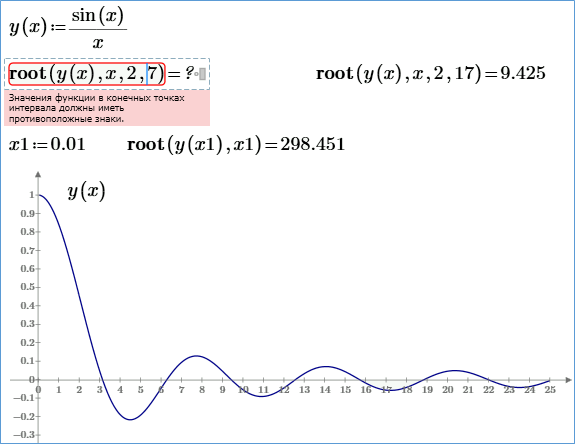
Рис. 4.8. Особенности работы двухаргументной функции root

Рис. 4.9. Численный ответ символьного оператора

Рис. 4.10. Графическое и численное (через функцию root) решение задачи о моторной лодке

Рис. 4.11. Определение коэффициентов полинома
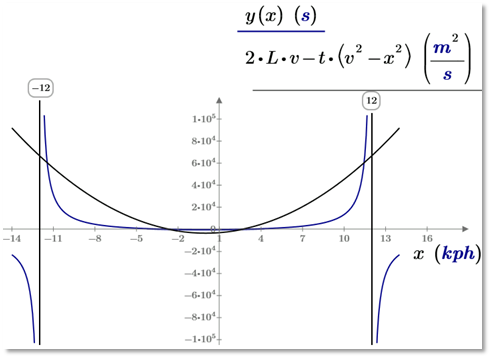
Рис. 4.12. Исходное и квадратное уравнение движения моторной лодки

Рис. 4.13. Поиск нулей полинома в среде Mathcad

Рис. 4.14. Решение уравнения золотого сечения в среде Mathcad

Рис. 4.15. Решение систем уравнений с помощью функции Find
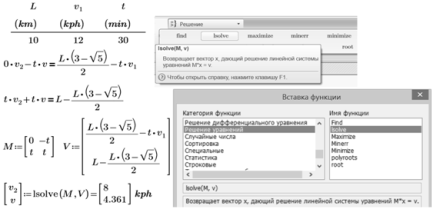
Рис. 4.16. Решение СЛАУ в среде Mathcad
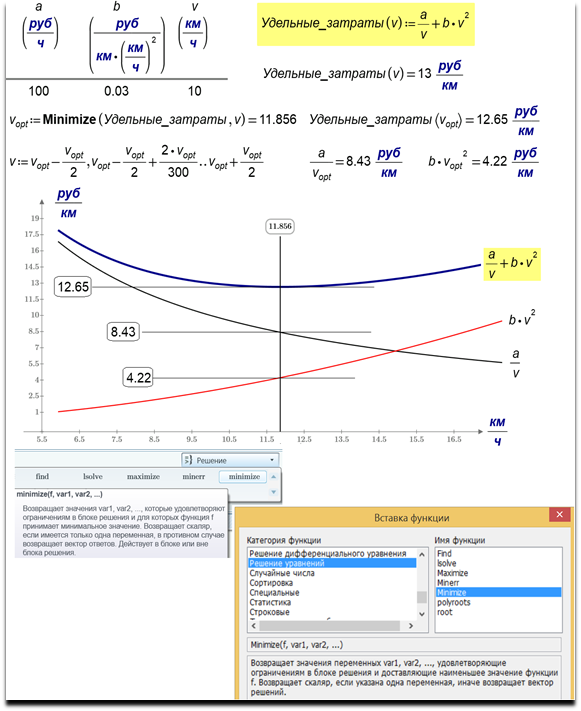
Рис. 4.17. Нахождение крейсерской скорости судна численной математикой Mathcad
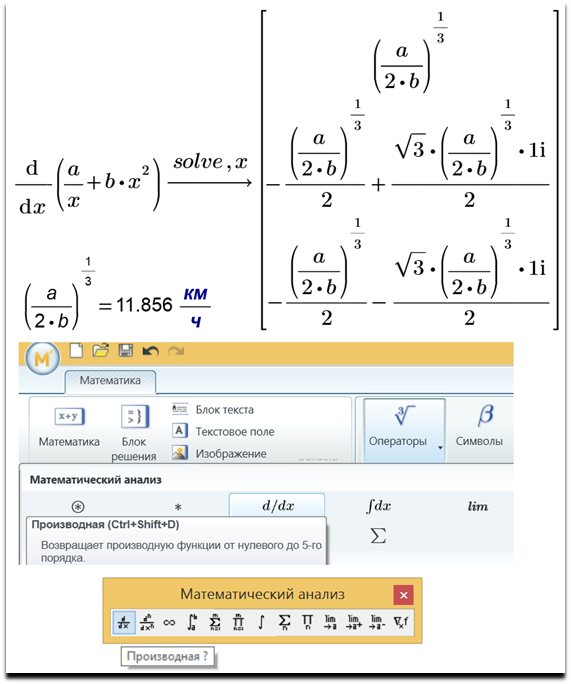
Рис. 4.18. Нахождение крейсерской скорости судна символьной математикой Mathcad

Рис. 4.19. Осечка при работе с символьной математикой Mathcad
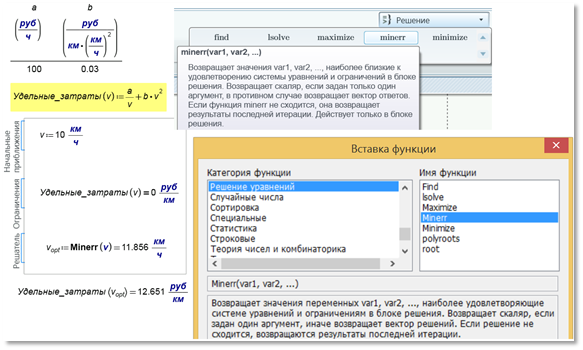
Рис. 4.20. Решение задачи оптимизации с помощью функции Minerr
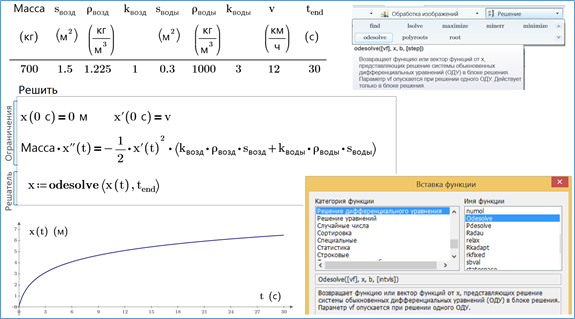
Рис. 4.21. Решение задачи об остановки лодки
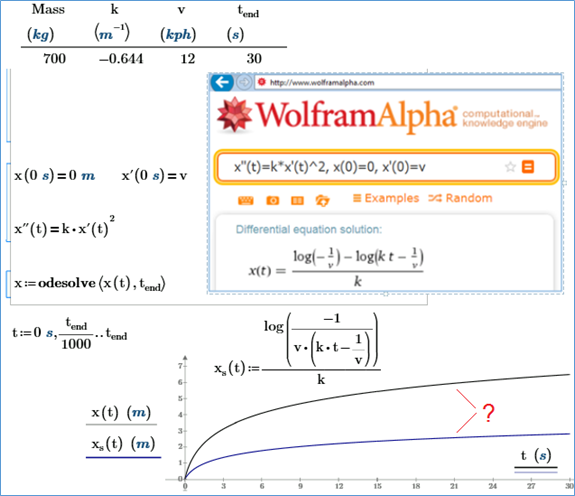
Рис. 4.22. Графическое сравнение аналитического и численного решения ОДУ
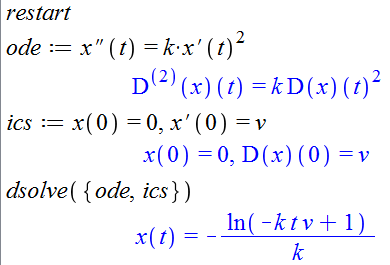
Рис. 4.22a. Аналитическое решения ОДУ в Maple
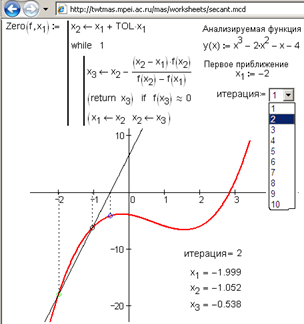
Рис. 4.23. Метод секущих: анимация Video Link : 1411 online расчет: http://twt.mpei.ac.ru/mas/worksheets/newton.mcd и http://twt.mpei.ac.ru/MCS/Worksheets/Math/Newton.xmcd

Рис. 4.24. Трассировка двухаргументной функции root
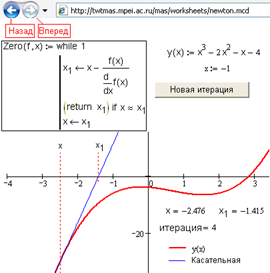
Рис. 4.25. Метод Ньютона: анимация Video Link : 1466 online расчет: http://twt.mpei.ac.ru/MAS/Worksheets/secant.mcd
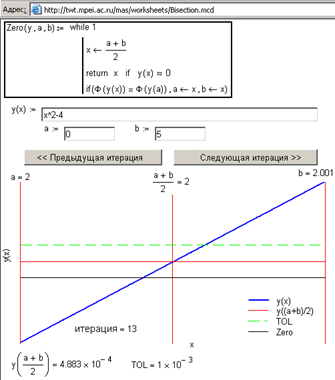
Рис. 4.26. Метод половинного деления: анимация Video Link : 1468 online расчет http://twt.mpei.ac.ru/mas/worksheets/Bisection.mcd
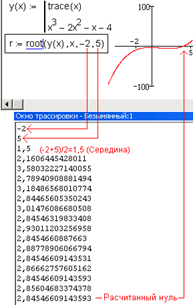
Рис. 4.27. Трассировка четырехаргументной функции root

a)

a)
c)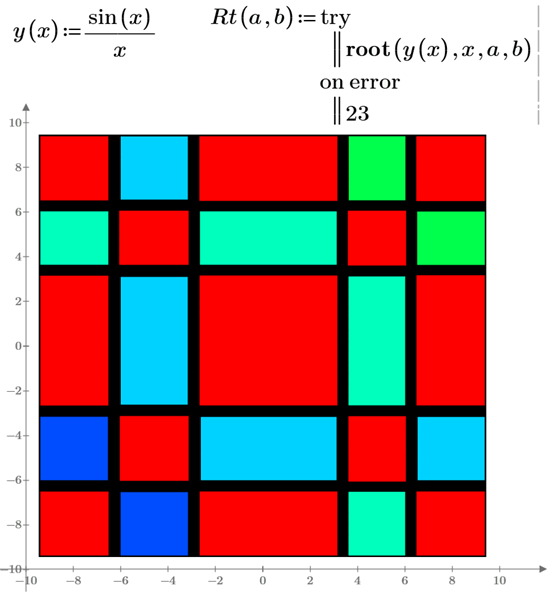
Рис. 4.29. "Отпечаток" нулей четырехаргументной функции root:
a) Mathcad 11; b) Mathcad 12-15; c) Mathcad Prime 3

Рис. 4.30. Решение обратной задачи с использованием функции root
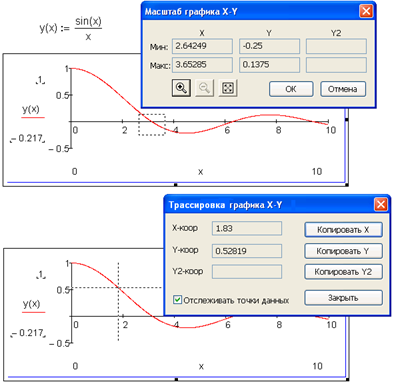
Рис. 4.31. Уточнение нулей с помощью графики
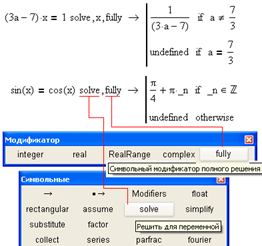
Рис. 4.32. Поиск всех нулей функции средствами символьной математики

Рис. 4.33. Полное решение системы двух нелинейных уравнений с помощью функций Find
при ее аналитическом вызове (Mathcad 11/12/13)
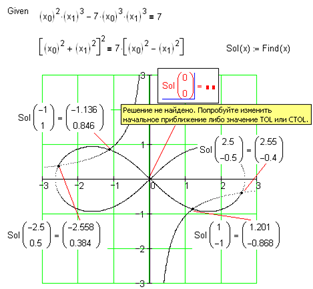
Рис. 4.34. Решение системы двух нелинейных уравнений с помощью функций Find
при ее численном вызове

Рис. 4.35. Решение системы двух нелинейных уравнений с помощью функций Find
при ее аналитическом вызове (Mathcad 14/15)
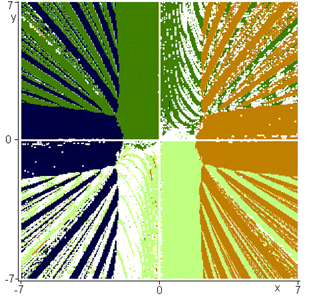
Рис. 4.36. "Картинка" численного поиска корней системы двух нелинейных алгебраических уравнений по алгоритму Левенберга — Маркворта

Рис. 4.37. Винсент Ван Гог "Пейзаж в Овере после дождя"
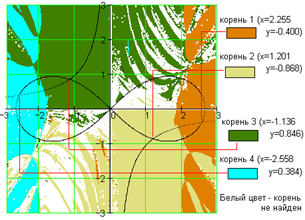
Рис. 4.38. "Пейзаж" численного поиска корней системы двух нелинейных алгебраических уравнений
с наложенным графиком уравнений
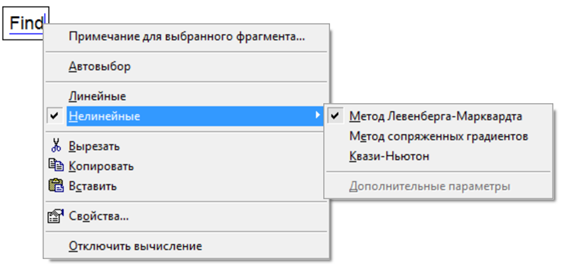
Рис. 4.39. Выбор метода решения системы нелинейных алгебраических уравнений

Рис. 4.40. "Пейзаж" численного поиска корней системы двух нелинейных алгебраических уравнений
по алгоритму сопряженных градиентов

Рис. 4.41. "Пейзаж" численного поиска корней системы двух нелинейных алгебраических уравнений
по квазиметоду Ньютона

Рис. 4.42. "Пейзаж" численного поиска корней системы двух нелинейных алгебраических уравнений
по алгоритму Левенберга — Марквардта с повышенной точностью

Рис. 4.43. Программа сканирования корней уравнения
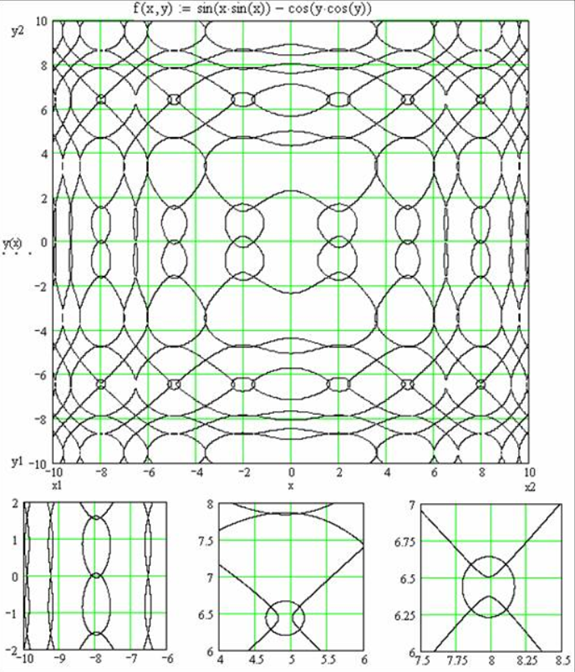
Рис. 4.44. Салфетка, сплетенная компьютером
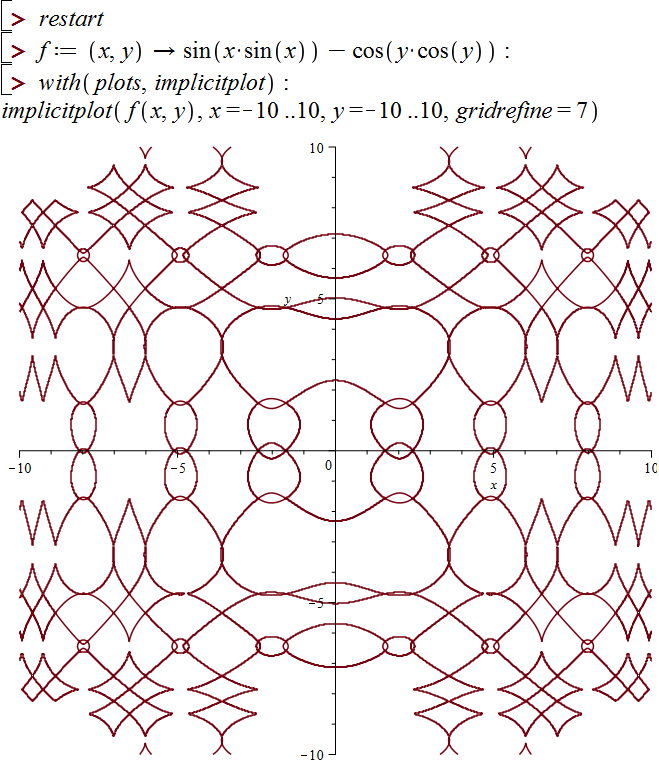
Рис. 4.44a. Построение графика f(x, y) в среде Maple

Рис. 4.45. Салфетка, сплетенная компьютером (вариант 2)
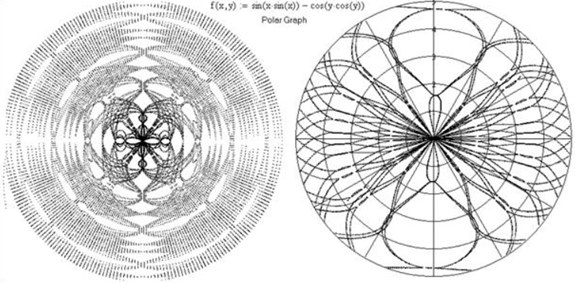
Рис. 4.46. Кружевная салфетка в полярных координатах

Рис. 4.47. Цветная программа сканирования неравенства
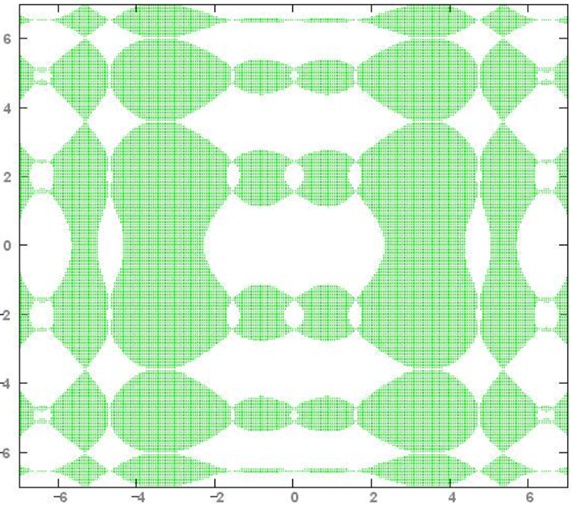
Рис. 4.48. Компьютерная вышивка Ришелье
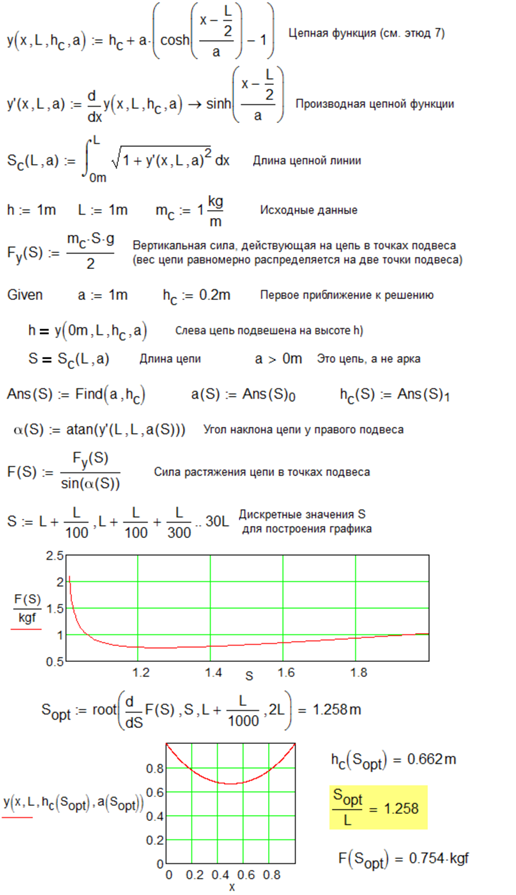
Рис. 4.49. Создание функции пользователя с опорой на функцию Find

Рис. 4.50. Упрощение задачи об оптимальной форме цепи (неудачное использование функции root)
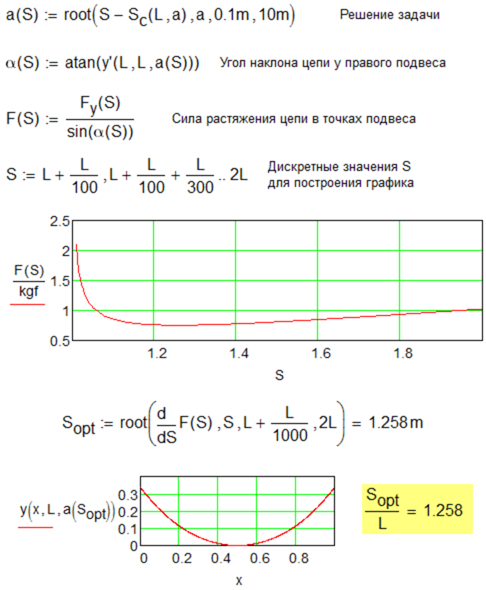
Рис. 4.51. Упрощение задачи об оптимальной форме цепи (удачное использование функции root)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Задача 1.
Парусная лодка прошла по озеру в одно сторону S=15 км., по направлению ветра, а потом вернулась в исходную точку. Весь этот путь занял 3 часа 30 минут. Какова скорость ветра Vв, если собственная скорость лодки V=10 км/ч ,а направление ветра не менялось?(С помощью функций:Root,Polyroots)
Задача 2.
От двух пристаней на прямолинейном участке озера одновременно отходят две парусные лодки и плывут навстречу друг другу. Причем первая лодка плывет по направлению ветра, а вторая против. Они встречаются в точке, делящей этот участок озера в соотношении золотого сечения. Найти скорость второй лодки V2 и скорость ветра Vв, если скорость первой лодки V1=12 км/ч. Расстояние между пристанями S=15 км, а время движения лодок до встречи равно t=45 минут.(С помощью функций:Find,Isolve)
Задача 3.
Задача о плане выпуска лодки двух моделей.(С помощью функции Maximize)
Задача 4.
Определить скорость производства лодок – скорость, при которой затраты на их эксплуатацию будут минимальны.(С помощью функции Minimize)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
About the magnificent 5,6 and 7 (Minimize,Maximize and Minerr), In mathCAD 15 the user could opt for Linear and Nonlinear, and in case of Nonlinear select among Levenberg-Marquardt, Conjugate Gradient and Quasi-Newton. Are the same methods available in MathCAD Prime ? Are all these methods sensitive to the guess/initial values?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator





