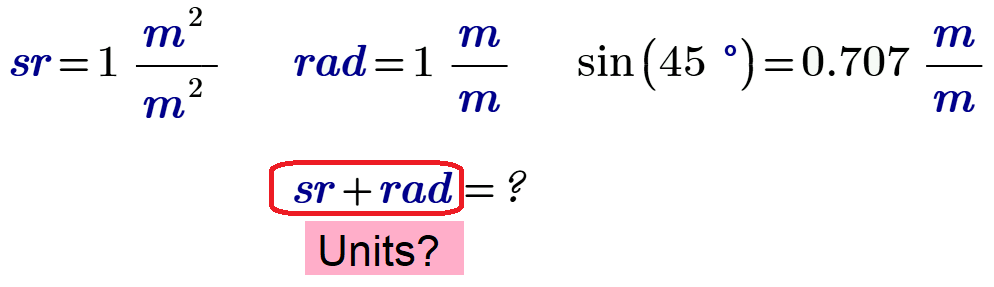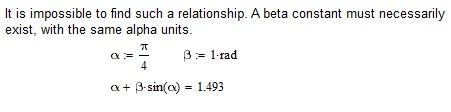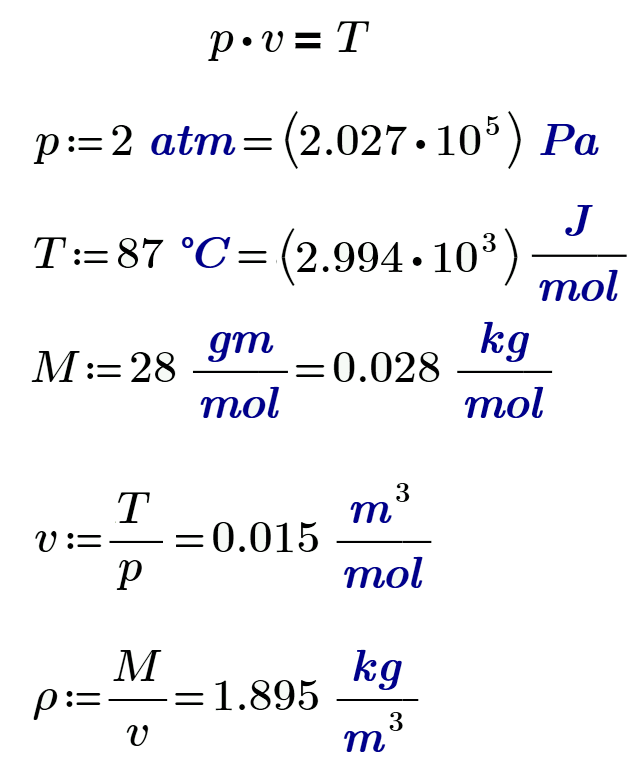Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
SuperMathcad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SuperMathcad
Fig. 1
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fig. 2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Only if one accepts that an angle *is* just the ratio of two lengths ... which hypothesis somewhat defies the observations of our eyes.
I prefer an alternative hypothesis in which the quantity angle is a base dimension within a system of units. This, to my eyes, makes more physical sense (how else does one capture the physical notion of rotation?). The maths works out, ... it's just that most people won't like the 'New Units Maths' because it changes how they would do dimensional analysis.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>Only if one accepts that an angle *is* just the ratio of two lengths
Point please second!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
radians.
😈
Stuart
(seriously)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just like MFra, I find the same type of expected, error-free result ONLY when I use Mathcad 15...ah the good ol' days...😎
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think one thing that seems to have been lost is the desire to make Mathcad much better, not just live in hope that Prime will be as good as M15 one day. Ah well.
I do wish they'd left partial application in. It would have made working with Prime *so* much easier.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Could you please tell me what you mean by partial application in Mathcad? How is it missing in Prime?
Many thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Partial Application is where you can take a multi-argument function and construct a new function by assigning a value to one or more of the leading arguments but not all of them. For example, in Mathcad 15 you could write
| Define a two-parameter function power (same as exponentiation operator) | power(x,y) := x^y |
| Define function Bin to raise 2 to the power of y by partially applying power to 2 | Bin := power(2) |
| Evaluate Bin like any other 1-argument function | Bin(8) = 256 |
Once you get used to how it looks, it's very useful for abbreviating function definitions, particularly so when, say, you have a 3+ argument function with the last two arguments being x & y or i & j and can then set the leading arguments when, say, using it into a 3D plot.
Another example to help make its utility clearer. The built-in function matrix(m,n,f) takes two integers m & n and a two-argument function f(i,j). matrix iterates over the matrix indices i = 0 .. m-1 and j = 0.. n-1, generating a matrix whose elements are f(i,j).
succ(m,i,j) := i + m*j
M(m,n) := matrix(m,n,succ(m))
M(3,3) should create a 3x3 matrix of column-wise successive integers.
If you have programming, it could be done using a local function definition
M(m,n) := matrix(m,n,f(i,j)<-succ(m,i,j))
But I think the latter is less 'succ'inct and harder to read, particularly when there are long names or even expressions for the arguments, or multiple functions in a plot.
Unfortunately, Prime doesn't do it, nor, whilst I'm having a moan, does Prime allow local functions to be recursive; Mathcad 15 provided both these features.
PTC deliberately removed partial application because it confused somebody when they left an argument out of a function <Sigh>. So we have a mathematical application removing a facility that every other programming language and their dogs are busy implementing ...
I think the lack of local recursion is just a specification / programming mistake.
Regardless, I have a number of useful worksheets that are now broken. I could do a lot more with Prime (especially Express) if it had both.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is an example. In general, the individual terms of a polynomial (linear and non-linear), if they are dimensionless, everything is ok. But if one of them has units of measurement (for example the rad), then there must be homogeneity between the various terms (this is obvious). So if alpha is in radians and is added to something, this something must also be in radians (this too is obvious) and since sin (alpha) is dimensionless, it must necessarily be multiplied by a constant or a variable ( with the same dimension as alpha) which makes the term homogeneous with the others. Another example is the following relating to a differential equation:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
It is an example. In general, the individual terms of a polynomial (linear and non-linear), if they are dimensionless, everything is ok. But if one of them has units of measurement (for example the rad), then there must be homogeneity between the various terms (this is obvious).
Agreed.
So if alpha is in radians and is added to something, this something must also be in radians (this too is obvious)
Also agreed.
and since sin (alpha) is dimensionless,
But here's where we probably diverge. Why do you think that sin(alpha) is dimensionless?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry,
What a (physical) meaning in this formula?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I didn't explain myself well!
that is a useful example to highlight the homogeneity of the units of measurement of the terms of an equation (in this case differential). This equation allows us to determine the effect of an electromagnetic field with pulsation omega0, in interaction with a particular medium. It polarizes a certain number of atoms or molecules creating electrical dipoles and therefore some dipole moments, it follows that the polarization of the same varies. The differential equation, therefore, allows us to determine the temporal trend of polarization. It must be associated with another differential equation relating to the concentrations of dipole moments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry but the state equation of perfect gases is: PV = nRT. So it is not clear to me what you write.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry the state equation of perfect gases is pV=T.
R is a coefficient between J/mole (a base unit of temperature) to K (one others unit of temperature).