Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
The usual problem with the imaginary unit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The usual problem with the imaginary unit.
Hello everyone,
What can I do to prevent this?
in order to have a result, I had to consider the operators as variables.
Thank you for all.
F. M.

Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

This ist the first time in the sheet you show where you are using complex entries and so its the first time you experience the difference between conjugate or not.
I am not willing to retype but I guess you would get the result you expect if you use one of the two methods I showed above (transpose the first factor OR conjugate the second).
Regards, Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is what it looks like in Mathcad 11:
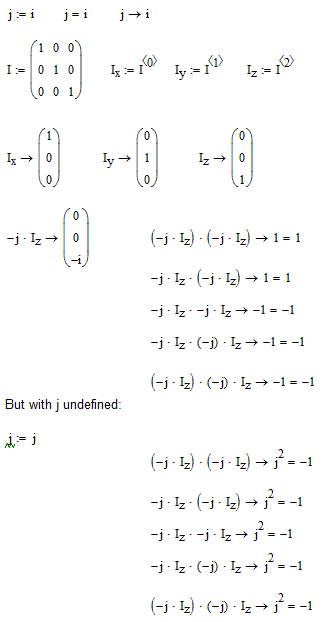
(I was wondering why you got j instead of i in the result:

That happens only if j is symbolically undefined.)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
(I was wondering why you got j instead of i in the result:
That happens only if j is symbolically undefined.)
No, you can switch between i and j in the result format dialog:
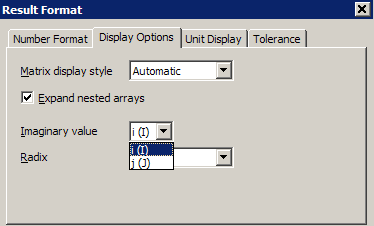
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That option is available in Mathcad 11, but it doesn't affect the symbolic results, only the numeric:
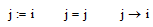
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure why you think that Mathcad is doing anything wrong.
It correctly complies with the definition of the dot product of vectors with complex entries:

See here, for instance: -> Dot product - Wikipedia, the free encyclopedia
To get what you obviously want to see, you would either have to use the matrix product (multiply a 1x3 row vector with a 3x1 column vector) or use the conjugate of the second vector of the dot matrix produkt:
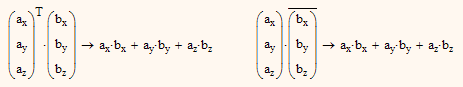
So for your first "wrong" example:

> > in order to have a result, I had to consider the operators as variables.
Sorry, but I don't understand what you mean by that!?
Regards Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

Thank you for your kind attention and response that will be, definitely, the right one.
heartfelt greetings
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

This ist the first time in the sheet you show where you are using complex entries and so its the first time you experience the difference between conjugate or not.
I am not willing to retype but I guess you would get the result you expect if you use one of the two methods I showed above (transpose the first factor OR conjugate the second).
Regards, Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner, you're right, it was a distraction not considering the complex conjugate. You have solved the puzzle.
You are the best!





