Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Thermodynamic Problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thermodynamic Problem
Hello to all,
I am having another 'simple' moment where I am going round in circles and am starting to feel a bit dim.
In the attached is a simple thermo question I am trying to complete.
I have completed a-c with some ease but am struggling with d. where the hint is to evaluate the integral of pressure over dVolume in the associated Pressure/Volume graph.
I know that the integral of an isothermal expansion is either P*V*In(r) = heat supplied or m*R*T*In(r)
Where P and V are the initial (Pre-expansion) Pressure and Volume respectively and r is the ratio of expansion i.e. V2/V1. m being mass and R being the gass constant.
As all figures given are specific i.e. no mass of air is specified I don't beleive I can use mRTIn(r) but cannot evaluate PVIn(r) as I don't know what the initial volume is...
I know that the heat supplied (well my calculations beleive it is) 187.5 kJ/kg.
I beleive the approach is to calculate the volumes from the integral and then with this to find the pressure noting PV/T = Constant.
Any help, as always, really appreciated.
Andy
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry I should have added:
P1 = 800 kN/m^2
T1 = 750 K
R = 0.287kJ/kgK
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And I am obviously trying to find P2 and to do that beleive I need V1 and V2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So after some further thought, I have an approach but would appreciate someone wiser than I validating this approach...
Noting that I have the heat input to the isothermal expansion which is in kJ/kg I have negated m (kg) from the integral mRTIn(r) which would give a result in kJ/kg which is what I am after.
Then I can manipulate RTIn(r) to isolate In(r). Then by evaluating e to the power of the result of In(r) should give me r i.e. the expansion ratio i.e. V2/V1. This should then be an identity with P1/P2 noting P1*P2 = V1*V2 and I can then isolate P2 noting I have P1.
Any thoughts?
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How about a Mathcad sheet...?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
Yeah Sorry that would be logical. I have been without MC today and working by hand would you beleive. I should be up and running electronicly tomorrow.
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok, let's see the "by hand"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Definately is 'Homework'.
I am not about cheating, I am all about learning as you hopefully know by now.
So where I have got to:
I have crudly sketched a PV and a TS diagram and have calauated as follows.
Known values:
R= 0.287kJ/kgK
Change in Entropy (in Expansion which should also be the same for Contraction)
Delta s = 0.25 kJ/kg
Net Work W = 100 kJ/kg
Aboslute Temperature at point 1 on a PV diagram i.e. before isothermal expansion = 750 K
Pressure at point 1 = 800 kN/m^2
My first step was to find the lower temperature and amount of heat rejected during isothemal compression. I note that the area of the square created in a TS graph will equal the net work. i.e. the product of change in entropy and change in temperature will be the net work. Therefore dividing the net work by the change in entropy should give the change in Temperature i.e.
Delta T = W/Delta s = 100 kJ/kg / 0.25 kJ/kgK = 400 K.
Ergo T2 i.e. lower Temperature = T1 - Delta T = 750K - 400K = 350K
Next I note that the heat rejected by the cycle in isothermal compression is equal to the product of the Temperature (T4) after compression the change in entropy. i.e.
Qc = T4*Delta s = 350K*0.25kJ/kgK = 87.5 kj/kg
To verify this I looked at the heat taken in during isothermal expansion as Qh = T1*Delta s = 750K*0.25kJ/kgK = 187.5kJ.
This holds true with the first law i.e. Sum of Q = Sum of W noting heat in is positive and heat out is negative
187.5 + (-87.5) = 100
Then the thermal Efficiency being T1-T2/T1 = 750-350/750 = 0.53 (reocurring).
Then I move onto the final part which I am not sure about.
I note that the isothermal work done in expansion is an identity with the heat taken in.
The heat taken in Qh = mRT1In(r) Noting this problem is in specific terms I have negated m as mass of air is not given (as a punt although the units come out as desired following this approach).
Ergo:
187.5 kJ/kg = R*T1*In(r)
= 0.287*750*In(r)
187.5 =215.25*In(r)
0.871=In(r)
0.871= log (base e) (V2/V1)
e^0.871 = V2/V1
e^0.871 = 2.389
Then I have taken that for an isothermal process P1*V1/T1 = P2*V2/T2. T will cancel as Temerature is constant in an isothermal process leaving P1*V1 = P2*V2
This can then be rearanged to give P1/P2 = V2/V1
Ergo: P1/P2 = 2.389
As I have P1 (800 kN/m^2) I can derive P2 as 334.9 kN/m^2.
Or at least this is my thinking.
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was not, am not, accusing you of cheating. And I applaud your desire to learn. There are those (unscrupulous scalawags) who post to this forum trying to lure someone into doing their work for them; the standard response is, "Show me what you've tried."
There are experts in this forum that can/will help you--I'm happy to see Valerie post an example, this is one of his areas of expertise.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Really appreciate that and all the support you've given me over the years. I am genuinely just thirsty for knowledge.
I've looked at V's comment but am finding it really hard to follow without context.
Cheers,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@awibroe wrote:
Thanks Fred,
I've looked at V's comment but am finding it really hard to follow without context.
Cheers,
Andy.
See please http://www.springer.com/gp/book/9783319266732
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think I get the concept of using a solve block in this scenario. I could set limitations and then ask to find P2.
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Were your diagrams for PV and TS made in MathCaD?
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
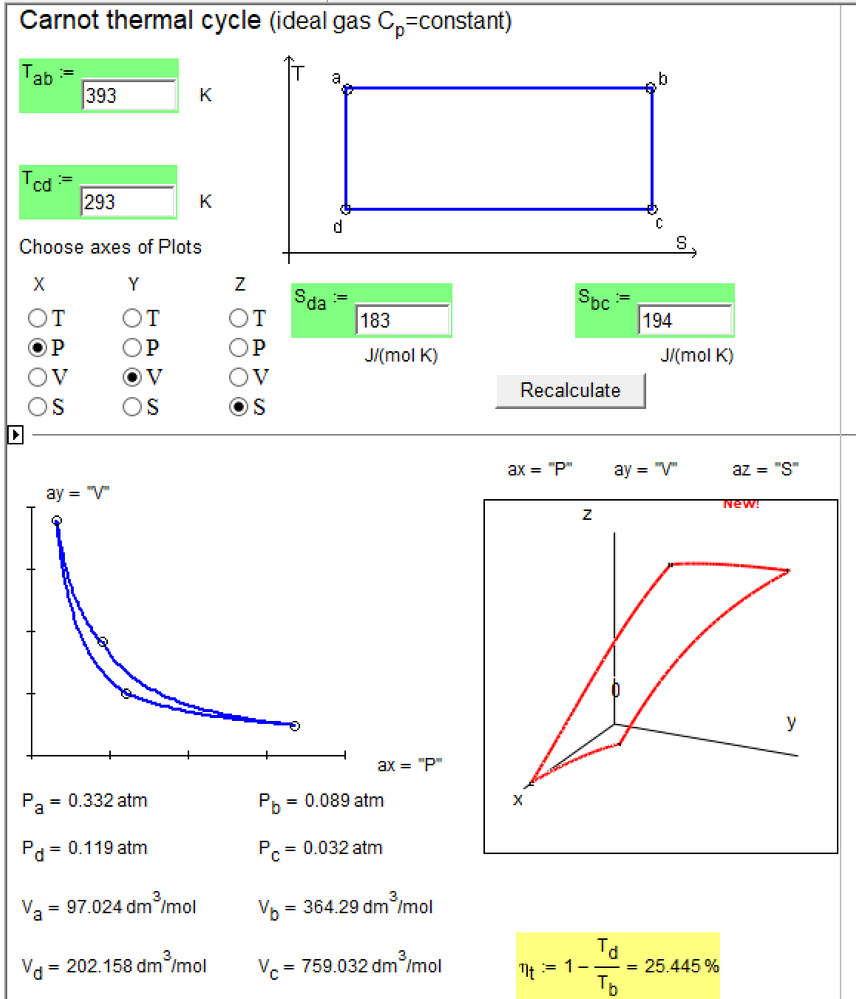
Try please this Mathcad Web sheet with Carno Cycle calculation with 2D and 3D diagrams
http://twt.mpei.ac.ru/MCS/Worksheets/Thermal/carno.xmcd
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree!
Looks like homework to me. Let's see the try.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
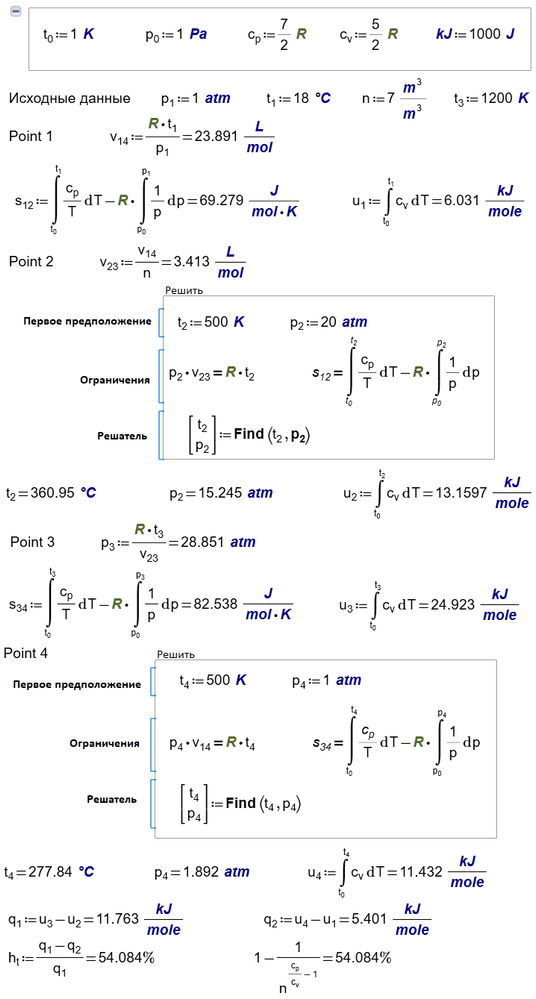
May be one example with Otto cycle help you