Very simple example attached. I was planning on looking at the friction losses and other parameters which effect the flow rate but ran out of time. 
Mike
Interesting pond you have there Mike. Not quite as interesting as your hose though!
The text in the *.pdf is class, nearly fell off my chair laughing .
Ok very poor example - I was doing my university work at the time, maybe shouldn't have bothered. The pond was already in the garden when I moved in and it keeps several large Koi Carp. The depth is closer to a meter thinking about it and the hose is more like 20mm .
You could have looked at friction losses due to imperfections and length of pipe........ Come on!!!!!!!
Oh, by the way......We only get about 2 days of sunshine a year here, so I wouldn't be filling the pond on that rare occurrence, bur I would have a beer in my hand.
Mike
That formula does take that into account, but only as long the flow is laminar. Then the friction factor is just 64/Re, where Re is the Reynolds number (i.e. you don't actually need to worry about the size of the imperfections).
Fair enough. Have a look below - an extract from one of our calculations.
We take the roughness of the pipe/hose material into consideration in our calculations, which I agree, for a garden hose could be ignored.
Mike
Well, this is something you know much more about than I do. I got the equations from here:
http://www.efunda.com/formulae/fluids/calc_pipe_friction.cfm
which says that as long as the flow is laminar the friction factor is simply 64/Re. If you simplify their equations using that assumption you get the equations given here:
http://en.wikipedia.org/wiki/Poiseuille%27s_law
So that's what I used.
There is one thing that I don't understand though. For my pond change the water pressure to zero and the elevation change to 1.5m. This represents a real case: when I drain the pond by siphoning over a retaining wall. It says it will take almost 90 hours to drain it, but I know that is not correct because a number of years ago I did it. It took a long time, but not that long! I am going to have to do it again this spring too, because the sludge has built up in the bottom to an unacceptable level 
Yes, I saw that equation, but I discarded it. The reason is that it's derived from Bernoulli's equation, which does not take into account the friction in the pipe. You have a 1.5m head of water giving a linear velocity of 5 m/s. That is a real jet of water! there is no way the water comes out of the hosepipe that fast. Your siphon would empty my pond in under 15 minutes. It didn't take 90 hours to empty, but it took a lot of hours, not 15 minutes!
Actually, since the viscosity and hose dimensions do not affect your calculations, if I filled my pond with treacle and used a 500ft hose to empty it, I would have a jet of treacle coming out of the end of the hose at 5 m/s 
Richard Jackson wrote:
Yes, I saw that equation, but I discarded it. The reason is that it's derived from Bernoulli's equation, which does not take into account the friction in the pipe. You have a 1.5m head of water giving a linear velocity of 5 m/s. That is a real jet of water! there is no way the water comes out of the hosepipe that fast. Your siphon would empty my pond in under 15 minutes. It didn't take 90 hours to empty, but it took a lot of hours, not 15 minutes!
Actually, since the viscosity and hose dimensions do not affect your calculations, if I filled my pond with treacle and used a 500ft hose to empty it, I would have a jet of treacle coming out of the end of the hose at 5 m/s
You're right. (Sorry it took so long to get back; work keeps getting in the way!)
But this is the right equation, we just need to add in the friction term. And the friction term is where length of the hose, diameter of the hose, and viscosity of the treacle get jammed in. The attached file is different (with the same name.)
You're right. (Sorry it took so long to get back; work keeps getting in the way!)
I know that feeling, although in my case this has been bugging me enough that it has been getting in the way of work!
But this is the right equation, we just need to add in the friction term. And the friction term is where length of the hose, diameter of the hose, and viscosity of the treacle get jammed in. The attached file is different (with the same name.)
Yes, I see. Thanks. But with the friction factor taken into account, If everything is correct we should get the same answers, because all the equations are derived from the Bernoulli equation. The answers are different because both our worksheets have problems! I think I have it figured out now though (famous last words!).
You calculate the velocity, and then calculate the friction factor. Then the you calculate a new velocity. The problem is, the friction factor you calculated is then not correct. You could iterate everything I guess, but it's not necessary (see the attached worksheet). As an aside, why do you have the base length set equal to 1 inch? This effectively sets 1in=1m, and really screws up the units handling. If I evaluate your surface roughness I get 0.85mm, which is a pretty rough hose!
Your worksheet did make me realize what was wrong in mine. I had the viscosity of water too high by a factor of 1000. Oops! Not quite treacle, but not water either! When I fix that the flow is not laminar, so then I needed to fix everything else too, using the correct friction factor. I think the attached worksheet is now correct. The numbers all look more reasonable now. It takes about an hour to drain the pond. It actually took longer than that, but this does not take into account restrictions in the pipe, or the fact that hose inlet kept clogging up! I'm a bit surprised I can fill my pond so quickly, but if I remember then I'm going to time everything this spring to check theory against experiment
Well, I finally found time to look at this again. Work is so inconvenient. It gets in the way of everything!
That's why the second solve block--let Mathcad find the velocity that fits the flow and the friction factor.
I'm not sure quite how I missed what you were doing there 
I've tried once more, using the values from your sheet. (For reasons I can't fathom your sheet will not compute in my version 11, so I can't see your answers.)
That is because of the temperature units. I have duplicated the new temperature conversion functions in the worksheet, so it now works in MC11.
If I put in exactly the same values for the viscosity, density and roughness then I can get your worksheet to give the same answer as mine if I make a couple of changes. One change is that the Reynolds number is a function of pipe diameter, so that needs to be carried though into the second solve block (otherwise it's always calculated for 20mm). The second change is that I removed the "1+" from your expression in the second solve block. Then the numbers match mine exactly. I believe mine is correct, for the reasons I mentioned earlier: if I take the simple case of laminar flow my derivation (which does not involve a "1+", just a multiplication) results in the Hagen-Poiseuille equation given here:
http://en.wikipedia.org/wiki/Poiseuille%27s_law
The draining problem is a differential equation--the driving head decreases as the level in the pond drops. I makefilling about 11 minutes, draining about 200 minutes.)
Yes, that is a very good point. The pond depth is significant relative to the siphon height, so this can't just be ignored. Draining is about 65 minutes though, not 200, because you are looking at how long it takes for the height to fall to Delta-z, whereas it only needs to fall to the depth of the pond (-2.5ft). I'm a little surprised this doesn't actually make a bigger difference. To get Odesolve to work after the changes mentioned above I had to cut the solution end point back a bit. I reduced the number of steps too, because I don't have enough patience! In my sheet I did use 1000 steps, because odesolve does not call a function based on nested solve blocks, so it calculates much faster.
I have attached two worksheets: a revised version of your sheet, and a revised version of mine.
This horse is gasping!
That means it's not quite dead yet. Get up horse!
Your logic seems sound to me, but then there's something I don't understand. See the attached.
I notice that the derivation of the Hagen-Poiseuille equation on Wikipedia involves a Taylor expansion, and then higher order terms are dropped. If the original equation on the website is not correct, which your derivation certainly indicates, perhaps that's why my derivation can get from that to the Hagen-Poiseuille equation. Seems like quite a coincidence, but it might be the reason.
Basically.
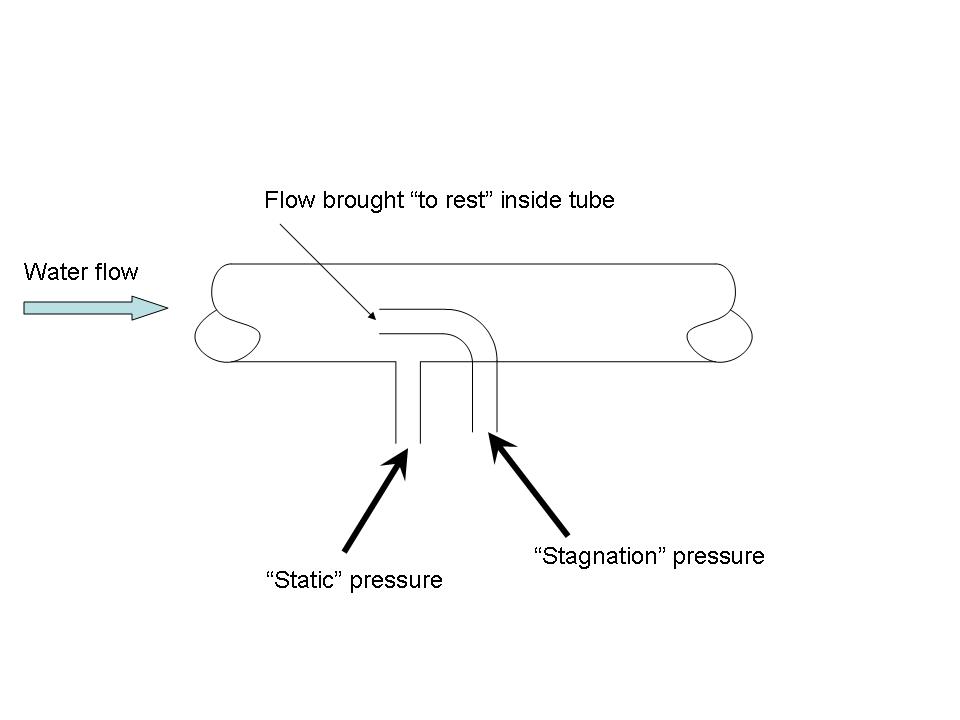
If I calculate the dynamic pressure (rho * V_fill^2 /2) at the spigot on the side of your house, I get about 4.3 psi. This is the difference between the pressure in the pipe with the spigot closed (the stagnation pressure) and the "static" pressure in the hose at the spigot with the spigot open and filling the pond.
Both the water in the house and the water in the pond have a "stagnation" pressure--that's the total amount of energy that can be used to push the water through the hose, some going to friction losses and some being converted to kinetic energy in the flowing water (AKA dynamic pressure.)
Total ("stagnation" or "pitot") pressure is always the sum of the static pressure and the dynamic pressure. Friction losses (extracting non-recoverable energy from the flow) subtract from the total pressure (and, therefore, from the static pressure too.) So we're both right.
So the stagnation pressure includes the pressure due to height? Then the house water pressure is not the stagnation pressure. Or the static pressure. It's something else, for which I don't have a term, that is equal to the stagnation pressure minus the pressure due to height.
Richard Jackson wrote:
So the stagnation pressure includes the pressure due to height? Then the house water pressure is not the stagnation pressure. Or the static pressure. It's something else, for which I don't have a term, that is equal to the stagnation pressure minus the pressure due to height.
Let us measure ALL pressures relative to the atmospheric pressure at the discharge end of the hose (P_atm).
Then:
The static pressure at the end of the hose is zero. (The pressure water at the end of the hose is the same pressure as the air it's discharging into.
P.static_end = P_atm, but we're measuring relative to that, so P.static_end - P_atm = 0 psig.
The dynamic pressure in the hose is rho/2 x V^2, and it's constant anywhere in the hose. (The hose is constant area, so the water coming out is at the same speed as the water going in and the density is the same (water is virtualy incompressible at these pressures.)
So the stagnation pressure at the end of the hose is: P_o_end = P.static_end + rho/2 x V^2 psi gage (= P.static_end + rho/2 x V^2 +P_atm absolute.) But we said above that P.static end = 0, so P_o_end = rho/2 x V^2 psi gage.
At the spigot (at the house), the dynamic pressure is the same. The stagnation pressure is:
P_o_end +rho x g x Z +rho/2 x V^2 x friction+P_static_in===the stagnation pressure at the discharge plus what was lost to friction plus what we gain from the elevation change plus the static pressure in the hose. Substituting for P_o_end, we get P_o_in = rho x g x Z +(P_o_end = rho/2 x V^2) +rho/2 x V^2 x friction + P_static_in
or P_o_in = rho x g x Z + rho/2 x V^2 x (1+friction) + P_static_in
