Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
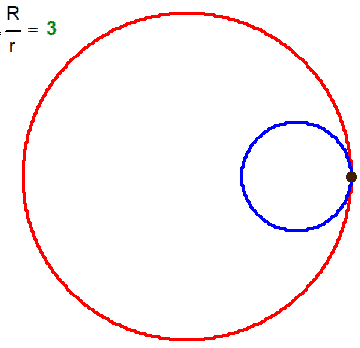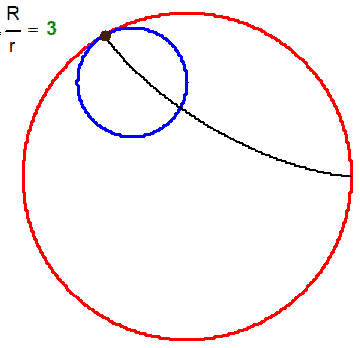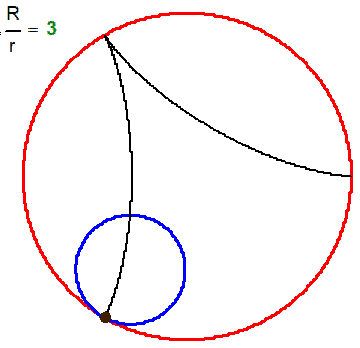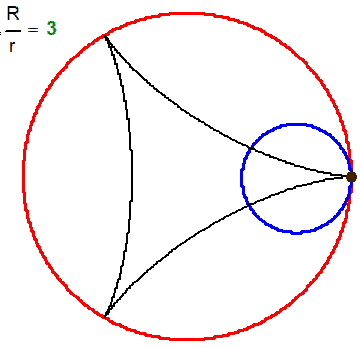
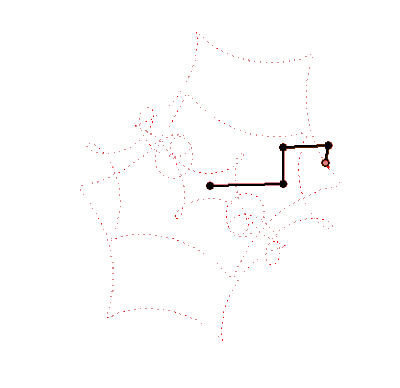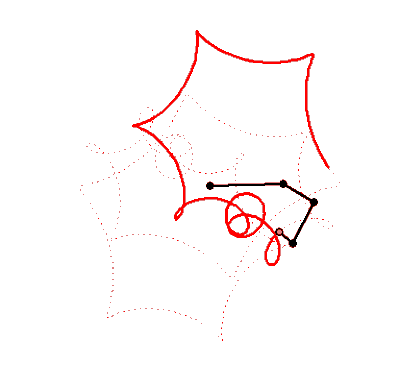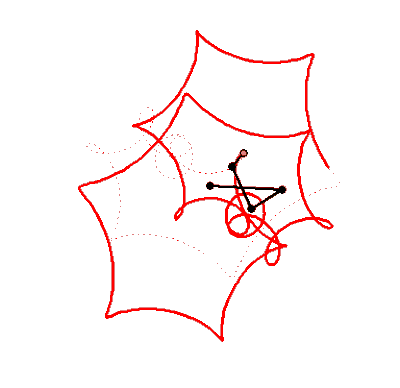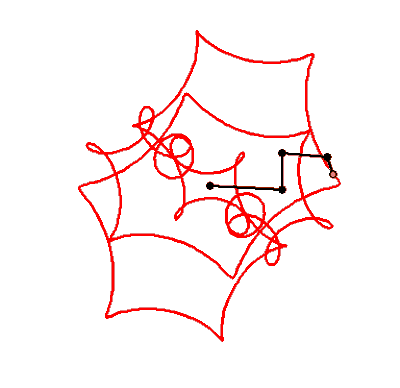
What name has this closed curve?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
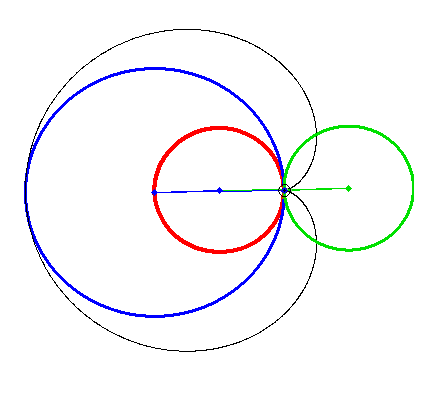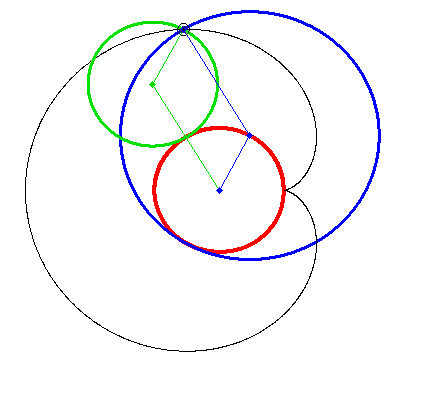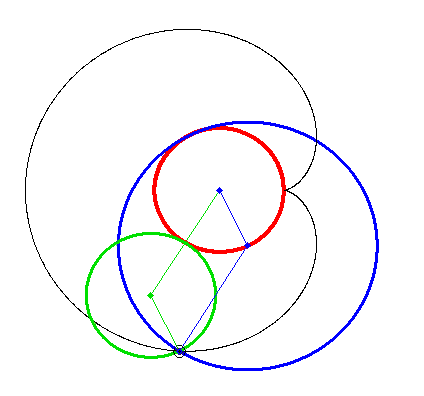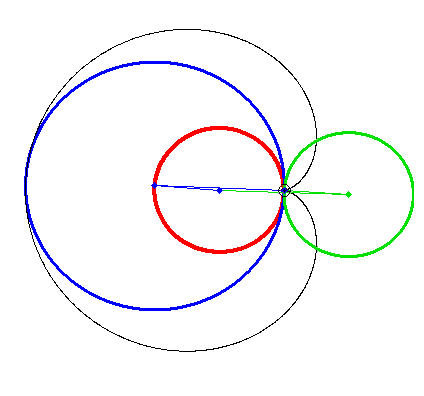
What name has this closed curve?
It is a deltoid (one hypecycloid)
It is a cardioid (one epicycloid) - one alternative method of plotting
What is it?
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not every curve has a unique own name - there are too many of them 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
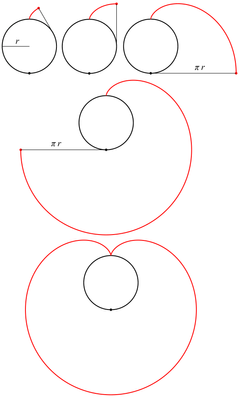
Well, they can be made with the child's toy known as the Spirograph. And the wikipedia entry for that calls them roulette curves.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the cardioid is not one epicycloid but one hypocycloid too!
Or we have not two but three kindd of of curves - epicycloids, hypocycloids and ??? (see above)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Names of curves often are chosen after the way the are created. These "rolling curves" (German. Rollkurven) often also are created by so called planetary motion (German: Planetenbewegung).
Epizykloids are also called Hypercycloids or (German: Aufradlinien) and Hypocycloid are (German: Inradlinien).
Most Authors distinguish between cycloids and trochoids, but some call them both cycloids. The latter is wrong in my opinion as a cycloid is a special trochoide, but not the other way round.
So, as usual names are not standardized and always matter of confusion.
Every trochoide (no matter if epi.. or hypo... and no matter if cycloide or not) can be created in two ways by rolling two circles.
In the case of the epicycloide, the second way to generate it usually is also called an epicycloid, but sometimes its called a pericycloid
I think it makes sense to use a third name (pericycloide) as the motion for the pericycloide has more in common with that of a hypocycloide than with that of an epicycloide IMHO.
If the moving point is not on the circumference of the rolling circle, the curve is of course called a peritrochoide. An example for a peritrochoide is the hull of a Wankel-motor -> http://www.animatedengines.com/wankel.html
BTW, in the link above you also see a refernce to "507 Mechanical Movements". A lot of them are not (yet) animated (some quite simple, some more complex). Maybe a stimulus for you and/or your students.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I never cease to wonder and marvel at how these books were written without Maple, Mathematica, Mathcad etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Long ago I saw a textbook on drafting (how to make engineering drawings for manufacture.) There were chapters on the techniques for developing gear tooth forms, and how to develop these curves.
Just as Mathcad, Maple, etc. have made drawing the curves simple, the current modeling programs have made drafting on paper with squares, triangles, and compasses obsolete.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, many techniques, I spent a lot of time mastering, are kind of obsolete now. Nevertheless, I don't want to miss this knowledge. When we learned how to draw a square, we learned so much more than just making that figure.
And if I look at old textbooks and their illustrations and compare them with the ones in newer books - no comparison! There sure are less pictures in older books because of the effort involved in making them, but this also resulted in authors very carefully selecting what to show. Thats what I sometimes miss in newer publication where there is sometimes an inflation of often rather insignificant illustrations.
And when I look at old technical illustrations - how much more beautiful they are!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is your animation with a different timing, showing the connex
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!
I wanted to create a similar animation, but I thought that Werner could not resist and create it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There sure are enough other animations left for you 😉
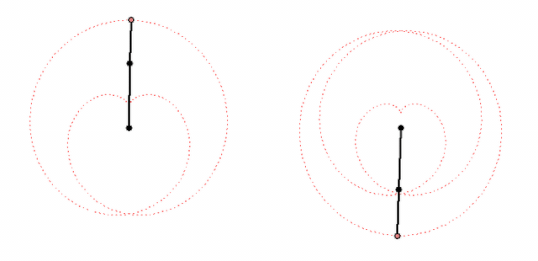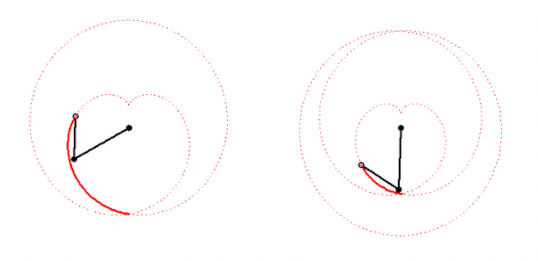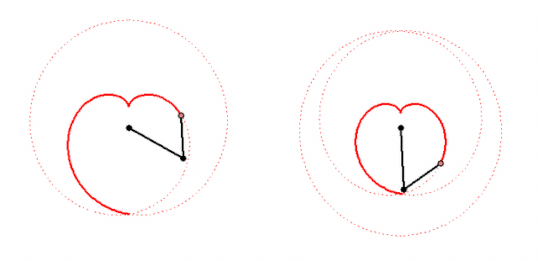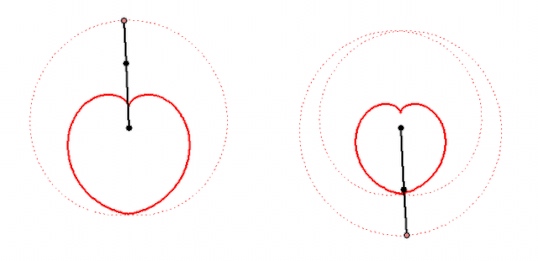
Every of these curves can be created by letting a point rotate around another point which in turn circles around a fix center. The points rotate with constant, but not necessarily the same speed.
My animations shows two ways to create a cardiode that way.
Of course you can cascade this procedure, letting a third point circle around the last one and so on. That way you cam to "Radlinien" of higher order. A pioneer in the theory of these curves was Prof. Wunderlich. His fundamental paper can be found here: http://sodwana.uni-ak.ac.at/geom/mitarbeiter/wallner/wunderlich/pdf/17.pdf
Enouh material for many many animations 😄
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My animation is more... real: three cyrcles have one common point!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, whatever "real" may mean here 😉
Using the parallelogram shown in my animation it would be possible to create a "real" mechanism moving oth wheels with different speed, too.
Here a quick implementation of the "Radlinien" of higher order. Quite easy to do using complex numbers.
I leave it up to you finding multiple ways to create the same curve or finding the radii of the circles (gears) to create those movements.
MC15 sheet attached - can be used for curves of arbitrary order, but I have not yet found a way to automatically calculate t.2, the minimum number of cycles for t to make a fulll "revolution". It has to determined and set manually according to the speed values in vector v.
Animation is created with 720 frames at 36 frames per seconds.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I love looking at this kind of animation. It's like our life - at first everything went according to the laws, and then there was an epidemic and everything went wrong!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
I love looking at this kind of animation. It's like our life - at first everything went according to the laws, and then there was an epidemic and everything went wrong!
Life never goes according to laws. (Physical) Laws always can only be an approximation.
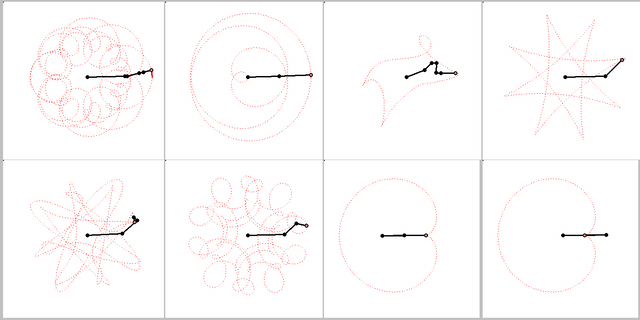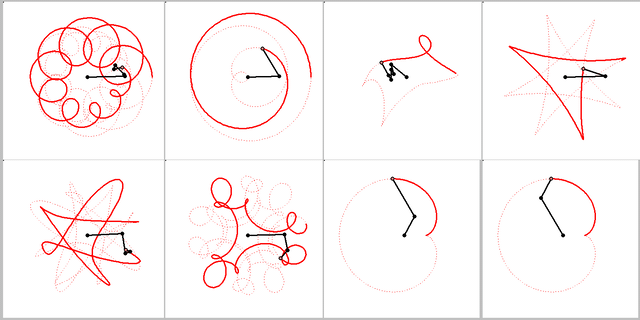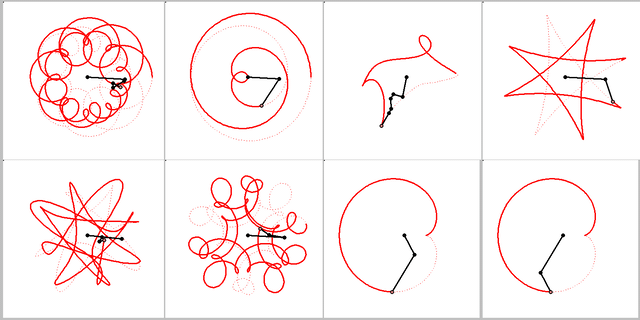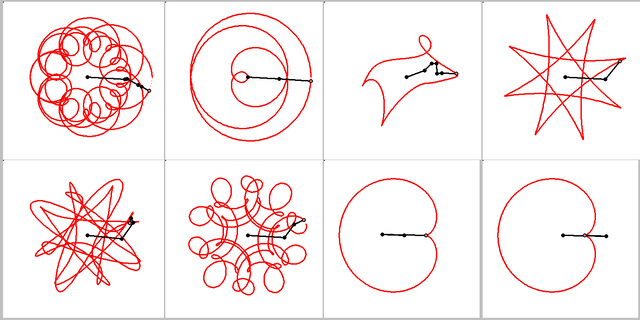
Guess your animation has nothing to do with the topic you had chosen for this thread. It belongs to a different, older thread, as far as I remember. After all the topic here was about a curve created by rolling a circle on another. The curves below can also be created that way (using multiple gears, of course). You already know how to do it for the last two 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
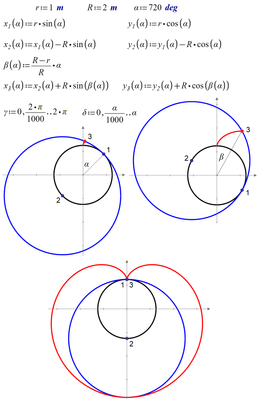
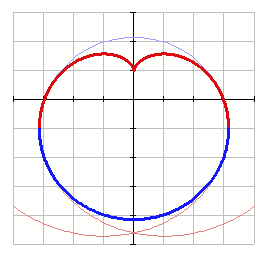
But why do you think that this orientation is "correct" ???
EDIT: Ah, I think I know - it's because of the supposedly heart-shaped appearance of the curve, right?
I've actually never found the curve to be reminiscent of a heart. Anyway, there are better ways to generate a heart-shaped curve.
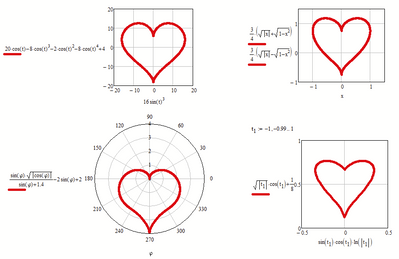
Here are some examples I collected a while ago:
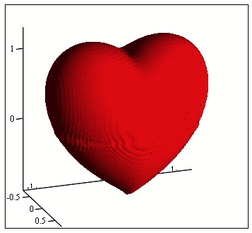
Or even in 3D (thanks to Viacheslav N. Mezentsev's "implicitplot3D()"):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is the cardioid with correct position and correct form
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
It is the cardioid with correct position and correct form
I am still not sure what exactly you mean??
Are you really just referring to the heart-shape of some part of the curve??
Anyway, I'll add it to my collection 😉
What you show is not called a cardioid 😞
The naming of the curves after real things was very free and creative. Just think of a nephroid and a real kidney:
Compare this nephroid
with https://de.wikipedia.org/wiki/Datei:Lammnieren.jpg
I think a cardioid looks more like a kidney than a nephroid 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the real heart - the cardioid. And what was painted before looks like not a heart, but another place in the human body!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
This is the real heart - the cardioid.
OK, so it looks that the whole discussion about "correctness" was just about the shape!?
And what was painted before looks like not a heart, but another place in the human body!
I guess you won't be able to convince the professional world to suddenly rename something internationally known as "cardioid" to something like "buttoid" (or would you prefer "bunoid"?). 😄
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery, Werner,
Thank you both for this beautiful thread, and Werner, for the paper - uh, if only I could read German! But the math should be universal!
Proud user of Mathcad since MS-DOS days.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
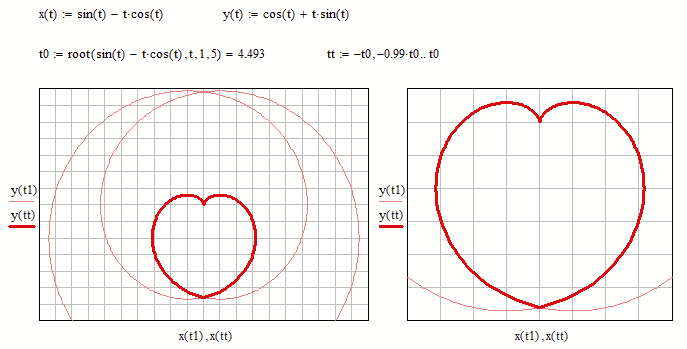
One more cardioid
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
One more cardioid
No, sorry - its not a cardioid even though on first sight it may look like a cardiode.
But its just a heart-shaped(?) curve composed of part of a circular involute (=evolute) and a semicircle. But they blend into each other rather well as they match at the transition point in the first two derivatives (same point, same direction, same curvature).
If the goal is to create a heart-shaped curve, you could do it with just Hygen's circular involute alone - without the semicircle.
P.S.: It seems like we're working towards Valentine's Day very early 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
" It seems like we're working towards Valentine's Day very early"
Everybody needs a little love!
Anything that gets us out of 2020! 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I forgot to write that in my youth I worked as a milling cutter! I made gear wheels on the machine!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
About non classical cardioid by non classical method, according to Wiki, a cardioid could be also obtained by fractals geometry, by the so called Mandelbrot set !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And about planetary motions and the spirograph I found this on Wiki:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
About the name of trigonometric function, why sin(x) is called sinus?
According to the Italian Wiki this is due to an “error of translation" by Gherardo da Cremona (1114-1187, https://en.wikipedia.org/wiki/Gerard_of_Cremona) while translating from arabic to Latin the Algebra of al-Khwārizmī, The arabic word "jiba" was originally referring to the sanskrit word for chord not bay (sinus in lat.).
According the English Wiki the same error was made by Robert of Chester https://en.wikipedia.org/wiki/Robert_of_Chester