Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
atan( ) , ln( ) and Find( ) _ (2)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
atan( ) , ln( ) and Find( ) _ (2)
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Where is your problem? You simply let Mathcad do its job without any tricks at all:
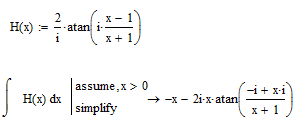
A better way with a little thinking over the problem beforehand may be this:
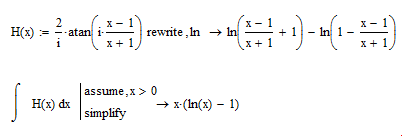
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not sure what you are looking for. The symbolic solution for X is just tan(LHS). Or are tthe x on the LHS and the X on the RHS supposed to be the same?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmmm. Actually, Given...Find gives an interesting answer. What is "ImageSet"?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your time and help, Richard. And I have a query :
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As in some previous posts you don't account for the ambiguity of the atan() "function" (its just a relation, not a function). Likewise the ln(complex) is not unique!
atan(tan(x)) = x is true only if you limit x to the range -90° to +90° and Mathcad is aware of this:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
... What is "ImageSet"? ...
Maybe this: http://sst.unisim.edu.sg/apps/maths/Interactive%20Maths/Dynamic/Imagex%5E2.htm
Image Set of y = x^2
The image set of the function f(x) = x^2 is shown when its domain is the closed interval [a, b] (you can drag and change the lower and upper domain limits a and b). Note how the image set is given by [f(min), f(max)] (for a < b within the applet) with respect to the domain [a, b]. You can also click to animate the lower domain limit a to move towards the upper domain limit b. Note how the corresponding image set changes.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
Hmmm. Actually, Given...Find gives an interesting answer. What is "ImageSet"?
http://www.mathworks.de/de/help/symbolic/mupad_ref/dom-imageset.html
You get a similar result (but w/o ImageSet) if you use solve with the modifier "fully"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see. Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And need help with the related query :
Thanks in advance for your time and help.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You probably expect X=i, but again you have to consider the ambiguity of the used function(s):

Different results for X depending on the value of x!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And I have another related query :
Thanks in advance for your time and help.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may either evaluate the integral numerically or symbolically with the modifier "float".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your integral can be written as
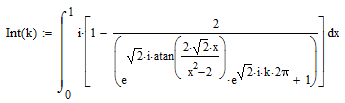
with k being any integer,
So again you are running into ambiguity. You get different result for different values of k and for some values of k the integral does not converge at all (k=4, k=9, according to Mathcad). So ir seems you can't expect a closed solution.
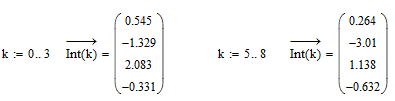
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for your time and help, Werner.
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And I have another related question :
Thanks in advance for your time and help.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You experience the effect of numerical inaccuracy combined with ambiguity of "functions" (again!). E.g. Mathcad choses pi for the atan(..) for some values of x, giving the total result -2pi. Mathcads numerics add the very small imaginary part (which should be zero) and so that point isn't plotted. This happens quite often and so you see the holes in your graph. Reformulating the function definition as I had shown in another thread with the f1b() may help, but mustn't necessary. If you want to be on the safe side, define f2(x):=0. 😉
Can you tell us what you want to achieve with all this? You seem to know that used function are equivalent and the difference should simplify to zero - at least given some implicit assumptions about the domain of the involved variables and functions which Mathcad doesn't make. So whats the goal of all these attempts?

I am not sure why MC can write atan() as ln() but not the other way round. Both functions show ambiguity if applied to complex arguments (so strictly spoken they can't be called function therefore). Maybe is has to do with the fact that ln() is unique in the domain real and so Mathcad refuses to rewrite it with an ambiguous atan(). Maybe is just one of the many disabilities of MCs symbolics. Maybe it even can be done using the right combination and order of symbolic assumptons and keywords, Maybe ....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for the following, Werner ![]() :
:
Werner Exinger wrote:
You experience the effect of numerical inaccuracy combined with ambiguity of "functions" (again!). E.g. Mathcad choses pi for the atan(..) for some values of x, giving the total result -2pi. Mathcads numerics add the very small imaginary part (which should be zero) and so that point isn't plotted. This happens quite often and so you see the holes in your graph. Reformulating the function definition as I had shown in another thread with the f1b() may help, ...
I am not sure why MC can write atan() as ln() but not the other way round. Both functions show ambiguity if applied to complex arguments (so strictly spoken they can't be called function therefore). Maybe is has to do with the fact that ln() is unique in the domain real and so Mathcad refuses to rewrite it with an ambiguous atan(). Maybe is just one of the many disabilities of MCs symbolics. Maybe it even can be done using the right combination and order of symbolic assumptons and keywords, Maybe ....
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And another related question :
Thanks in advance for your time and help.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Where is your problem? You simply let Mathcad do its job without any tricks at all:
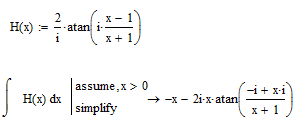
A better way with a little thinking over the problem beforehand may be this:
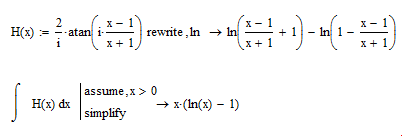
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have Mathad 14. And :
The screen has showed :
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The screenshots were made on machine way more feeble than yours, but using Mathcad 15 M030.
You just have to wait for the last region to evaluate - it takes quite some time, a minute or two if the region is evaluated the first time.



