Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
curve fitting
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
curve fitting
hi
This mays be a little trivial and repetitive but i havent found a manual. a tutorial or something that shows mathcad functions which do this. i found somes examples in here and i tried to used them with my data and they didnt work.
i got this data that represents a curve and i want to find a function, maybe a Lagrange interpolating polynomials that fits this data. i have attached a sheet with the data. if some one could help me.
Thank you in advance
- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
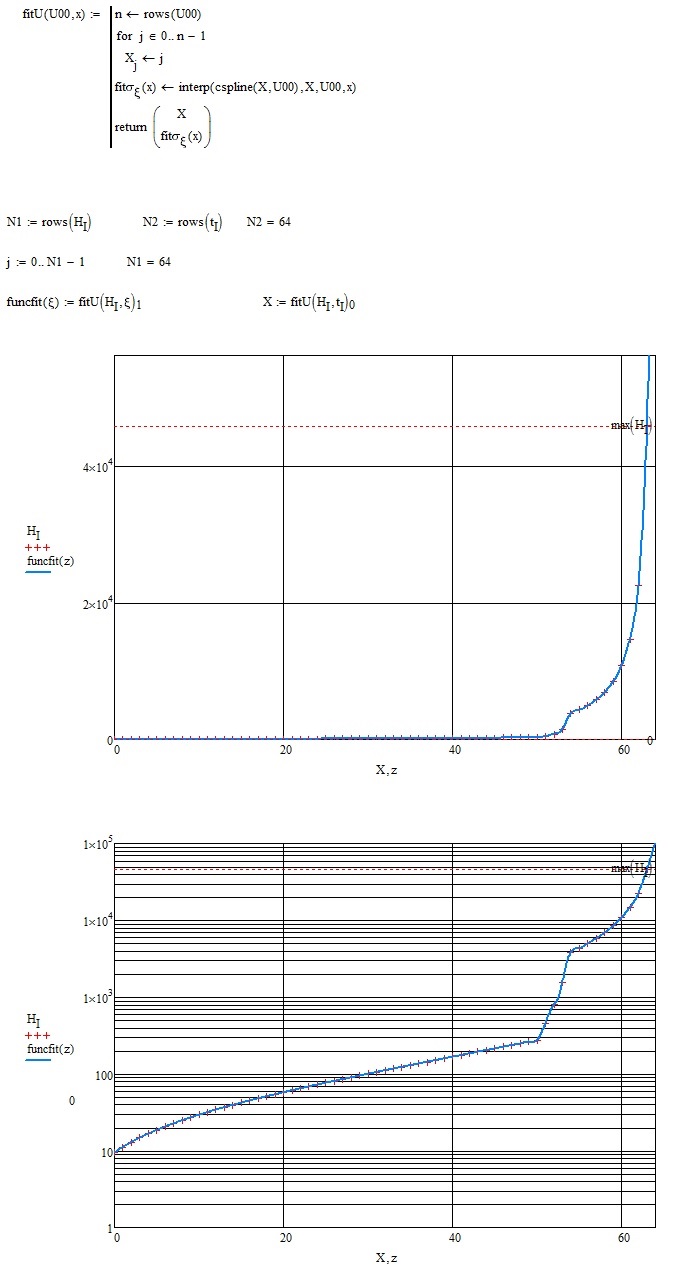
Hi Wander
this is my solution:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I cheated, used CurveExpert to sort thru functions.
Taking the log of H yielded a fairly good fit over most of the range; the very high end has a problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you take the log of the H.I values then a polynomial gives a reasonable fit, but a rational polynomial gives a better fit, with fewer terms.
Or you could use spline interpolation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
wander perez sena wrote:
i found somes examples in here and i tried to used them with my data and they didnt work.
You would have to be more specific if you'd like to receive some help on this and provide the examples and what you did which did not work.
i got this data that represents a curve and i want to find a function,
Do you need an analytic function or would a piecewise interpolation would do the job as well? Or are you in need for a regression function (of which type?)?
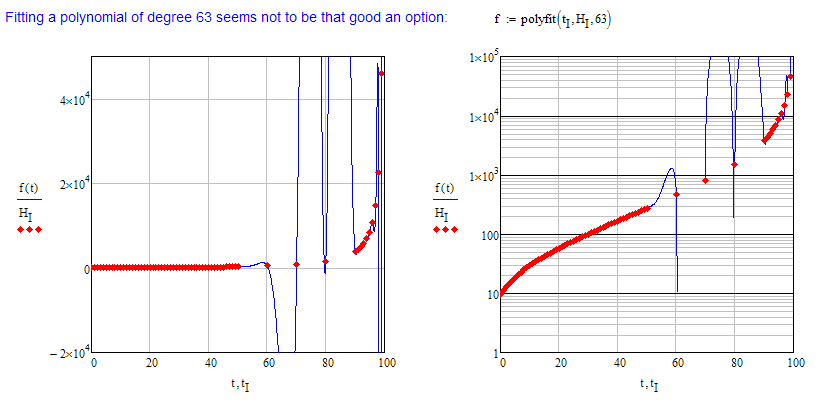
maybe a Lagrange interpolating polynomials that fits this data
Hmm, this would be a polynomial of order 63 and sure suffers from some bad oscillations. Wouldn't recommend using it:
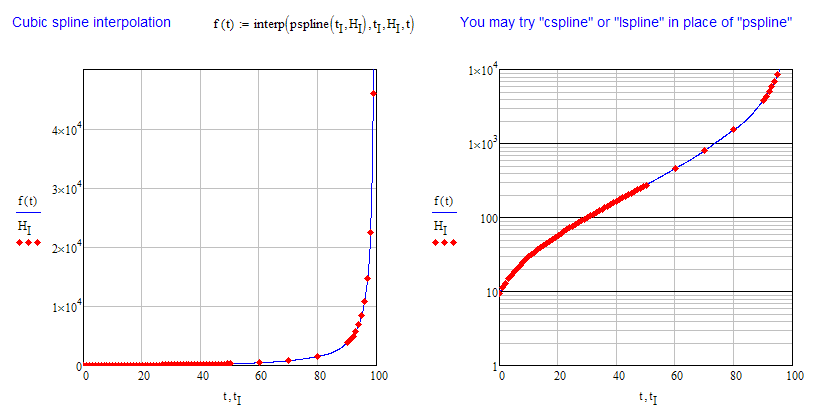
If interpolation is all you are asking for, you basically have the choice between simple linear interpolation (see attached file) or cubic splines:
If you are in need for an analytic function you would resort to an approximation by regression. Playing around and trying various function types, I, too, found, that a rational polynomial gives the best fit so far. But Richards approach of fitting the log data with a rational of higher degrees polynomials gives you an even better fit.
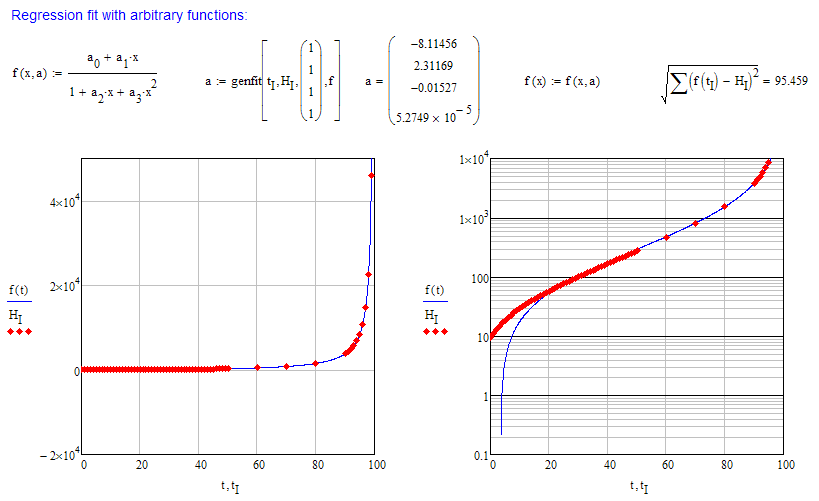
Regards
Werner





