Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
generate a specific combinatorial sum symbolically
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
generate a specific combinatorial sum symbolically
Collabs,
I need help with generating a specific combinatorial sum for the symbolic processor (Mcad 11).
See attachment.
Thanks for your time
Luc
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the attached shows a simple function that does what you want.
stv
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc
Haven't really spent much time using symbolic's, but think I have solved for Equation 2.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, Luc ! ... You are liquefying my brain .
I have recognized 3 quicly enough .
But if it can be completed, then numerical is just enough.
What all that does represent ? Has it got something to
do with the "Chemical pseudoinverse" ?
I think Stuart & Richard would be good in there [Mike too].
Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Jean,
To (partly) satisfy your curiosity:
the expression is part of the denominator of an expression that describes outputs of a specfic n-channel amplifier.
In there each Ai is a more complicated expression by itself.
Mathcad (11) is capable of solving my entire n-channel amplifier symbolically, sometimes up to n=4, after which I can evaluate solutions numerically, for n=4 and higher (haven't tried to find the limit yet).
I want to describe the (full) solution in a way that enables to understand it's structure. So I need a compact description of that specific sum of n summations.
That requires I need to "simplify" and you know how good CAS systems are at simplifying.... although I learned a few new tricks in Mathcad along the way.
Thanks,
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc Meekes wrote:
Jean,
To (partly) satisfy your curiosity:
the expression is part of the denominator of an expression that describes outputs of a specfic n-channel amplifier.
In there each Ai is a more complicated expression by itself.
Mathcad (11) is capable of solving my entire n-channel amplifier symbolically, sometimes up to n=4, after which I can evaluate solutions numerically, for n=4 and higher (haven't tried to find the limit yet).
I want to describe the (full) solution in a way that enables to understand it's structure. So I need a compact description of that specific sum of n summations.
That requires I need to "simplify" and you know how good CAS systems are at simplifying.... although I learned a few new tricks in Mathcad along the way.
Thanks,
Luc
Thanks Luc, for the explanation.
Though I don't understand the logic in such complicated construct, but applied it quick. That would represent a coding of some sort [just a comment to maintain my brain in gear]. Your last part is the permutation, that works symbolically but can't be extracted . We need a brain storm from collabs in there ! Another way to get the permutations is the lexico construct or from tables [Neil Sloane]. But you have to make sure that all the components are really as they reveal up until your expression [4]. If all those components are true, what's left is the symbolic construct of the permutations, for instance the 6 permutations of [a,b,c] = [a,b,c], [a,c,b], [c,a,b], [c,b,a],[b,a,c], [b,c,a] ... most gorgeous would be an "n permute". The rot(v,n) does it but can't be extraced symbolically for a literal module to apply. I'm sure any reader will be interested as already tuned to the challenge. BTW, the centroid member works for any length but it sems you ignore the last term.
Cheers Luc, Jean
>>>>>>>>>>>>>>>>>
The spell check does not in there , Why ? Don't know.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jean Giraud wrote:
>>>>>>>>>>>>>>>>>
The spell check does not in there , Why ? Don't know.
The spell check also can't understand two words joined without a gap. It just makes a suggestion of the first word, doesn't offer a space as a suggestion - Unlike WORD.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
Solved equation 3 see attached. As Jean said one of the more experienced users should be able to show a simpler solution than mine. Hey, still works though.
Cheers
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luke.
No feedback on the sheets I provided!!
No good?
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike,
sorry, I hope I didn't offend you.
I've looked at them to see if I could generalize your particular solutions and saw no way (yet).
Regards,
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc Meekes wrote:
sorry, I hope I didn't offend you.
I've looked at them to see if I could generalize your particular solutions and saw no way (yet).
Regards,
Luc
Luc,
Not at all.
Gold star to Alan for solving.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Luc,
Finished but the last permutation, can't get it work symbolic otherwise than local and manual, i.e: can't be programmed. Will post tomorrow. Make sure the pattern is extensible , it's not obvious even with expansion 4.
Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
You will understand everything. You can really make it as you wish but for the last term, if you want it more developed, it will take a big bit more construct even for a permute as simple as [a,b,c]. .. But it would be possible. Was very interesting, I never thought the "Centroid" could be applied. In fact, it could do the all lot by itself whereas it is variable in length. Just a matter of adapting or revising the concept of the project [speaking to myself].
Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the attached shows a simple function that does what you want.
stv
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan,
Looks like you have crack it.
Can you explain how the fucntion still works when RED?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"Can you explain how the fucntion still works when RED?"
It's only the numerical solver that would need the a's to be pre-defined. The symbolic solver doesn't give a monkeys!
stv
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of course, cheers Alan.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Alan,
I suspected that it should be doable by a function, although I thought a recursive function would be needed (if you look at my attempt, you'll see why).
You showed that that isn't necessary.
I've checked your solutions against my stuff, and as far as I've gone the solution is correct.
Now my next task is to embed this function in my symbolic calculation sheet, and see if it works there.
Thanks!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Works fine here.
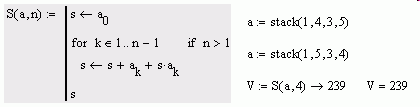
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
... not really "combinatorial"
independent of shuffling vector (a)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan Stevens wrote:
I think the attached shows a simple function that does what you want.
stv
Alan,
It does, though I missed in the first place. As is, it outputs a single value. I may have muffed the grouping in my first attempt.
Thanks, saved





