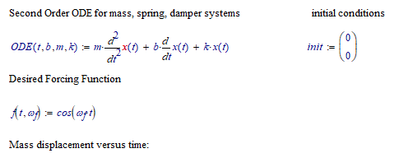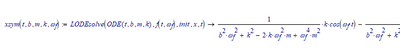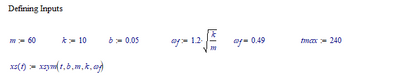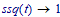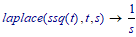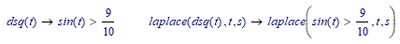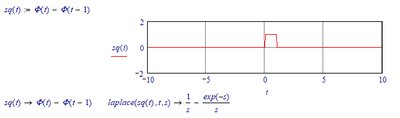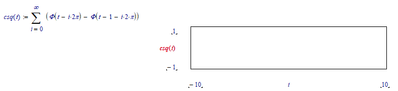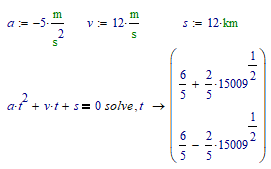- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
output of odesolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
output of odesolve
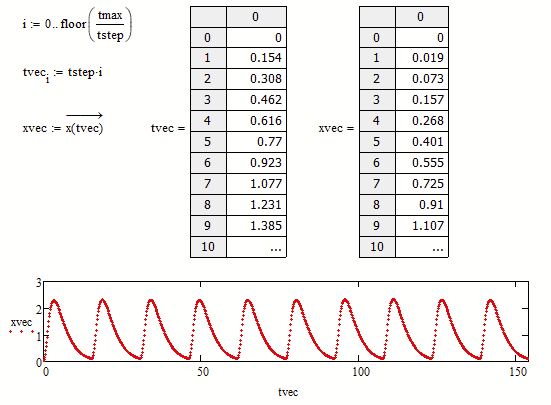
is there a way to convert the odesolve output to a matrix, so that the max and min can be found. apparently the odesolve output is a function. i attached a worksheet. i want to convert t and x to matrices.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@prop_design wrote:
is there a way to convert the odesolve output to a matrix, so that the max and min can be found. apparently the odesolve output is a function. i attached a worksheet. i want to convert t and x to matrices.
How about
Of course you could use any vector "tvec" as long as its elements are all in the range from 0 to tmax. You may simply replace tstep by any other value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@prop_design wrote:
is there a way to convert the odesolve output to a matrix, so that the max and min can be found. apparently the odesolve output is a function. i attached a worksheet. i want to convert t and x to matrices.
How about
Of course you could use any vector "tvec" as long as its elements are all in the range from 0 to tmax. You may simply replace tstep by any other value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks werner,
i had been trying to use vectorize but it wasn't working for me. i'll try again. i must have been missing something.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
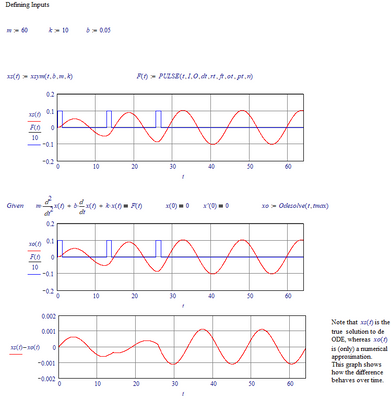
Before there was ODEsolve there were the line solvers, (Adams, rkfixed, Rkadapt, Bulstoer, and Radau).
rkfixed et al are still there, and the output is the matrix you're looking for.
ODEsolve automated one of the line solvers and fit a curve to the points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks fred,
i remember those days. i remember keeping up with the changes in the solvers. i don't recall the output differences though. i'm forgetting a lot. i actually like the odesolve output though. having it be a function makes some things a lot easier. but then you need to convert it, which had me stuck. thanks to werner for unsticking me. the state space output is in a matrix and it seems like the last column of the matrix is velocity. however, it doesn't match up with the velocity you get using the time and displacement output. so i'm still confused there. but all of my other questions were answered by forum users. so many thanks to all. i have the examples posted. i have been updating them a lot and updating the post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hi fred,
i did further work on the examples and found some interesting things that relate to what you mentioned. it may be better to use the older solvers. taking derivatives of the odesolve function output is very slow and causes some error to show up. also the derivatives are working badly. sometimes you have to take the second derivative of displacement because the first derivative of velocity won't solve. other times you have to do the opposite. it is much faster and less error to manually calculate velocity, kinetic energy, and acceleration manually from matrix output. also the reaction force calculations. i converted the state space matrix output to a function and took derivatives as another test. it displayed the same problems. so the issue is definitely with the derivatives and not the solvers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Electric circuit analysis of the same system.
- Tags:
- Prime 7.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hi,
this is interesting. is there any way you could provide something similar in a MC15 file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Mathcad 15 it can be done even better.
First let me refer you to: https://community.ptc.com/t5/PTC-Mathcad/Toolbox-Solving-Ordinary-Differential-Equations-symbolically/m-p/689336
From there you fetch LODEsolve.xmcd
Then you can use the file attached here. Note that the file is written in Mathcad 11, so with Mathcad 15 you may see the symbolic output differently formatted, which may require you to move regions, in order for them to be separated. Then you can enjoy.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks luc,
i'll take a look at this. much appreciated. i've been noticing some problems with all of the numerical solvers in MC15. There are random errors popping up in different spots depending on the solver. None of them seem capable. The errors are hard to spot visually, but i've started to get good at finding them. So it's now become important to look into the symbolic solution instead. unfortunately, that's something i have almost no experience with.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hi luc,
i've been looking over the various files you mentioned. i'm afraid i can't figure out how to call the solver. i attached a MC15 file, but i'm not sure if you can open it. I think you are using MC11. i attached a picture as well.
ideally, i'd like to use three different forcing functions. cosine wave, sine wave, and square wave. i'd like to be able to change the damping ratio and other parameters as well. to operate in different regions. i'm not sure if your solver cares which region you are in or not. so stuff like beats, resonance, under damped, over damped, critically damped.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Note that LODEsolve is a SYMBOLIC ONLY function, it does not evaluate numerically. But of course, as with any symobilic expression, you can assign its result to a function and evaluate that numerically. You almost did that in your MCAD15 file: xsym(t):=LODEsolve(ODE,f(t),init,x,t).
The one thing you forgot was the symbolic evaluation, so it should be:
xsym(t):=LODEsolve(ODE,f(t),init,x,t) ->
(That is, press [CTL >] at the en of the expression.)
1. How did the file operate in Mathcad 15, that I attached specific to your problem (The file LM_20210429...)?
2. The LODEsolve() function should function with the first two of your proposed f(t), not with the third.
The reason for that is that the symbolic processor cannot handle the mod() function. You'll have to create a square wave using the heaviside step function.
As for functional properties of the ODE (whether or not damped, critical or whatever): The LODEsolve() function does not care. It executes a pure mathematical operation (an automation of what ttokoro showed) that, if the ODE meets the requirements for it, and a solution can be found, will produce the solution. And if you work with a pure symbolic expression you get a pure symbolic mathematical function.
I've elaborated your example here:
gives:
Note that the expression runs out to the right for a couple of pages. In Mathcad 15 it may look differently, due to another symbolic processor.
Now we can use the (result) function xsym:
and plot the results over time
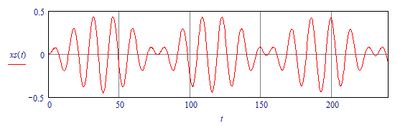
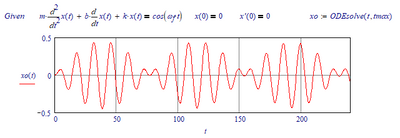
Note that the Mathcad built-in odesolve function produces apparently the same result.
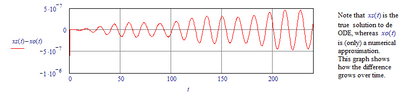
But it's not EXACTLY the same, if I subtract the ODEsolve result from the LODEsolve result:
With the very same xsym() function you can now experiment with different values of b, m, k and omega.f.
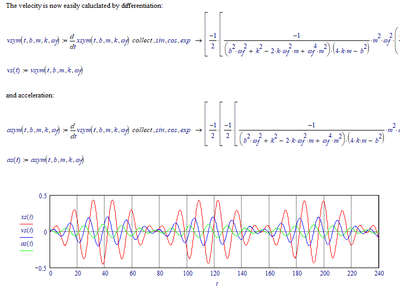
And you can easily calculate differentials:
The Mathcad file is attached.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks luc,
the example you sent worked in mc15. i just didn't fully understand how to use it. the attachment you just sent also works. i only had to add a simplify command to the acceleration result, to remove a warning it was showing. i'll try to figure out how to do a square wave. not sure if i will be able to or not.
yeah, having worked with the numerical solvers for the last few days, i see they are having unexplainable problems. odesolve looks to be mostly boundary issues. state space is weirder. it's ok at the boundaries but inboard seems to randomly go haywire. so that's what got me interested in trying a symbolic solution. some examples i have seen the growing error that you showed. it seems to depend on inputs. the attachment you just sent might have different inputs than your pic. the error isn't growing in mc15 but oscillating. not a big deal, i have seen error like in your picture before.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The warning on the acceleration function probably deals with it 'being too large to display'. That should be no problem, you still can work with it. Once you start to work with square waves that are symbolically acceptable you will see that warning more often. Note that you can still work with the (symbolic) result, even if it cannot be displayed.
Regarding square waves: See if this helps for you. It's not finished, some things don't work to my satisfaction in Mathcad 11. But they may work in Mathcad 15, and be of use to you.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks a lot. i got the cosine and sine waves working. your example helped me see what i was doing wrong with calling your function. i have to run errands for awhile. but i'll check out the square wave when i get back.
edit; yes, that is what the warning was.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hi luc,
this was very helpful. i have been messing with it, so that i can use it in my previous examples. i attached a mc15 and mc11 version. i didn't realize i could save files as mc11. not sure if you can open either of them. working with this made me notice that some of my previous work may have had an error. i updated some of my formulas. however, i have a lot more work to do, to integrate everything. i'll post them on the other thread, when i get them done.
anthony
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hi luc,
it looks like your custom solver won't accept the square wave with all the extra input variables.
edit; attached is a mc11 file showing the issue. looking at your custom solver, it looks like it wants f to have 3 inputs. the square wave has a lot more inputs than that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The first response I get from the f3 function in your files is:
This is due to the fact that the numeric processor doesn't know x, and complains.
I had explained that LODEsolve is a symbolic-only function. You always have to evaluate it symbolically.
After I've added a symbolic evaluation I get this:
This is due to the fact that the number of cycles is unknown. While the symbolic processor in general can deal with unknown variables, the number of cycles is used by the pulse function in a summation operator. Well, in this case the symbolic processor would like to know how many summations there are. So we can help it by telling. I define nc before using LODEsolve in this definition, and I delete nc from the parameter list of xsym3, gives:
(This expression continues for several pages)
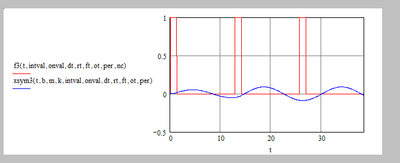
But it can be used. A bit further down you've plotted f3, I put xsym3 along:
.
Now I'll be the first to admit that working symbolically with square wave signals isn't ideal.
I've found no way to define a continuous square wave signal that is acceptable to the symbolic processor.
(With sines and cosines it's easy, they are already known symbolically).
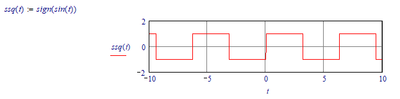
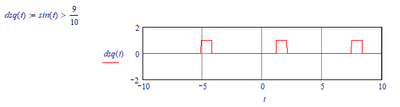
You can define a continuous symmetric square wave as:
but when evaluated symbolically it becomes:
which leads to a Laplace transform of:
And that's not what we wanted.
A continuous asymmetric square wave can be defined with:
But:
So far the only square wave definition that works symbolically, and is Laplace transformable is one that is defined in terms of the Heaviside step functio:
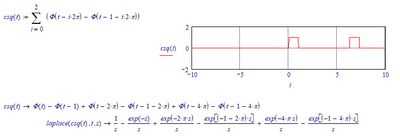
But then you have to define every pulse individually, which can be automated using the summation operator:
but not out to infinity:
So square waves can be used symbolically with a limited number of cycles.
Here's a setup that works (at least in Mathcad 11):
(Again, the expressions above are huge).
Mathcad 11 file is attached.
Success!
Luc
P.S. Be advised that the symbolic process doesn't "know" about units. It doesn't "know" how to convert them etc. like the numeric processor does. At best, it treats them like unknown variables, and if you are careful you can have them cancel out if necessary.
If you want to work with symbolics and units, preferrably first use the symbolics to arrive at a function (with parameters for all your variables that need to carry units) that the numerical processor understands, then call that function with the united variables as parameters. So instead of:
(Note that you do not get t in seconds!)
do:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks luc,
when i open your file in mc15, the xsym definition says 'cannot understand this syntax'.
note; i didn't have the symbolic evaluation on for xsym3 because it just hangs in mc15.
i notice one other thing that might be important. on your custom solver. if i turn on automatic calculation for it, a number of errors show up, within the file. so maybe there is a mc11 to mc15 issue there. it's all way too complex for me to understand. i think i'm just going to abandon the symbolic solve. from what i got for the cosine and sine wave, there was little difference. it did help me find a problem with odesolve. it wasn't running out to the correct tmax. it was short by tstep. i followed the help, but the help wasn't working the way the actual solver is. so i changed one input to odesolve and got the solver to work as expected. so before, the help for state space was messed up. now i find the help for odesolve is messed up too. i think we are having some problems of mc11 to mc15 that are going to make this a nightmare. but i appreciate all the help you provided.