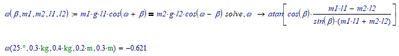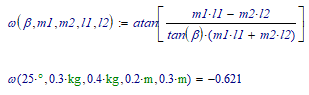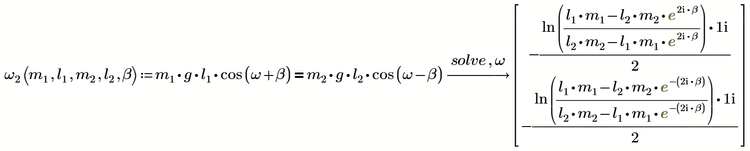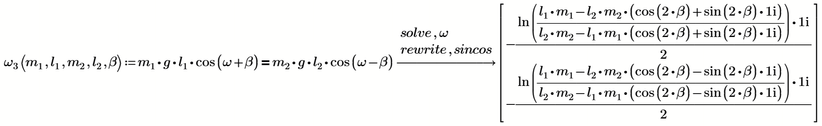Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
"Stan and Olli - Conversion"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"Stan and Olli - Conversion"
A funny comparison and maybe a hidden hint for the next Mathcad Prime version ...
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There's a thinner Stan, found by Mathcad 11 which uses Maple as the symbolic processor:
Which can be further thinned by observing that sin(b)/cos(b)=tan(b), thus:
In Mathcad it has always been hard to control the output of the symbolic processor, and Prime is no exception to that. You may try some symbolic keywords to find a better result in Prime 8. I'd suggest you start with 'simplify'...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There's a thinner Stan, found by Mathcad 11 which uses Maple as the symbolic processor:
Which can be further thinned by observing that sin(b)/cos(b)=tan(b), thus:
In Mathcad it has always been hard to control the output of the symbolic processor, and Prime is no exception to that. You may try some symbolic keywords to find a better result in Prime 8. I'd suggest you start with 'simplify'...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Chapeau, LucMeekes! Thank you for your contribution. Now we have to be careful that Stan doesn't starve to death. Jokes aside - yes, this is an interesting and entertaining game and a nice opportunity to deal with the relationships between the angle functions and the addition theorems ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Prime 6 we can switch between the new symbolic engine (Axiom fork) and the legacy one (muPad).
Here is the result of the "new" engine
and here is muPad (calculating much faster)
or
muPad never was able to live up in quality to Maple (the symbolic engine built in MC11 used by Luc) and when we look closer to the results
we can notice that the second result given by muPad is wrong, it doesn't fulfill the given equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much, Werner_E. I find this variations very interesting. It shows once again that one should always know what he´s doing and estimate if the result is realistic, no matter which CAS system he uses. With a physical counterpart the estimation is usually easier than with pure theory ...