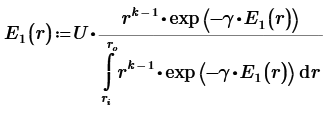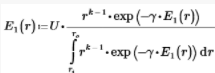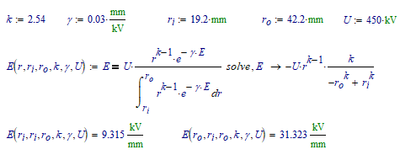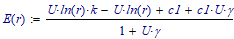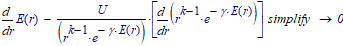Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
solving formula for E-field distribution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
solving formula for E-field distribution
I am trying to solve an equation like:
this one can't be solved analytically and a priori the solve block does not work correctly (in the way I use it.
see attached file
Any idea how to solve this equation
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you,
I have followed your advise and evaluate first the integral and than insert it in the equation for the E-field.
I do not understand why, but this cuts the calculation time significantly and allows the use of a programmed loop.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think that you can iterate and approximate a better solution. Attached is your file (very nice, BTW) with my scribbles on the end. I have only Express, so a solve block won't work for me, but the root function is a nice alternative. Now, the problem with this solution is that it forces a constant value for E, so the integral isn't right. So the first iteration is to replace that constant value in the integral with the solution value. This yields a significantly different curve shape. I did one more iteration (you can continue to iterate, plugging in each successive solution to get the next. Whether or not this produces a better answer or not is beyond my scope.
File in Prime 7.0 attached. Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you,
I tried your proposals in a programmed loop of iterations.
Up to 4 iterations the computing time is acceptable.
For 5 iterations it is getting awful long.
I'll try to build a solver for a Fredholm integral equation of the second kind as described here:
https://mathworld.wolfram.com/FredholmIntegralEquationoftheSecondKind.html
Thanks
Thomas
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
THAE wrote:
Up to 4 iterations the computing time is acceptable.
For 5 iterations it is getting awful long.
I only have Express, so I can't write a program. The attached file extends the idea a few more steps (manually). I noticed that calculation time was extending too. Two suggestions:
- The denominator (the integral over r) is going to be a constant for any E(r). You can cut the evaluation time in half if you calculate it once rather than each time.
- Every OTHER iteration gets closer, the in-between iteration switches shapes. Might be able to shorten calculation time that way too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you,
I have followed your advise and evaluate first the integral and than insert it in the equation for the E-field.
I do not understand why, but this cuts the calculation time significantly and allows the use of a programmed loop.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
THAE wrote
"I do not understand why, but this cuts the calculation time significantly"
The denominator in your basic equation:
will evaluate to the same value for any E(r) since it is the integral over a fixed range. So you can evaluate it once rather than for every value of r in the integration. This eliminates the computation time for all those integrals from the total time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ok, got it, thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Apparently you need a mightier Mathcad to solve this:
The numeric solution of your solve block is close.
The solution is pretty obvious. With E and gamma not dependent on r, you can take the exp(-gamma*E) out of the integral, and cross it off against the same in the numerator. The primitive of r^(k-1) is r^k/k.
Now to eq(1), If you take the derivative of both sides to r, you get a differential equation which may be solvable.
Here's one try:
Solve it to get:
Prove this solves the differential equation:
OK. The next challenge is to determine the integration constant c1.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
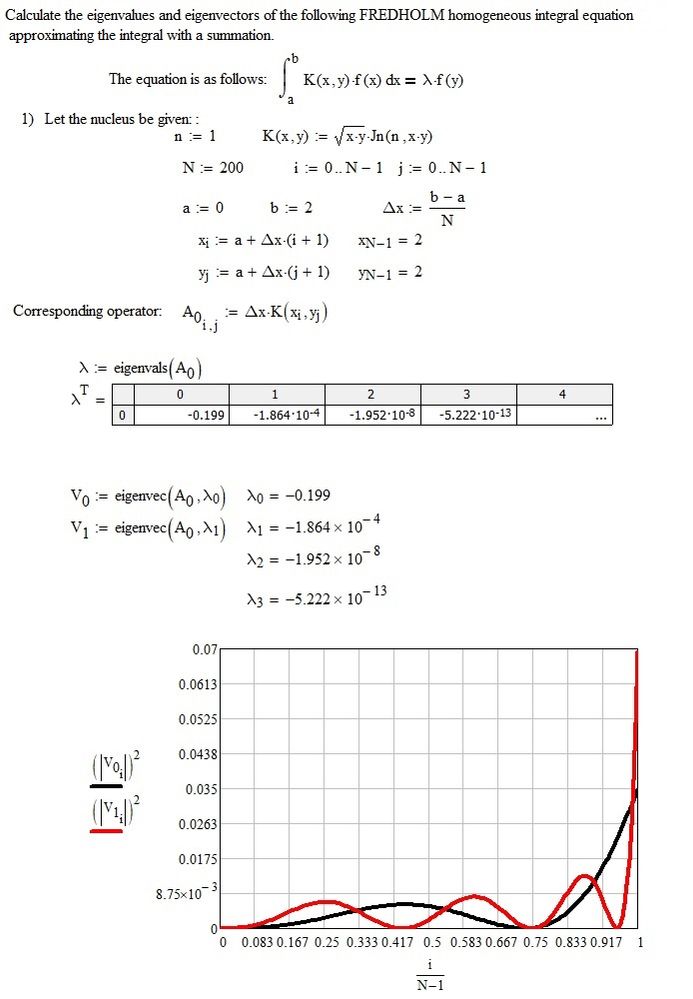
Since, in the equation, the unknown function appears as an argument of the integral, then the equation is an integral equation. You have to see what kind of integral equation it is (for example Fredholm, Volterra, Wiener-Hopf, ...). For a numerical solution you simply have to discretize the integral which becomes a matrix. An eigenvalue equation should come out. Anyway, search the internet for integral equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You might be interested in this elaboration of mine relating to DC power lines, made some time ago, although it does not solve your problem but broadens your knowledge: https://community.ptc.com/t5/PTC-Mathcad/About-DC-Lines-xmcd/m-p/449649?search-action-id=71039740660&search-result-uid=449649.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
An elementary example of a numerical solution of a homogeneous Fredholm equation. The discretized integral equation is transformed into an eigenvalue equation. The eigenvectors corresponding to each eigenvalue are the discretized orthonormalized solutions of the given integral equation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you,
I will try that one and compare to the solution, using iterations, proposed by Fred