Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
symbolic algebra and substitution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
symbolic algebra and substitution
I'm trying to simplify 5 equations by substituting until I have one equation and just a few inputs. The symbolic result is extremely complex and could easily be simplified but no matter what I try, I can't get it to simplify or collect on terms. Further, when I later use the derived equation, the numerical value is incorrect. It is challenging to find where the error is occurring.
Suggestions?
thanks
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the numerical results are different, then the equations are not equivalent.
Are you sure about the 5 initial equations?
By the way, you can perform all the substitutions in one math region:

I included the "simplify" keyword at the end, but it didn't change much from the equation you found.
he result is the same:
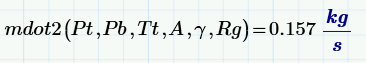
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the numerical results are different, then the equations are not equivalent.
Are you sure about the 5 initial equations?
By the way, you can perform all the substitutions in one math region:

I included the "simplify" keyword at the end, but it didn't change much from the equation you found.
he result is the same:
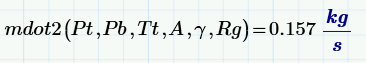
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
After playing a little more, I see that the result should be 0.231, as you noted:

This seems to indicate that there is a bug in Mathcad's symbolics.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark, thanks very much for confirming the problem. I'm certain of the equations and you can see if you use them directly in a solve block or otherwise that the answer should indeed be 0.231. Can you tell me how you did all the substitutions at once? That's pretty handy. It seems that Mathcad prime is quite a bit different than the old mathcad that I'm used to.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I found the source of the problem: All the gammas are defaulting to the built-in constant (Euler's Constant = 0.577...)
You have to manually change each one to have the "variable" label. Once you do that, both equations result in 0.231.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is still something to add...
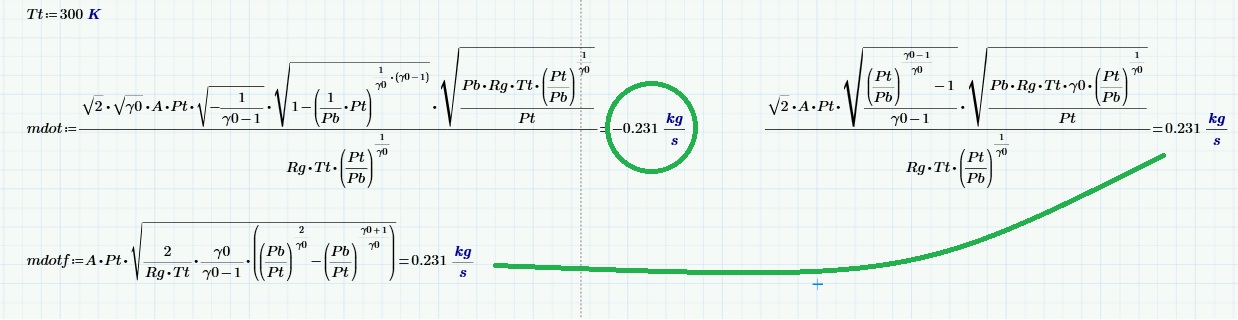
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's a good catch. I assume that is coming from the square root of a negative number since gamma0 is greater than one. do you have any idea how to get the symbolic result to match "mdotf" ?
thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
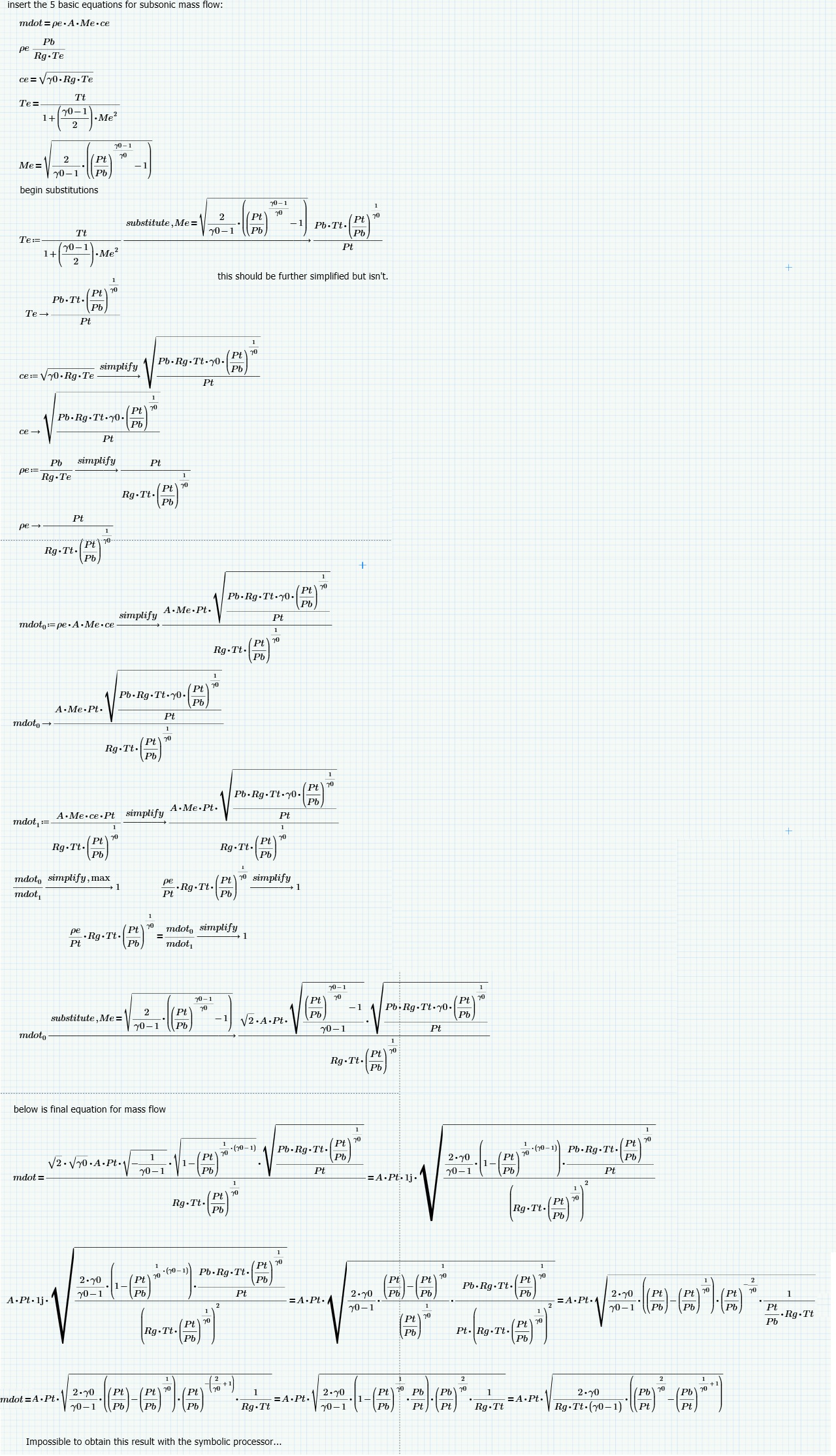
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for checking that Mark. I am now getting the correct numerical value, but a more simplified symbolic result would be nice yet I don't seem to be able to achieve it. Nevertheless, it's nice that you found the source. I am still a bit confused why in symbolic derivation the Euler Constant caused so much grief.
thanks again
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The Euler constant did not cause the problems in the symbolic calculations. It wasn't until the numerical calculation.
If you play with the equations enough, I'm sure you can show that your desired equation (mdotf) is equivalent to Mathcad's derived equation (mdot). Unfortunately, it can be difficult to get Mathcad to display the format of your choice. You can always put something in a text box that says, "it can be shown that eqn1 is equivalent to eqn2."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But you can always (at least try to) subtract two symbolic expressions from each other and show (or hope) that the result is zero. Example to show that (q-p)/q = (1-p/q):

Success!
Luc





