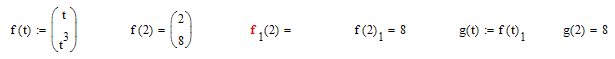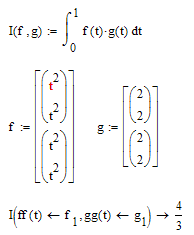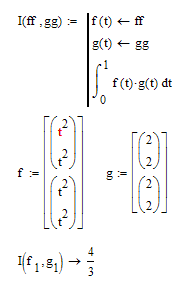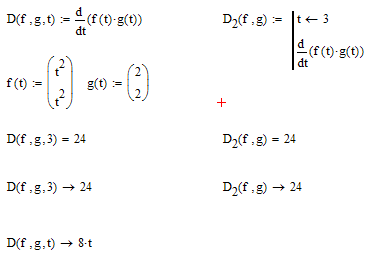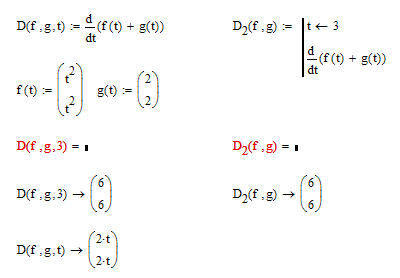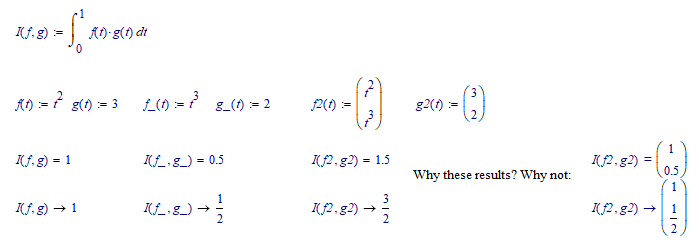Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
vector function integration problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its a long standing wish that Mathcad should be able to deal with vectors of functions but as it seems in vain.
Here is another workaround which does not require you to redefine your integral function. Still unneccessarily awkward.
The problem is: From Mathcads point of view, f is NOT a vector, but the result f(t) is a vector.
So you cannot write f[1(2)= (you get a multiplication sign after f[1), but you can write f(2)[1=
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its a long standing wish that Mathcad should be able to deal with vectors of functions but as it seems in vain.
Here is another workaround which does not require you to redefine your integral function. Still unneccessarily awkward.
The problem is: From Mathcads point of view, f is NOT a vector, but the result f(t) is a vector.
So you cannot write f[1(2)= (you get a multiplication sign after f[1), but you can write f(2)[1=
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a variant of the above which only can be evaluated symbolically
or that way
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much.I understood your way.Do you know how to take derivative (not symbolically) from vector function without iteration through all components of vector function?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ifomenko wrote:
Thank you very much.I understood your way.Do you know how to take derivative (not symbolically) from vector function without iteration through all components of vector function?
Not sure what exactly you mean. Something like in the pic below? Otherwise you would have to provide an example.
Note, that you have to rerly on symbolics if the combined function does not return a scalar, but a vector (thats also the case with the integral)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I mean the following
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess there is no more elegant way as according to thge docs the argument of the derivative operator has to be a scalar valued function. It doesn't work on vector functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is a more elegant (shorter) way:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess I'm lacking some knowledge...
Luc
Ah, found it: f2(t) *g2(t)=3*t^2+2*t^3.