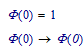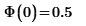Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
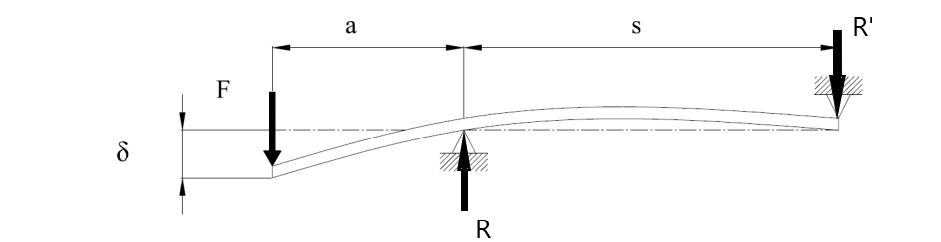
Beam Deflection Plot Question: Macaulay deflection equation has trouble solved by odesolver.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Beam Deflection Plot Question: Macaulay deflection equation has trouble solved by odesolver.
Hello MathCAD People,
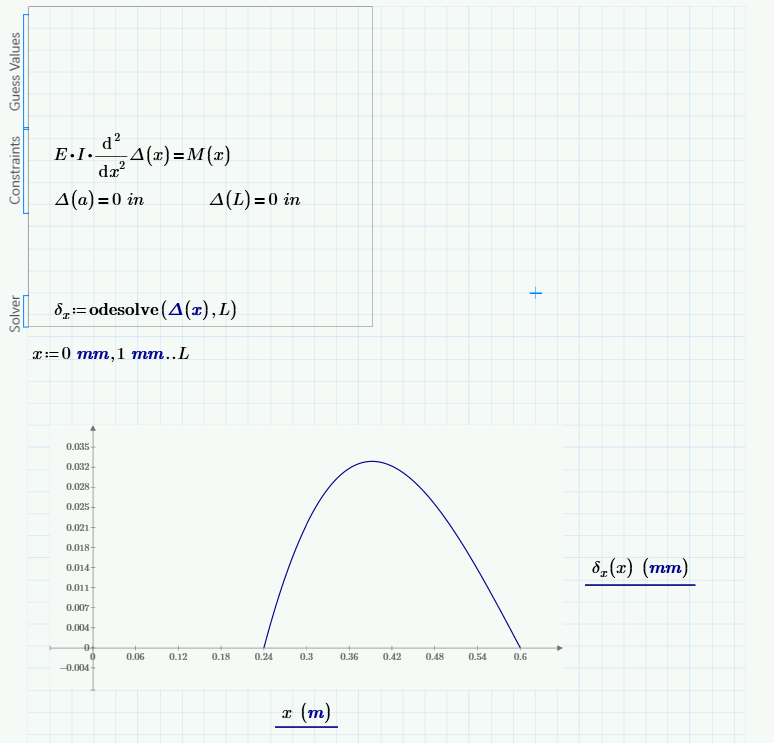
I am working on a shaft redesign project, and I start out with trying to plot the deflection of a more simplified model. I write the momentum function in Macaulay’s method and think plotting a deflection curve using odesolve should be a fast way to figure out where the max deflection happens by solving the differential equation and the boundary conditions. However, the plot just ended up with part of the deflection curve and say the ode function has limited range. Can you guys help resolve the error and get Mathcad plot the full cure?
I really appreciate if you can guide me through this problem, as I really need a math model to validate my simulation results.
Thank you in advance.
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OdeSolve will always use the lowest value in the initial conditions as its starting value and in case of your solve block this is "a".
To get what you are looking for in one go you would have to provide the value for delta.x(0) as initial condition.
You may look up the functions "bvalfit" and especially "sbval" in the help to see if the can be of any help to determine that IC - I lack the experience here as I never have used these functions so far.
https://support.ptc.com/help/mathcad/r6.0/en/index.html#page/PTC_Mathcad_Help%2Fderiving_initial_conditions_for_an_ode.html%23
But Prime allows us to solve from its starting value upwards or downwards. So we can create two separate solve blocks and combine the two functions found.
Prime 6 worksheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
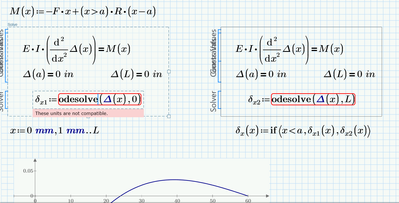
In your call of the odesolve() function, you have Delta and its parameter x labelled as 'units'. I guess they should be 'variables'.
Other than that, some of your variables are labelled 'automatic', some are labelled 'variable'.
I've set all variables to 'variable' but that didn't remove the error message.
Since it's a Prime 6 file, I hope someone smarter than me, can find what (else) is wrong.
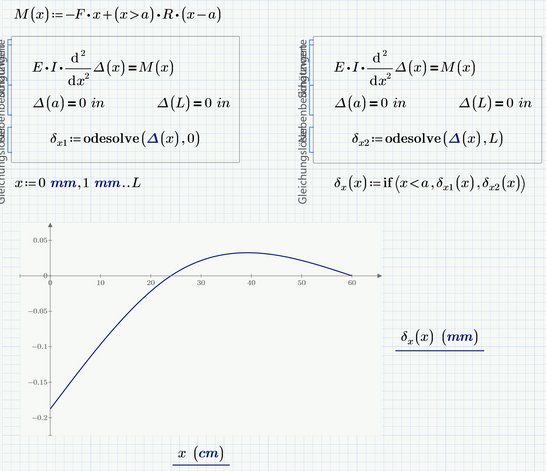
Since your differential equation is relatively simple (a second derivative of a function Delta equals a known expression), here's what I did:
(Note that some of the expressions continue past the line ).
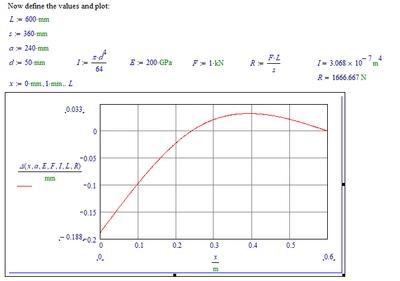
The maximum deflection is 0.033 mm, the minimum is -0.188 mm.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you LucMeekes. I am a newbie to mathcad. Do you mind to tell me what is Φ for? I don't understand its mathematical meaning.
Thanks,
Mito
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@MA_10251892 wrote:
Thank you LucMeekes. I am a newbie to mathcad. Do you mind to tell me what is Φ for? I don't understand its mathematical meaning.
Thanks,
Mito
Phi is the Heaviside step function. It returns 1 for positive arguments and 0 for negative ones. And the implementation in Prime returns 0.5 for the zero argument.
On contrary to an approach with an "if" or a boolean expression as you had chosen, using the heaviside function makes symbolic operations like taking the derivative easier possible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you so much for your information and being supportive for our newbies. I learned a lot today.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The function Φ(x) is the Heaviside step function. It is defined as:
Φ(x) = 0 for x<0
Φ(x) = 1 for x>0
For x=0 the function usually delivers 1, but it may be 1 or 1/2, depending on preference. This may cause problems in some cases.
Mathcad is pretty strict:
it leaves the numerical answer for Φ(0) symbolically.
Prime (4) gives:
I don't know what it delivers symbolically.
But in fact you can do a mathematically sound IF function with Φ.
Knowing/using the fact that 1 means true and 0 means false you'll have
Φ(x-a) means ' x > a ', since if x > a, then x-a is positive, and Φ will return 1 (true)
Φ(a-x) means ' x < a ', the opposite.
The symbolic functions in Mathcad don't accept if statements, so if you need the IF construct in symbolics, you can/have to use the function Φ.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OdeSolve will always use the lowest value in the initial conditions as its starting value and in case of your solve block this is "a".
To get what you are looking for in one go you would have to provide the value for delta.x(0) as initial condition.
You may look up the functions "bvalfit" and especially "sbval" in the help to see if the can be of any help to determine that IC - I lack the experience here as I never have used these functions so far.
https://support.ptc.com/help/mathcad/r6.0/en/index.html#page/PTC_Mathcad_Help%2Fderiving_initial_conditions_for_an_ode.html%23
But Prime allows us to solve from its starting value upwards or downwards. So we can create two separate solve blocks and combine the two functions found.
Prime 6 worksheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you so much for your detailed explanation. I really appreciate your efforts for helping me solve the shaft deflection problem. 😀
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner - Do you know any reason why your worksheet is good with Prime 6, but the odesolve() fail with Prime 7 and Prime 8?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Seems like th community has bn her before:
https://community.ptc.com/t5/Mathcad/Prime-7-and-odesolve/td-p/772661
Work around is to delete units from right side boundary condition.
Also, seems like a bug to me.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting. And I also would call it a bug.
Since I don't value Prime much and therefore don't use it, and since there is a simple trick to make most Prime 7 & 8 worksheets readable for Prime 6, I still haven't found it worth the trouble to get a new licence file generated and install a more recent Prime version. Therefore, I cannot verify the bug myself.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I realize this has been answered, but I set out to solve this the "old fashioned way" without a solve block (using Prime Express), and the result is attached. It can be done!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Fred.