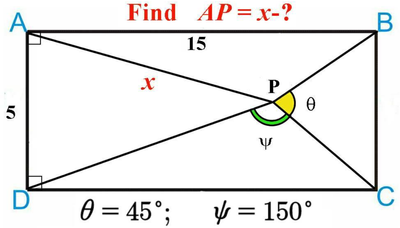
Best solution in Mathcad needed!

[ValeryOchkov]

[LucMeekes]

I've seen more math problems like this...

angles DAB and CDA are 90deg, so we know that AB and CD run in parallel, but the length of CD is not given, and neither is the length of CB. There's no telling if CB runs in parallel of AD.

I doubt if the problem can be solved with just knowing the sum of angles psi and theta. If not, I'm afraid the problem cannot be solved.

Luc

[ValeryOchkov]

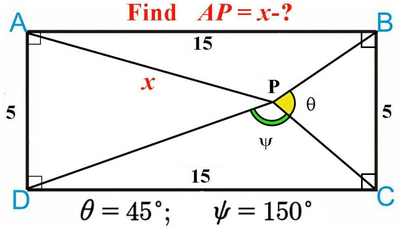
Sorry - more correct picture

[Werner_E]

---

@LucMeekes wrote:

I've seen more math problems like this...

angles DAB and CDA are 90deg, so we know that AB and CD run in parallel, but the length of CD is not given, and neither is the length of CB. There's no telling if CB runs in parallel of AD.

I doubt if the problem can be solved with just knowing the sum of angles psi and theta. If not, I'm afraid the problem cannot be solved.

Luc

---

Hmmm, somewhat sophistic and quibbling, but definitely correct 😉

All we could say with the original specification is that x is in the range from 5 to 15.

In the meantime Valery has added (much too much 😉 additional specifications (one of the additional right angels or one of the additional lengths would suffice).

P.S.: Its a thread by Valery, so it definitely needed an animation 🙂

[LucMeekes]

---

@Werner_E wrote:

---

In the meantime Valery has added (much too much 😉 additional specifications (one of the additional right angels or one of the additional lengths would suffice).

---

Yes,  much too much. Simply stating that ABCD is a rectangle would have sufficed...

---

P.S.: Its a thread by Valery, so it definitely needed an animation 🙂

---

Certainly!

Luc

[-MFra-]

Dear Werner,

despite the tone used with me is that of a discussion between friends, I want to remind you that I am seventy-one years old and that I am not your student.

[Werner_E]

---

@-MFra- wrote:

Dear Werner,

despite the tone used with me is that of a discussion between friends, I want to remind you that I am seventy-one years old and that I am not your student.

---

???

I have no idea what you are talking about!?

And your post was a reply to a post of mine which was a reply to Luc's remark about Valery's sketch missing some specification.

And I can not find a message from myself that would allow to conclude that I treated you as a student (whatever that may mean).

Surely you can not be offended if I call a wrong solution (very cautious anyway) wrong, right?

As I wrote in a reply to Valery my guess that the equations are dependent seems to be wrong and it now looks to me that you will get the correct solution if you replace sin(delta) in your solve block by sin (phi-gamma0).

[-MFra-]

that is my impression when you mention me in your comments.

[Werner_E]

I'm sorry, but you have a wrong impression.
I am glad that you could not call a specific passage in which I was supposedly rude.

[Fred_Kohlhepp]

---

@-MFra- wrote:

Dear Werner,

despite the tone used with me is that of a discussion between friends, I want to remind you that I am seventy-one years old and that I am not your student.

---

This forum is (or used to be) a friendly place to get help, exchange ideas, display humor (look for Valerie's April Fool's submissions); in all the time I've been involved I believe one person has been banned for foul language.

I have been helped, shown my mistakes, and berated for my beliefs.  I consider this a place for interaction.  It's been a long time since my occupation was "student,"  but I usually learn something every time I join.  I believe that if you look at Werner's posts you will find that he generally treats everyone as a colleague, not trying to belittle their efforts.

I encourage you to reexamine the post that you took offense with, consider you're having a discussion rather than listening to a lecture!

[ValeryOchkov]

I am also 71 years old, but I often turn out to be a student of Werner, Luc, Fred, Alan and many other experienced comrades, and I am not offended by this.

The reason may be that for You and Werner English is a non-native language.

[-MFra-]

All right, you're all nice people. 

[ValeryOchkov]

In Russia we show this picture from the famous cartoon and say "Let's live in peace!"

[ValeryOchkov]

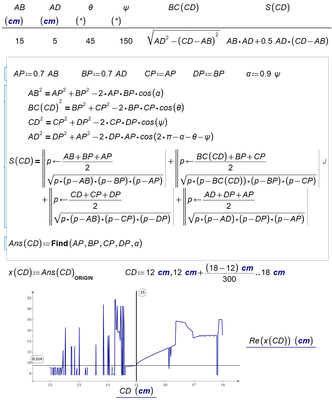
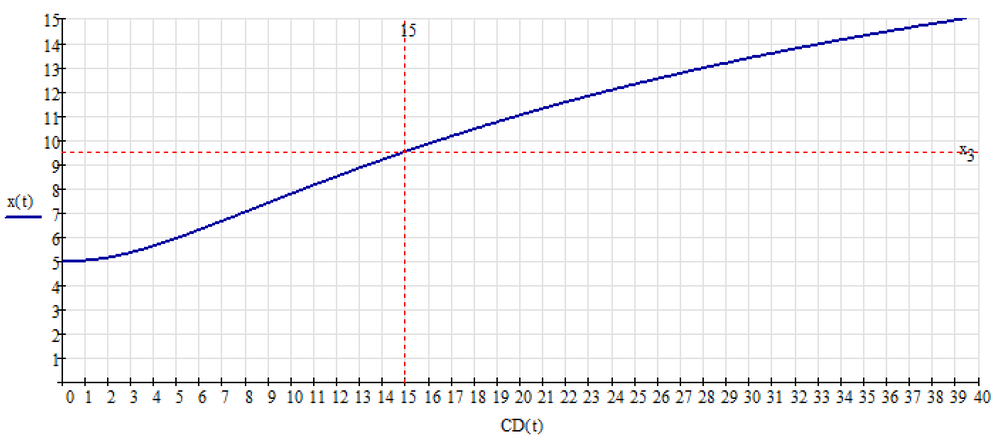
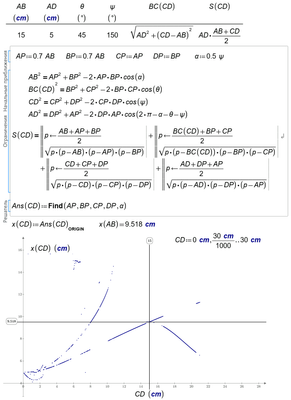
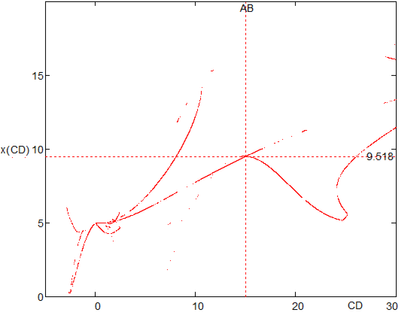
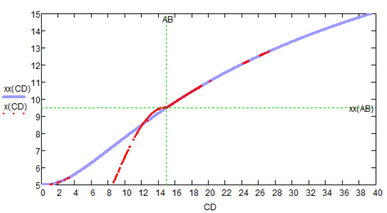
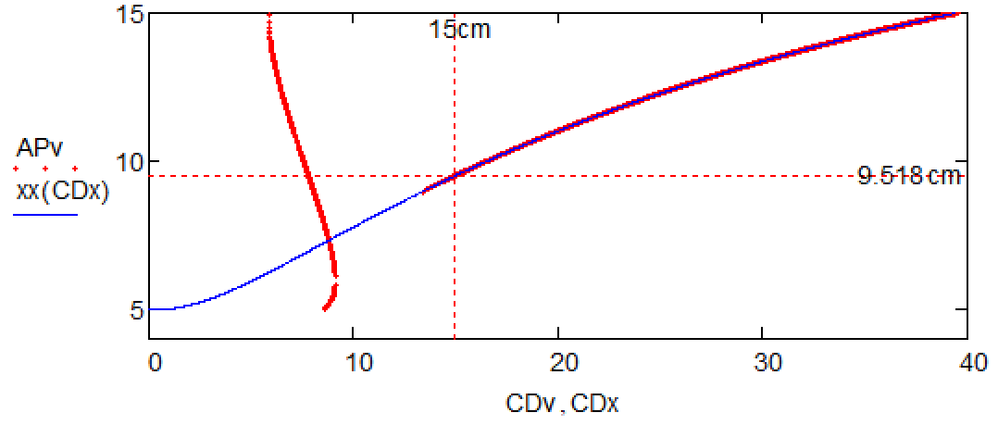
To Werner: Thanks for animation but better to have the x(CD) plot.

To Luc: May be it is not 2D but 3D problem - see please Wire Sculpture

[ValeryOchkov]

---

@LucMeekes wrote:

I've seen more math problems like this...

angles DAB and CDA are 90deg, so we know that AB and CD run in parallel, but the length of CD is not given...

---

My try of numerical solution

[Werner_E]

I modified my animation file and got this:

[ValeryOchkov]

Sorry!

May be this problem has not one but more solutions?

[ValeryOchkov]

Mathcad 15 (the first method in Find):

[Werner_E]

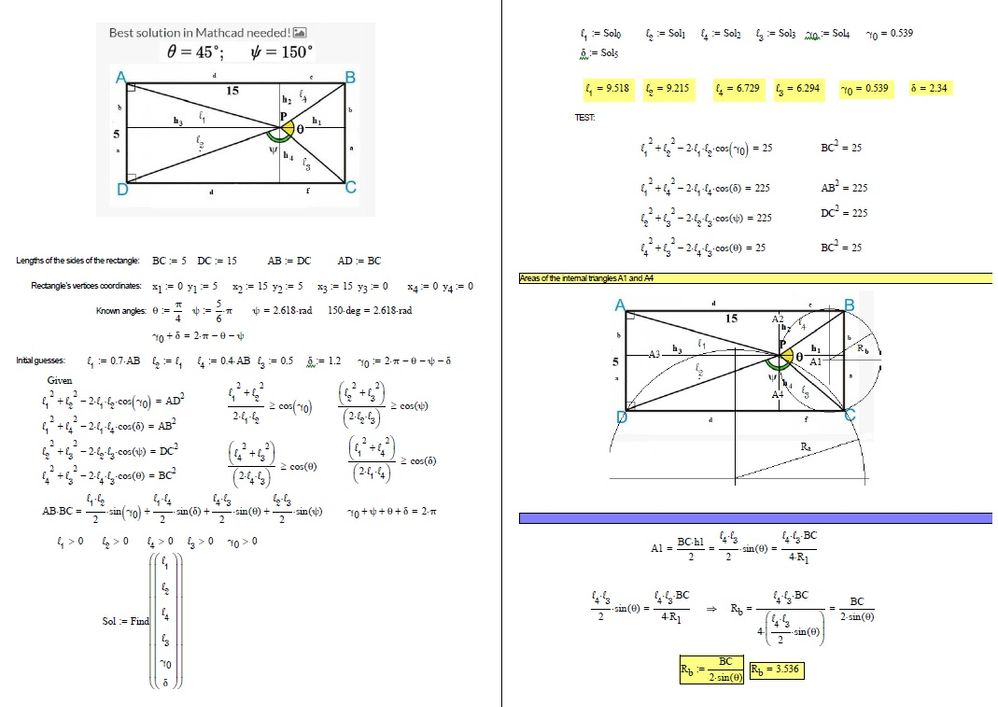
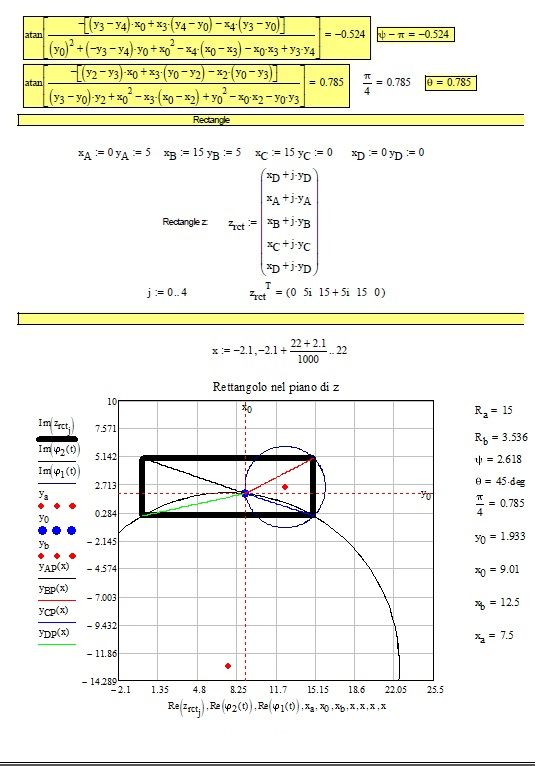
You may add some constraints to get rid of the "multiple solutions" but the results are still unusable in a wide range.

The most important constraint is just that for alpha.

I added a function so you can see what it should look like and where your solve block still fails.

Guess you would need additional constraints to ensure that the point P is INSIDE the rectangle.

I also added another way to compare the areas (the one Francesco had used) - the results are a little bit better but it does not really helps that much.

I added a table at the end of the sheet so you see that your solve block fails sometimes, but most of the time it simply isn't able to come up with a solution at all. Maybe that can help you to improve your solve block.

[DJF]

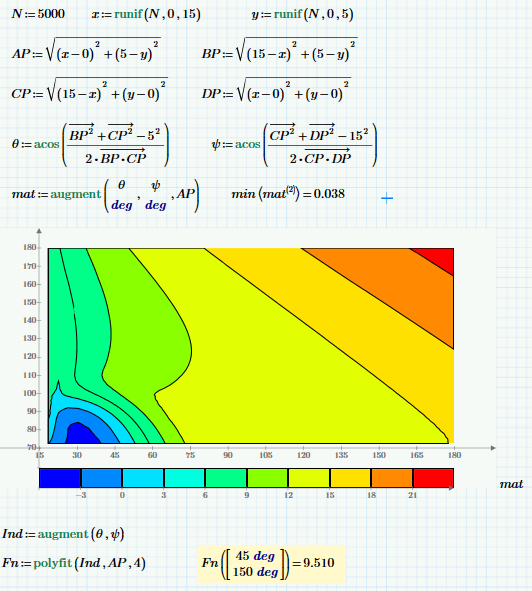
Anyone done a Monte Carlo yet?

Could do a better job with the interpolation, but you get the idea.

[Werner_E]

---

@DJF wrote:

Anyone done a Monte Carlo yet?

---

No, its not necessary as we can derive exact solutions by various methods 😉

---

Could do a better job with the interpolation, but you get the idea.

---

Yes, and I like the idea of your approach. Sure may be useful for other, more complex, problems.

[DJF]

>No, its not necessary  

Well, since Valery didn't define 'best solution' it may be necessary.  We don't know what the scoring system is.  If it's number of individual calculations required I suspect I win (or would with a larger trial sample).

[Werner_E]

---

@DJF wrote:

>No, its not necessary  

Well, since Valery didn't define 'best solution' it may be necessary.  We don't know what the scoring system is.

---

Neither does Valery, I guess 😉

He is known for changing the rules in-midst of a thread, but finally he will usually find the correct solution 🙂

[ValeryOchkov]

And what about this solution?

[Werner_E]

---

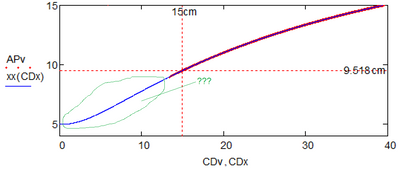
@ValeryOchkov wrote:

And what about this solution?

---

I don't see why you call it a "solution" - you sure see the discrepancy.

I also wonder what you are looking for, what the new goal of this thread should be.

From your post yesterday I thought you were interested to find out why your solve block fails or returns wrong values and how you could fix this. So I tried to provide you with the correct solution to compare with and some tools which might help in finding out whats going on.

Now you post a significantly different sheet which again returns wrong solutions. Why? What is it you want to find at the end?

[ValeryOchkov]

---

@LucMeekes wrote:

I've seen more math problems like this...

angles DAB and CDA are 90deg, so we know that AB and CD run in parallel, but the length of CD is not given, and neither is the length of CB. There's no telling if CB runs in parallel of AD.

I doubt if the problem can be solved with just knowing the sum of angles psi and theta. If not, I'm afraid the problem cannot be solved.

Luc

---

Luc opened pandora's box

[Werner_E]

---

@ValeryOchkov wrote:

---

---

Luc opened pandora's box

---

You happily jumped on the bus, didn't you?

So c'mon - why not close the box again by providing an animation showing the different positions of the points (inside or outside of the quadrilateral) and the various lengths AP when CD runs from 0 to infinity.

[-MFra-]

Update. All that remains is to do the animation:

[ValeryOchkov]

I am tormented by doubts. It seems to me that in this zone there is either no solution or more than one solution!

[Werner_E]

---

@ValeryOchkov wrote:

I am tormented by doubts. It seems to me that in this zone there is either no solution or more than one solution!

---

The reason you get no or multiple results is because your solve block equations seem not to be well conditioned. Guess you need additional or other constraints to make the solve block work OK within the full valid range for CD. You sure know about this problem from your various experiments with different catenaries

.

As long as we demand that P has to be inside the quadrilateral there is exactly one solution (which is also shown by my animation).

You should try to calculate the coordinates of the point P from the solution lengths your methods give you and check, if the point is inside and if two initial angles (you have to calculate them with the coordinates of P) are still correct.

You should see that the second "solutions" you get are not really solutions as they violate either the rule that the point is inside or the angles are wrong.

It should be clear that, if CD changes, P is moving on a circle from D (for CD=0) to B (for CD approx. 39.434) as it has always to be seen at an angle of 165° from the segment BD. There is no solution for P inside the quadrilateral for CD > 39.434.

Create an animation using your calculation methods where CD changes from 0 up to 40 and show the quadrilateral, P and the calculated(!) angles psi and theta.

And .... if you really think that there may be no or two solution for, lets say, CD=9, then take a piece of paper, ruler pencil and compass and manually try to construct a solution. The two circles you have to intersect in doing so will intersect in C and P and I am pretty sure that there will be no third point of intersection and that P will be inside the quadrilateral - so you will end up with a unique solution.

I suggested doing the construction manually with pen and paper because to me that would be just more satisfying than doing it with a CAD or a program like GeoGebra, which you can do, too, of course.

[ValeryOchkov]

Who said that point P must be inside the quadrangle!