Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Hello, World! See my 1-st Prime Animation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
curious thing....
I can open without any problems.
Did you got an error message? If yes, which one?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you use Prime 3.1 or 4?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Aha!
I'm using Prime 4.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And I cannot convert to MP3.
Pretty poor...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Create please pdf.
I will try to convert my Prime Express 4 into full Prime 4.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
here are the pdf's
As to Lagrangesche: after trying to calculate it, it seems for me to be much to complex.
Applying the Newton's Laws is much easier.
Volker
...und mühsam ernährt sich das Eichhörnchen...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
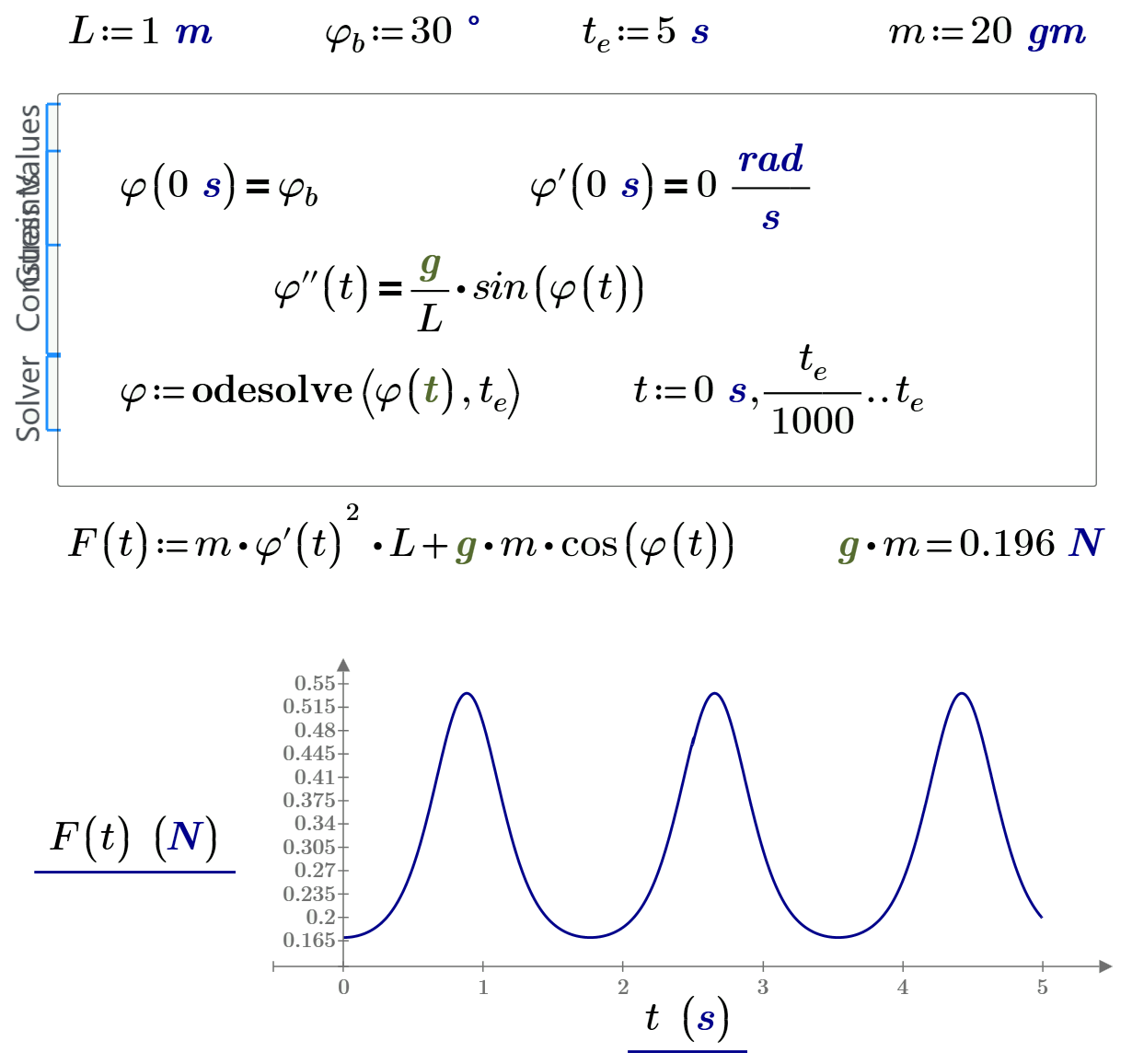
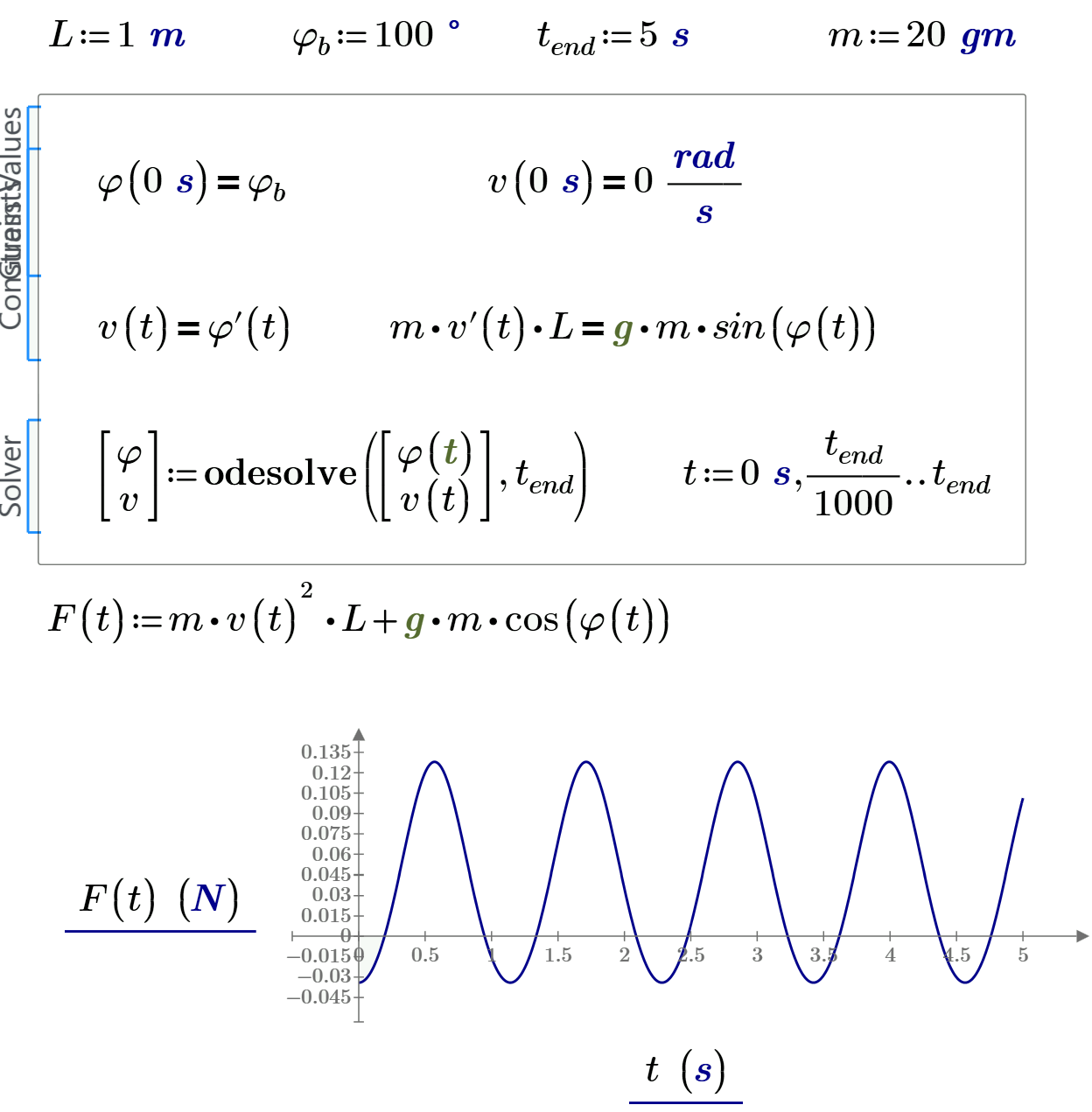
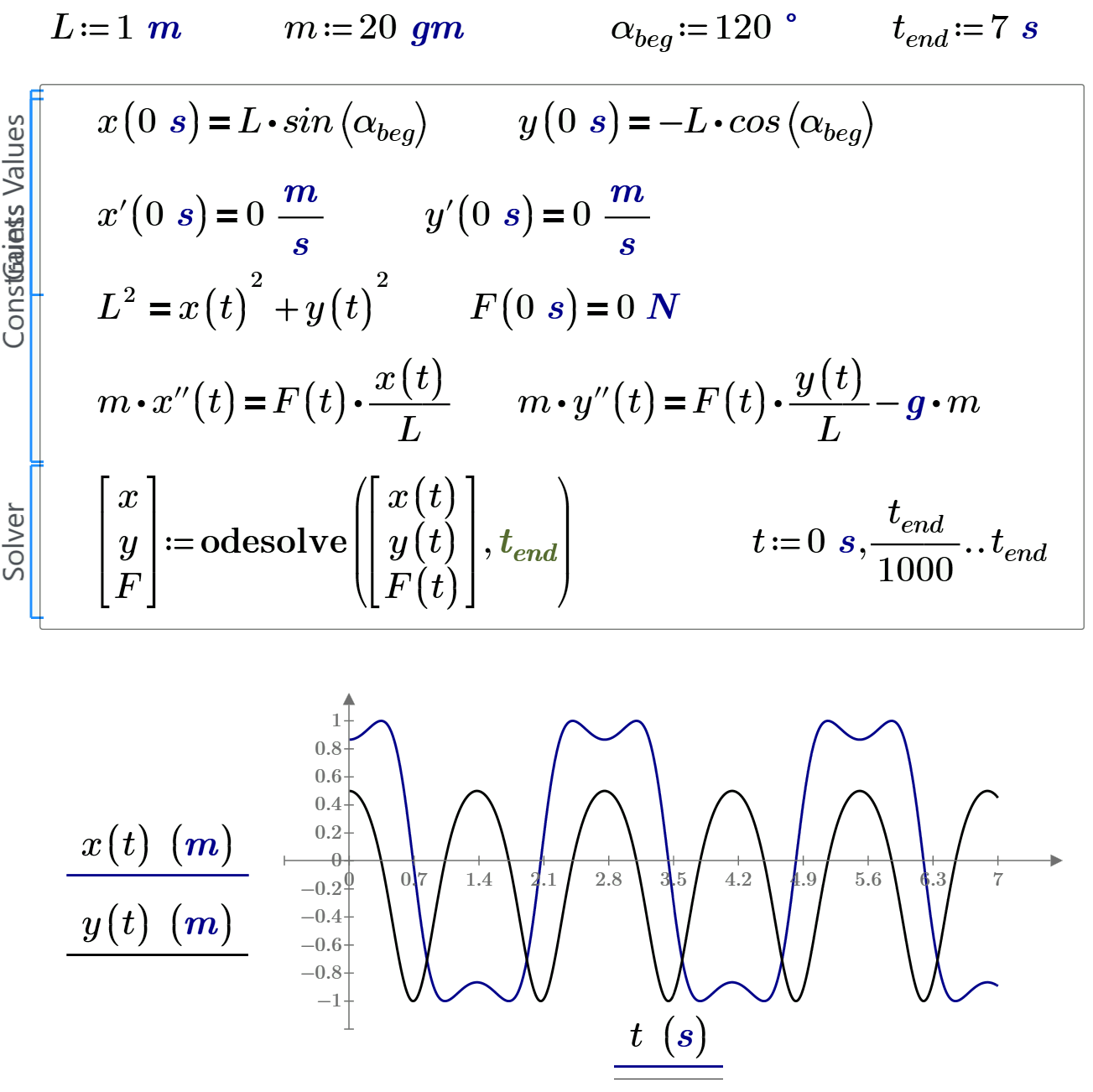
Try it for single pendulum in attach and compare Newton and Lagrange!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
with Lagrangesche: x and y plots are like yours with the Newton.
But my Force-diagramm looks very strange because of the second derivation of simulated x and y.
Please check your Force-Summation: The Inertial forces must point against the moving direction (=Scheinkräfte,Trägheit)! (see handskript sketch, Law of statics)
Edit 01: Files refreshed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery, you're right and I think so too...
The complete Force F1 in the string consists of:
- Zentripetal Force Fz1
- The cosinus-component of the gravitational force, which is in direction of the string.
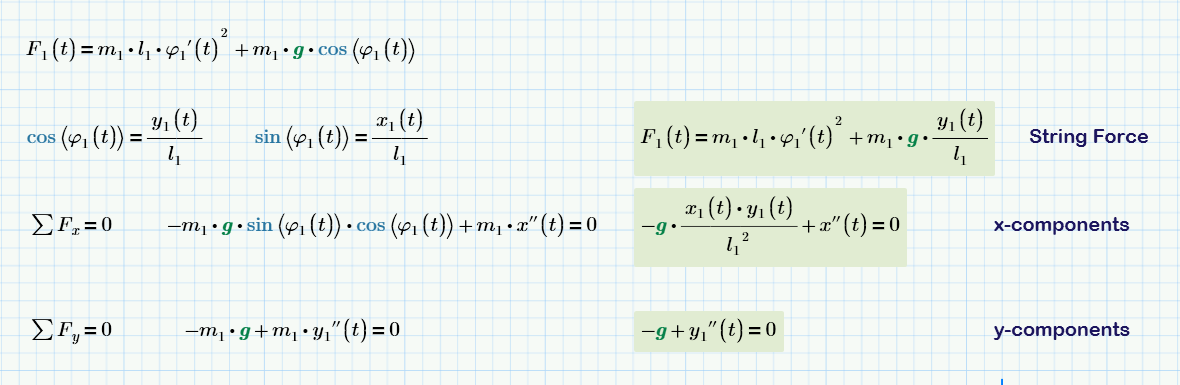
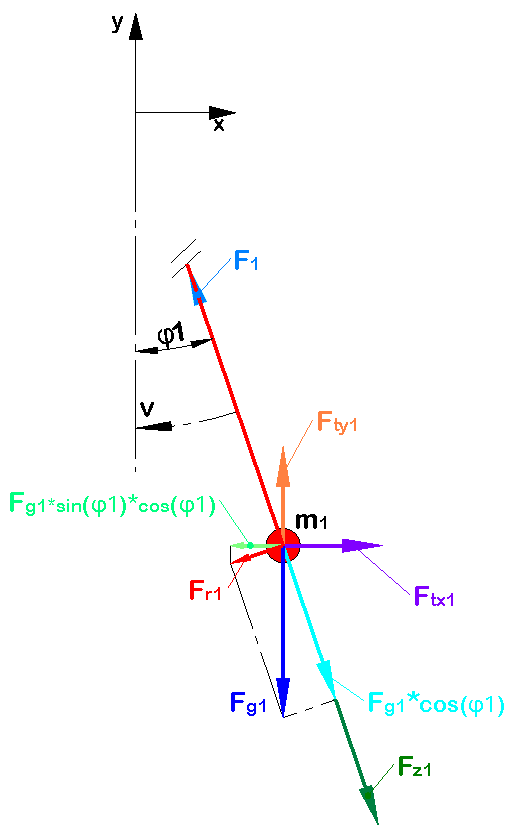
If so, we have to revise all Force components completely in all pendulum modellings!
Heureka?!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok, but it is not Lagrange - it is old good Newton
Lagrange is so Lagrangian mechanics - Wikipedia
Can we find trajectories use not Newton's but Lagrange method?
Is here one reason to use here Newton's but Lagrange method?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
Your equation is wrong.
It has to be for a single pendulum (derived from the Lagrangesche Formalism!):
https://de.wikipedia.org/wiki/Mathematisches_Pendel

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volker Lehner написал(а):
Valery,
Your equation is wrong.
Why! It is same as your one!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No it isn't!
you calculated:
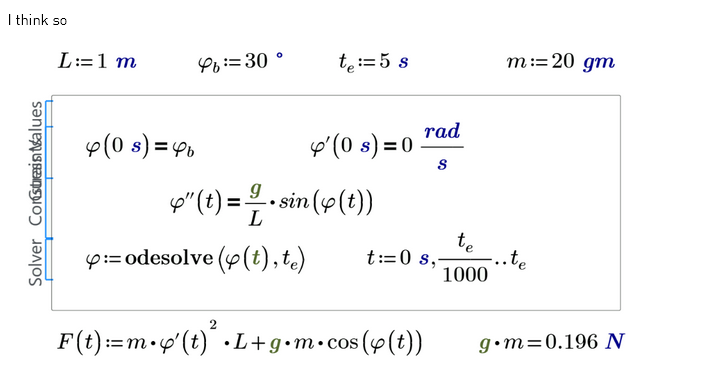
and
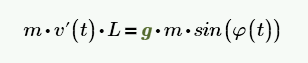
and both are wrong.
right is:
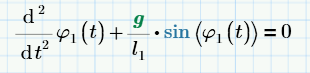
for a single Pendulum.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Compression is a plus, and stretching is a minus.
So in Russia.
Compression is a minus, and stretching is a plus.
So in Germany
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Compression is a minus, and stretching is a plus.
So in Germany
also in Wikipedia and Wikipedia is worldwide.
https://de.wikipedia.org/wiki/Mathematisches_Pendel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I will edit this page of Wiki ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Let end the article so:
Важное замечание.
Решая задачу о тройном маятнике нужно вспомнить об инерциальных и неинерциальных системах отсчета, не только о ньютоновской, но и о лагранжевой и гамильтоновой механике, а также о других тонкостях раздела физики под названием динамика. В настоящее время, почти все физические журналы не принимают к рассмотрению не только статьи с описанием вечных двигателей, но и статьи по динамике с опорой только на ньютоновскую механику. Принцип Лагранжа состоит в том, что траектория материальной точки должна быть такая, чтобы минимизировалась разность между кинетической энергией и потенциальной энергией. Вот мы и закругляемся! Не только в том смысле, что заканчиваем статью, а и в том смысле, что мы возвращаемся к ее началу, где принцип минимизации был применен к задаче статики, а не динамики. Предлагаем читателям решить задачу о тройном маятнике, опираясь не на второй закон Ньютона (см. рис. 16), а на принцип Лагранжа. При этом нужно помнить о том, что этот принцип разрабатывался тогда, когда не было компьютеров с их численными методами решения задач. Нужно также не забывать и о том, что численные методы могут давать большую погрешность, которая может неузнаваемо искажать решение задачи.
Но данная статья не о механике и нюансах решения задач при разных подходах к ним, а о том, как старые не очень сложные задачи можно решать с помощью современных компьютерных средств.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My former goal was to solve the triple pendulum with Lagrangesche.
The equations are simple to define with the difference of the energys Ek and Ep.
But the derivatives of the equations are still to be created.
The next step, to display these extensive equations in a solve block is a very hard way to do-Ok so far, but if i want to simplify these equations, MathCad cannot display the whole equation. Error message: "The symbolic result is too large to display..."
For years I have solved many many mechanical problems with Lagrangesche and every time it was successful.
So the Lagrangesche Formalism is a very good and reliable way to manage such problems.
To solve the double pendulum it was no problem to handle the equations.
To solve the problem of the triple pendulum, the solution variant with Newtonian mechanics was more successful than Lagrange like you showed in an impressive way, Valery.
In this case, I recommend to estimate the usefulness and the effort of different approaches in order to achieve a useful result.
As I said, Lagrange's formalism is quite justified, but it also has limitations in the application of computing.
Best Regards, Volker
...have Fun...and be sucessful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
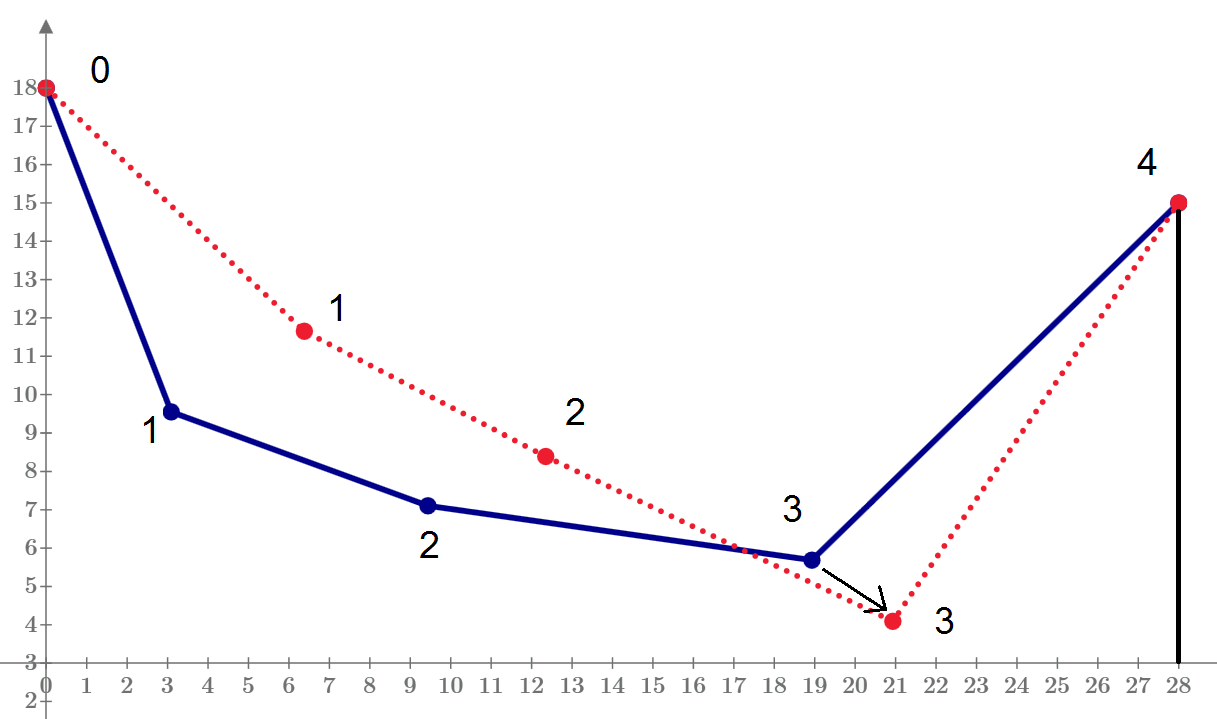
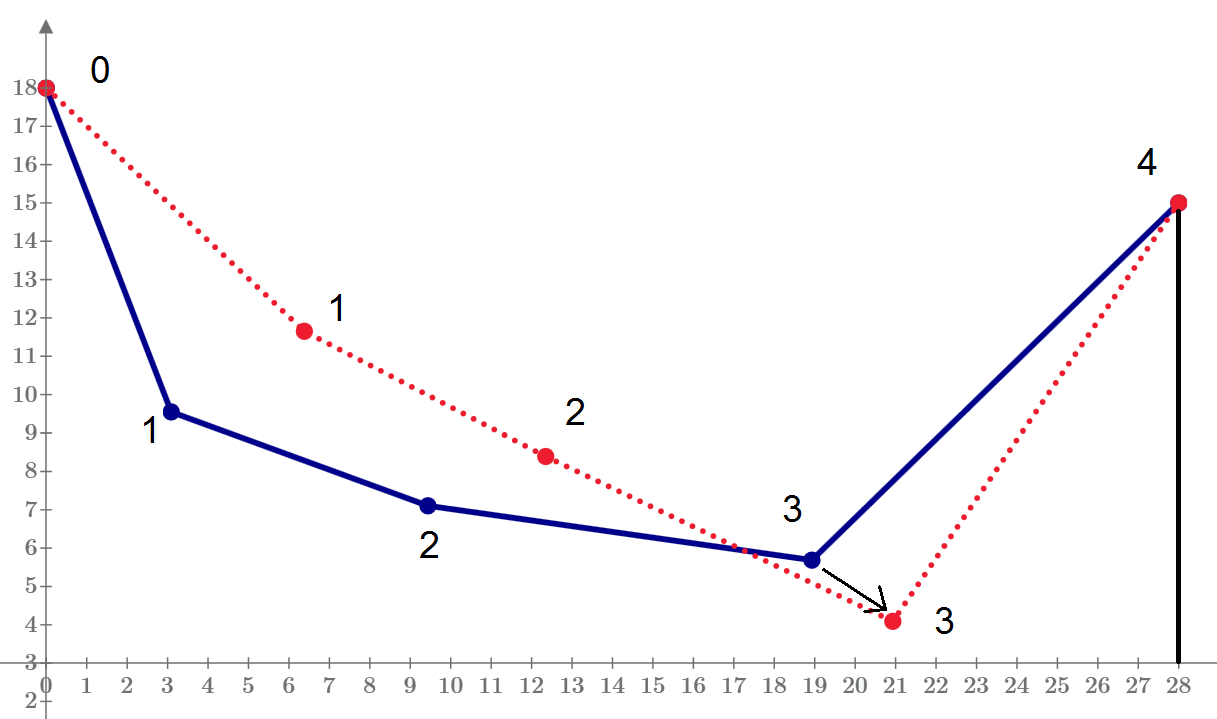
One good idea for new pendulum.
The string 0-1 is not break.
We move by hand the mass #3 to right-down (see the black arrow) and let free it!
How will move point 1, 2 and 3 in time.
It will be new interesting triple pendulum!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
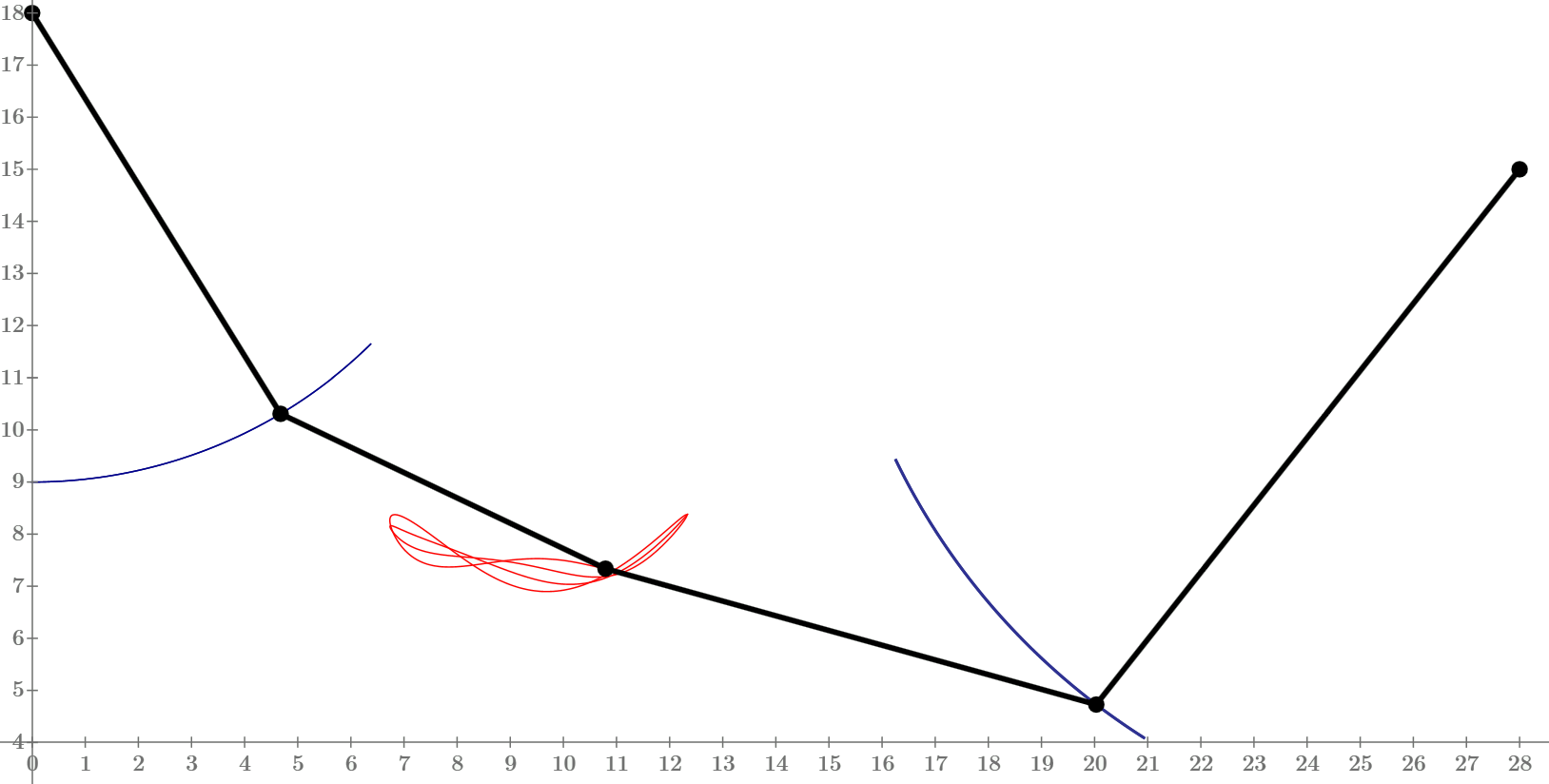
ValeryOchkov написал(а):
One good idea for new pendulum.
The string 0-1 is not break.
We move by hand the mass #3 to right-down (see the black arrow) and let free it!
How will move point 1, 2 and 3 in time.
It will be new interesting triple pendulum!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Animation?
Tomorrow!
Now I go to bet ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice Animation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volker Lehner написал(а):
Nice Animation!
Ich bedanke mich herzlich!
And what about the model? Correct?
Plus in Germany and Russia but minus in Australia ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
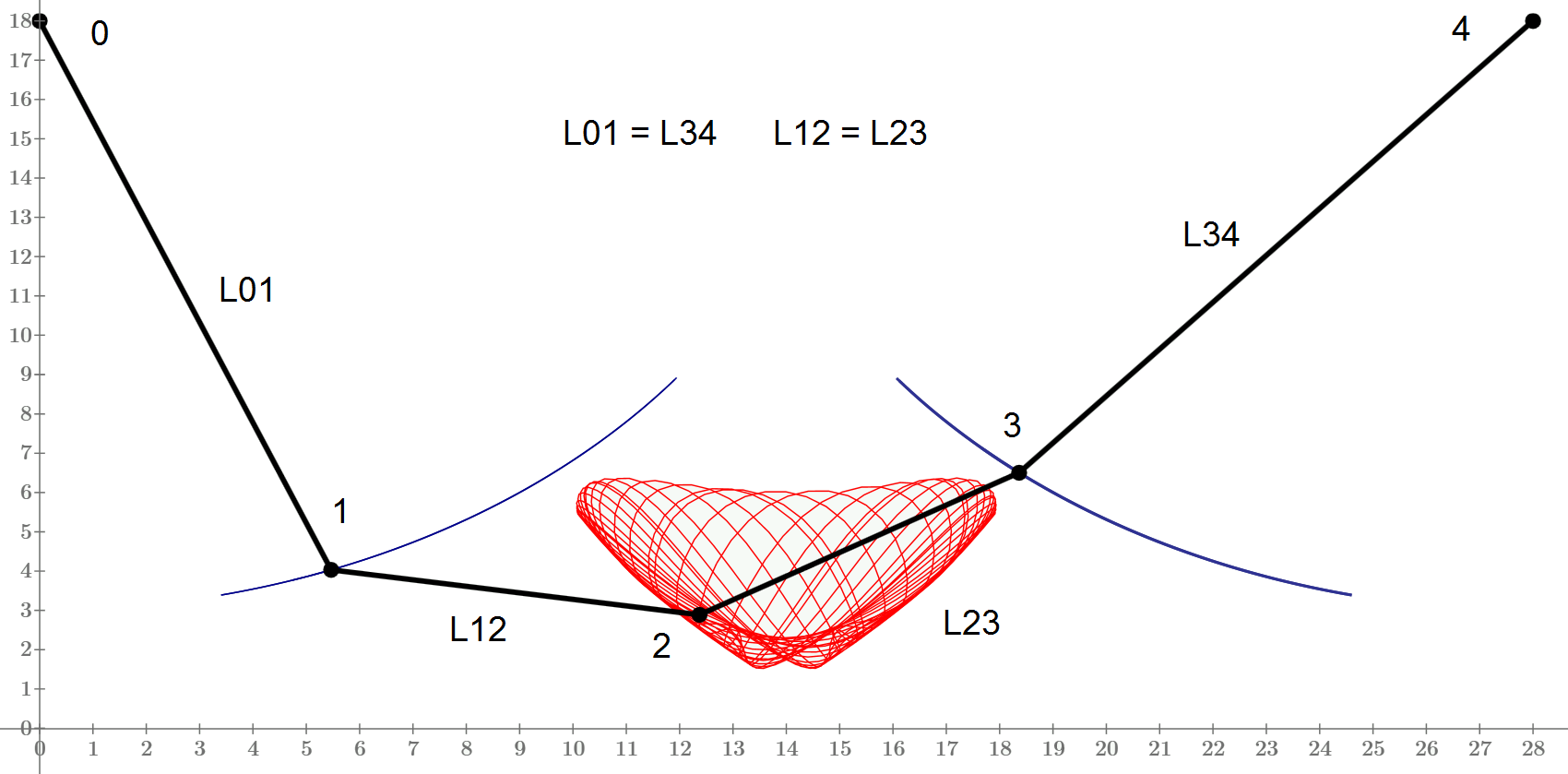
With Hooke's law - not hard links between points, but springs
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
At t>5s we have a static task and go from Odesolve to Find
See please Re: One task with 3 bobs - Forces searching