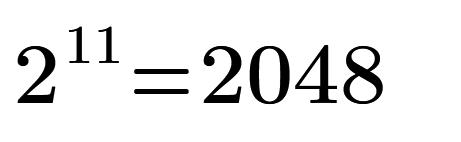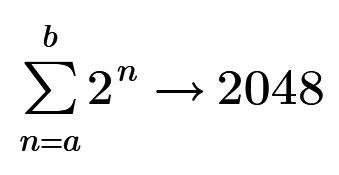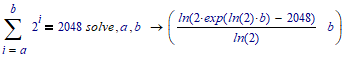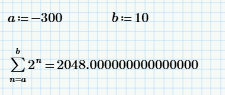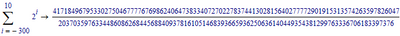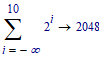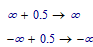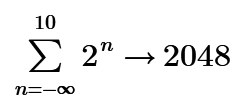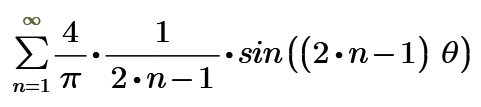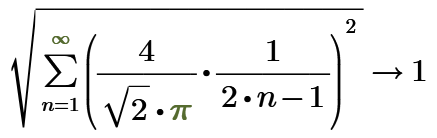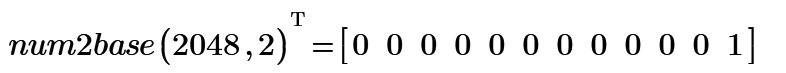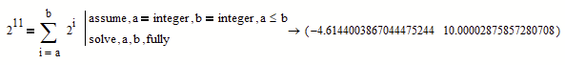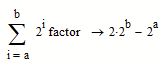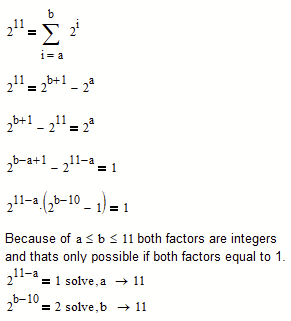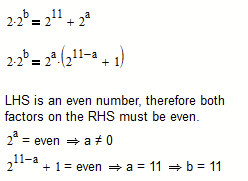How to find the answer?

[ttokoro]

2^11 is 2048. How to find a and b? a and b are integers. 

[StuartBruff]

---

@ttokoro wrote:

2^11 is 2048. How to find a and b? a and b are integers. 

---

AFAIA, the binary expansion of any integer is unique.   

Stuart

[ttokoro]

Prime 7 shows another a and b. 

[StuartBruff]

---

@ttokoro wrote:

Prime 7 shows another a and b. 

---

Given the Puzzles and Games Label, I thought it might.  😈

Stuart

[VladimirN]

Can you upload your worksheet?

[StuartBruff]

---

@VladimirN wrote:

Can you upload your worksheet?

---

Хорошо.   I've modified it slightly to make it more self-contained.

Stuart

Edited to add: Why is it I only notice mistakes *after* I've posted something?  🙂

The original image had the type of the function num2base as returning a String; this was because I copied the function from another worksheet where it made more sense to return a string and I forgot to change the type when I modified the function.   Ridiculum est me!

[LucMeekes]

Hmmm,

Never expected this would happen.

But then, if b is a positive integer <10 then a is complex

for b=10 I get an exception due to trying to take ln(0).

for b=11 , a=11.

for b>11 a is a positive real.

Ah! b=22 gives a=23 (numerically), but:

And with every higher multiple of 11 for b you get closer to a being b+1. for b=1012:

and you don't even need multiples of 11 anymore. For b=1013 the evaluation gives:

But at b=1023 the numerical evaluation fails.

Luc

[StuartBruff]

Neat. 

Something else that occurred to me in my sleep-deprived state early this morning, but which I promptly forgot about until now, was based on one of the many peculiarities of infinities.

(a = -38 does the trick numerically, but I wanted to give the impression of a really large number)

I don't have a symbolic processor to hand to check its result ...

Stuart

[LucMeekes]

Mathcad /Maple will not be fooled:

If you evaluate that numerically, it says 2048,

but that's due to poor (with respect to symbolic) numerical precision,

similar to the numerical results I presented above.

Luc

[StuartBruff · Accepted solution]

---

@LucMeekes wrote:

Mathcad /Maple will not be fooled:

If you evaluate that numerically, it says 2048,

but that's due to poor (with respect to symbolic) numerical precision,

similar to the numerical results I presented above.

Luc

---

Yes, I'd expect that.  However, I do note that Tetsuro specifically mentioned Prime 7.

If, as I implied by my mention of infinities, you plug in -∞ to the expression in Maple you get 2048 symbolically (at least, in Maple Flow you do).

(Mathematica gives "Sum[2^n, {n, -Infinity, 10}] = 2048", as well.  I would hope Mathcad Prime 7 gives the same result?).

Stuart

(Of course, there's the thorny issue of whether -Infinity counts as an integer)

[LucMeekes]

Yep, here you are:

I'm afraid infinity, nor its counterpart -infinity counts as an integer. Small test:

If its equal to itself plus 0.5, then it cannot be an integer:

Luc

[ttokoro]

Many thanks to all mathcsd masters.

My another answer is Stuart's one.

Fourier series of non-sinusoidal wave forms sometimes have infinity Fourier series.

Such as rectangular wave of magnitude 1 shows it as follows.

 

The RMS value is 1. And Mathcad can show it.

And in this case Stuart shows 

This is 1111111111.11111111111111111...

[Werner_E]

> a and b are integers

Mathcad never was able to solve diophantic equations and the symbolics ever so often ignore an "assume, xxx=integer"

You probably are aware thats its quite easy to manually arrive at the unique solution a=b=11.

Given that the sum is

with a<=b<=11, you can do as follows

Somewhat shorter:

But the shortest sure is Stuarts remark about the binary representation of a number being unique.