Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Making a smooth curve in mathcad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Making a smooth curve in mathcad
Hey everyone
Can someone show me how to plot a smooth curve from given data in mathcad?
The problem is attach below
Thank you 🙂
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
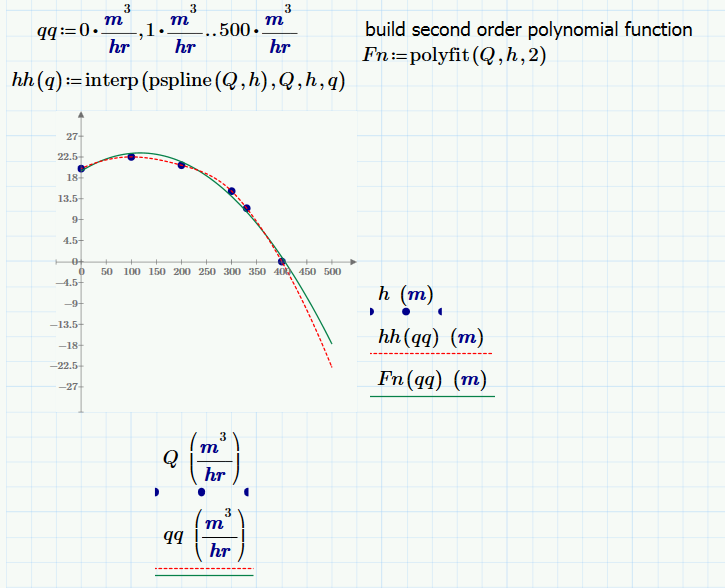
The two answers given (MF and Werner) address splines. A spline will (by definition) pass exactly thru the data points you supply.
Another scenario that often happens produces data that was generated empirically; where the form of the function can be deduced from the physical problem and there is some uncertainty in the measured data. In that case a least squares fit to the data that determines the coefficients of the function may be a better solution:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
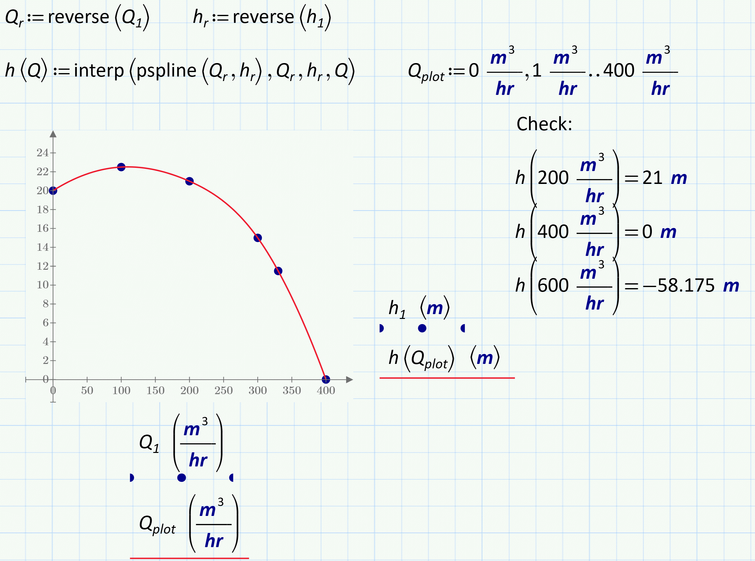
use h1 and Q1 to form a cspline. Use an interpolation of the cspline on a larger number of points.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are some points you have to consider when creating a spline interpolation:
1) The abscissa values must be in ascending order. Thats not the case in your example. So you simply may reverse both vectors Q1 and h1
2) When plotting with units you will have to provide a range variable where you must specify the first, second and last value and aplly units to all three values
3) you may use any of the cubic splines available in Mathcad - lspline, pspline or cspline. Difference is how the ends of the splines are treated - of course all three a cubic splines.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much for the fast reply
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The two answers given (MF and Werner) address splines. A spline will (by definition) pass exactly thru the data points you supply.
Another scenario that often happens produces data that was generated empirically; where the form of the function can be deduced from the physical problem and there is some uncertainty in the measured data. In that case a least squares fit to the data that determines the coefficients of the function may be a better solution: